Numeri di n Cifre con Vincoli Prefissati

Problema

Supponiamo di comporre dei numeri utilizzando soltanto le cifre dell’insieme \(\{1,2,3\}\).
Calcolare il numero totale dei numeri di \(n\) cifre, indicato con \(Z_{n}\), tali che:

• hanno lunghezza n
• iniziano e terminano con la cifra 1
• le cifre adiacenti sono sempre diverse tra loro

Ad esempio se \(n = 4\), le configurazioni possibili sono \(\{1231, 1321\}\).

Suggerimento
Analizzare la terzultima cifra del numero. Distinguere i casi in cui la cifra è uguale a \(1\), oppure è uguale a \(2,3\).

Prima soluzione con metodi elementari

Sia data una disposizione delle cifre:

\[ x = x_{1} x_{2} \cdots x_{n-2} x_{n-1} x_{n} \]

Per le ipotesi del problema abbiamo \(x_{1}=x_{n}=1\).
Per dimostrare il teorema calcoliamo la percentuale del numero delle cifre uguali a 1 a partire dalla seconda posizione, man mano che costruiamo l’albero delle possibili configurazioni.

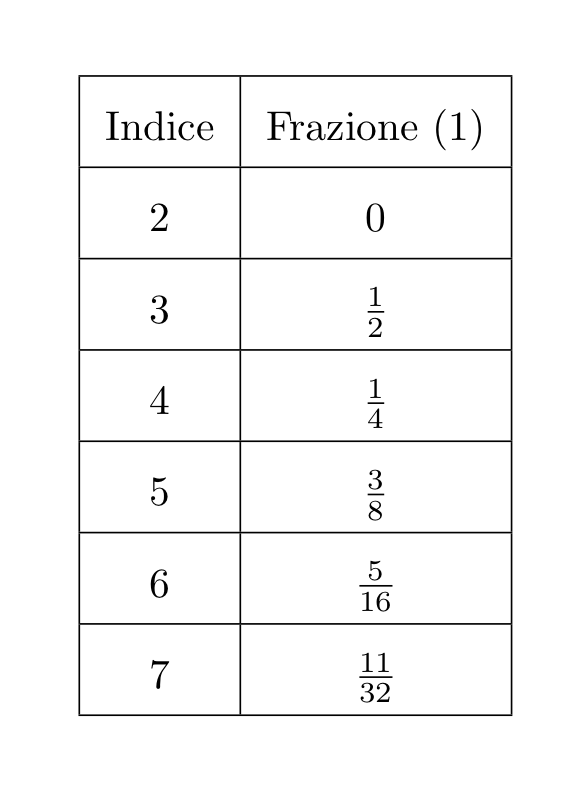
Come si può notare, la percentuale del numero delle cifre uguali ad 1, indicata con \(a_{k}\) con \(k > 2\), in funzione della posizione \(k\) della cifra, è data dalla seguente formula:

\[ a_{k} = (\frac{1}{3}) \cdot (\frac {2^{k-2} + (-1)^{k-1}}{2^{k-2}}) \]

Se prendiamo la posizione \(k=n-2\), cioè la terzultima cifra del numero, allora abbiamo:

\[ a_{n-2} = (\frac{1}{3}) \cdot (\frac {2^{n-4} + (-1)^{n-1}}{2^{n-4}}) \]

La posizione con indice \(n-2\) ha un ruolo cruciale; infatti possiamo distinguere due casi disgiunti:
a) \(x_{n-2} = 1\)
b) \(x_{n-2} = 2\) oppure \(x_{n-2}=3\)

Nel primo caso, poiché l’ultima cifra \(x_{n} = 1\), abbiamo due possibili scelte, \(x_{n-1}= 2\) oppure \(x_{n-1}=3\).
Nel secondo caso invece per la cifra \(x_{n-1}\) non c’è più possibilità di scelta: infatti deve essere \(2\) se la precedente è \(3\), oppure deve essere \(3\) se la precedente è \(2\).
Inoltre il numero totale delle configurazioni fino alla posizione \(n-2\) compresa è uguale a \(2^{n-3}\), in quanto in ognuna delle posizione abbiamo a disposizione due scelte distinte.
Quindi per calcolare il numero totale delle configurazioni che rispettano i vincoli del problema dobbiamo sommare quelle che hanno la cifra 1 nella posizione \(n-2\) con quelle che hanno le cifre \(2,3\). Nel primo caso abbiano:

\[ N_{1}= 2 \cdot 2^{n-3} \cdot a_{n-2} \]

Nel secondo caso abbiamo:

\[ N_{23} = 2^{n-3} \cdot (1 – a_{n-2}) \]

Sommando i due valori e semplificando, si trova finalmente che il numero cercato, \(Z_{n}=N_{1}+N_{23}\) è:

\[ Z_{n}=(\frac{1}{3}) \cdot (2^{n-1} + 2 \cdot (-1)^{n-1}) \]

Seconda soluzione

Questa soluzione consiste nello scrivere l’equazione lineare di ricorrenza del valore \(Z_{n}\) e quindi risolvere con i metodi standard delle equazioni alle differenze finite. Per uno studio approfondito della matematica discreta e in particolare delle equazioni alle differenze finite si può vedere il testo ^[1].
In base alle considerazioni fatte in precedenza, non è difficile ottenere l’equazione di ricorrenza:

\[ Z_{n} = Z_{n-1} + 2\cdot Z_{n-2} \]

Questa equazione lineare del secondo ordine può essere risolta con i metodi standard, risolvendo l’equazione caratteristica:

\[ \lambda ^2 – \lambda – 2 = 0 \]

Le radici sono: \(2, -1\).
Poiché le due radici sono distinte, la soluzione generale è:

\[ Z_{n}= h \cdot 2^{n} + k \cdot (-1)^{n} \]

I valori delle costanti h,k vengono determinati con le condizioni iniziali del problema: \(Z_{2}=0\) e \(Z_{3}=2\).

Soluzione:

\[ Z_{n}=(\frac{1}{3}) \cdot (2^{n-1} + 2 \cdot (-1)^{n-1}) \]

---

Bibliografia

^[1]Seymour Lipschutz – Discrete Mathematics (McGraw-Hill)