Le Parentesi di un Prodotto e i Numeri di Catalan

Problema

Siano dati n numeri \(x_{1},x_{2}, \cdots x_{n}\), nell’ordine prescritto. Calcolare il numero \(C_{n}\) dei possibili modi di posizionare le parentesi per moltiplicare il prodotto degli n numeri, senza modificare l’ordine dato.

Suggerimento
Se \(n=2\) abbiamo un solo caso: \((x_{1} x_{2})\).
se \(n=3\) abbiamo i seguenti casi: \(((x_{1} x_{2})x_{3}), (x_{1}(x_{2}x_{3}))\).
Se \(n=4\) abbiamo i seguenti casi:
\((((x_{1}x_{2})x_{3})x_{4})\), \(((x_{1}(x_{2}x_{3}))x_{4})\), \(((x_{1}x_{2})(x_{3}x_{4}))\),
\((x_{1}((x_{2}x_{3})x_{4}))\), e \((x_{1}(x_{2}(x_{3}x_{4})))\).

Può essere utile anche determinare l’equazione di ricorrenza per \(C_{n}\). Non è difficile infatti dimostrare che l’equazione è la seguente:

\[ C_{n} = C_{1}\cdot C_{n-1} + C_{2}\cdot C_{n-2} + \cdots + C_{n-1}\cdot C_{1} \]

valida per \(n \ge 2\). Abbiano posto le seguenti condizioni iniziali: \(C_{0}=0 \) e \(C_{1}=1\).

Soluzione 1

Possiamo tradurre il nostro problema in un problema simile di passeggiata aleatoria molto conosciuto.
Esaminiamo ad esempio il caso \(n=4\); abbiamo le seguenti possibilità:
\((((x_{1}x_{2})x_{3})x_{4})\), \(((x_{1}(x_{2}x_{3}))x_{4})\), \(((x_{1}x_{2})(x_{3}x_{4}))\),
\((x_{1}((x_{2}x_{3})x_{4}))\), e \((x_{1}(x_{2}(x_{3}x_{4})))\).

Se trascuriamo le parentesi aperte, notiamo che in ogni stringa il numero delle parentesi chiuse è uguale a \(n-1\). Inoltre il primo elemento di una stringa è sempre una cifra e l’ultimo una parentesi chiusa.
Possiamo rappresentare una qualsiasi stringa, ad esempio la \(((x_{1}x_{2})(x_{3}x_{4}))\), trascurando le parentesi aperte, con il diagramma seguente:

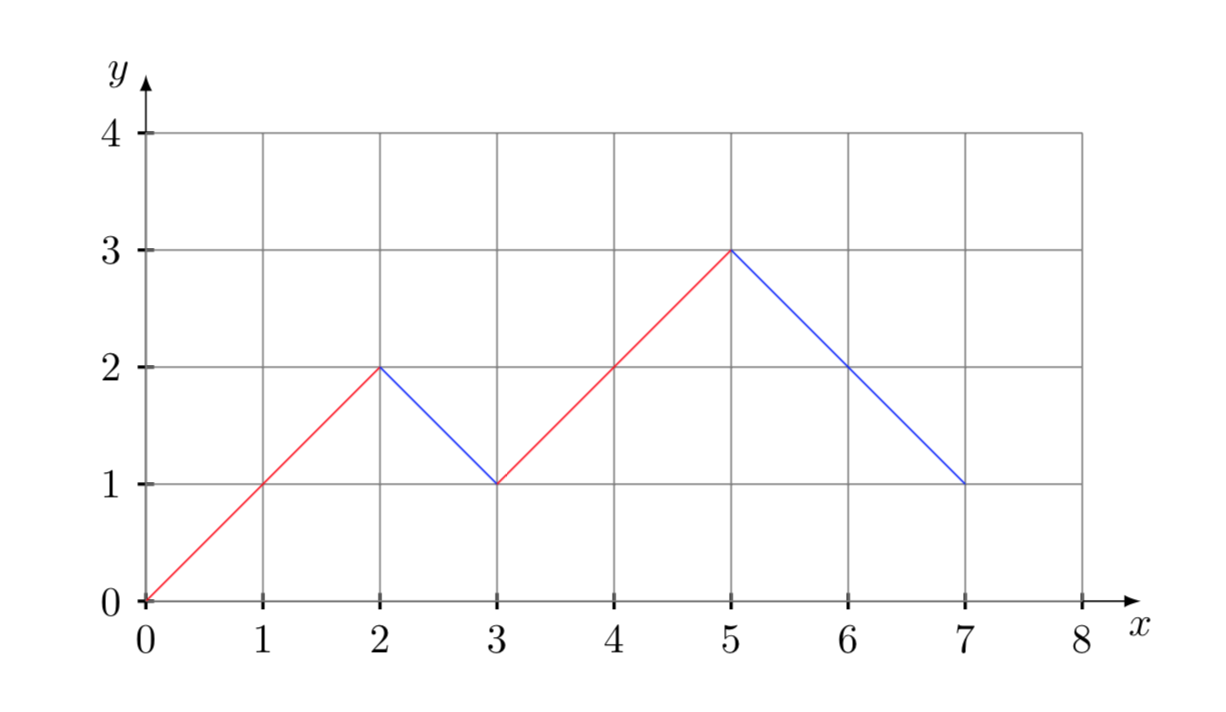
Ogni volta che incontriamo una cifra ci spostiamo verso l’alto, mentre se incontriamo una parentesi chiusa ci spostiamo verso il basso. I cammini validi sono quelli che, partendo dal punto di coordinate (0,0) non toccano o attraversano l’asse delle ascisse, e terminano nel punto di coordinate (2n-1,1).
Di fatto il problema è equivalente a quello di calcolare il numero di questi cammini. Si tratta di un classico problema di calcolo combinatorio e probabilità ampiamente conosciuto e risolto. Il numero dei cammini ricercato si trova sottraendo al numero dei cammini totali il numero dei cammini che toccano o attraversano l’asse delle ascisse.
In generale il numero totale dei cammini che vanno dal punto(0,0) al punto (n,x) è uguale a \(\binom{n}{\frac{n+x}{2}}\).
Applicando questa formula nel nostro caso troviamo che il numero totale dei cammini dal punto (1,1) al punto (2n-1,1) è uguale a:

\[ T_{n} = \binom{2n – 2}{n-1} \]

Per calcolare il numero dei cammini che vanno dal punto (1,1) al punto (2n-1,1) e che toccano o attraversano l’asse delle ascisse, applichiamo il principio di riflessione illustrato nel seguente diagramma (vedere Feller, pag. 72).

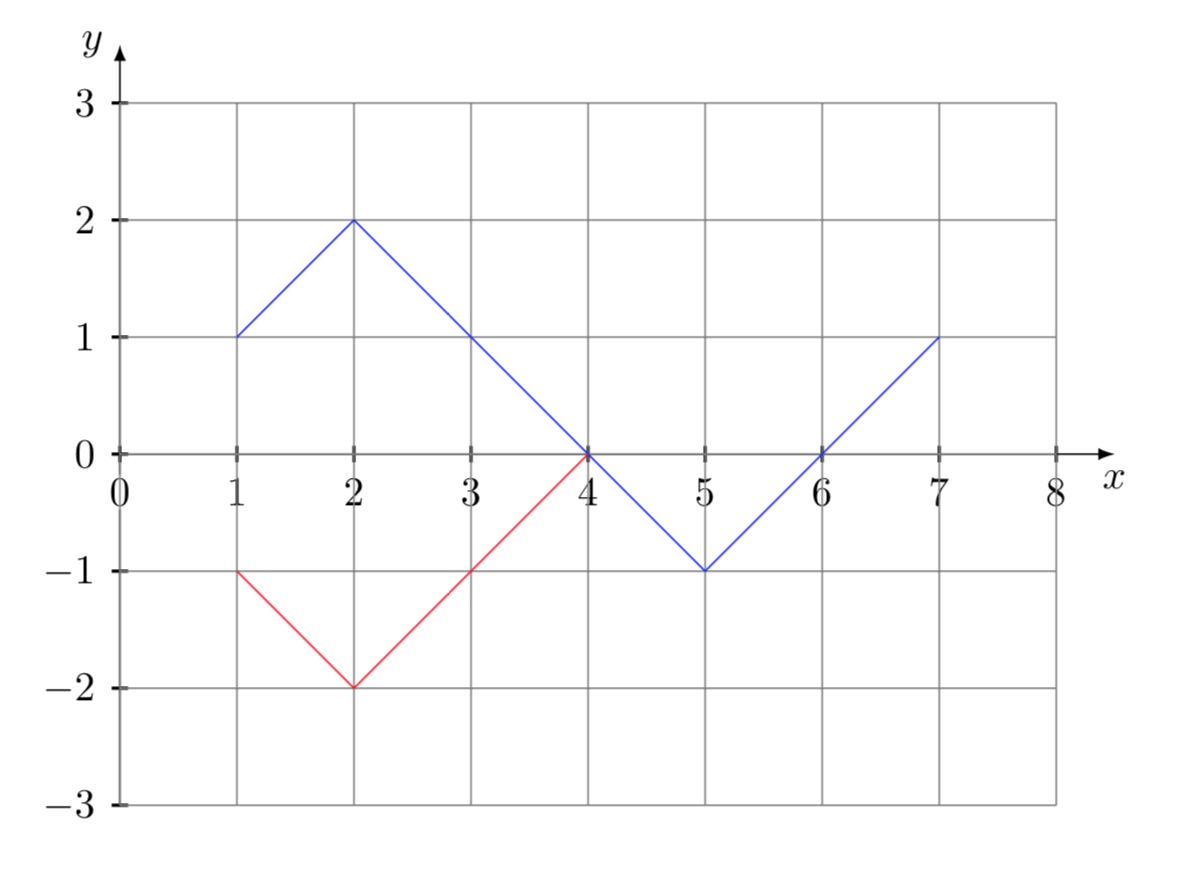
Come si vede chiaramente dal diagramma, il numero dei cammini dal punto (1,1) al punto (2n-1,1) che toccano o attraversano l’asse delle ascisse, indicato con \(S_{n}\), è uguale al numero totale dei cammini che vanno dal punto (1,-1) al punto (2n-1,1). Quindi, applicando la formula generale sopra esposta, abbiamo:

\[ S_{n} = \binom{2n – 2}{n} \]

Facendo la differenza otteniamo il risultato cercato:

\[ C_{n} = T_{n} – S_{n} = \frac{\binom{2n – 2}{n-1}}{n} \]

I numeri \(C_{n} \) sono chiamati numeri di Catalan, in onore del matematico belga Catalan(1814–1894), e intervengono in molti problemi di matematica discreta.
Per un approfondimento di questi problemi vedere ad esempio ^[1] e ^[2].
Alcuni testi cambiano le condizioni iniziali e il numero di Catalan di ordine \(n\) è indicato con il valore \(\frac{\binom{2n}{n}}{n+1}\), che corrisponde al nostro \(C_{n+1}\).

Soluzione 2 (mediante le funzioni generatrici)

Data la funzione generatrice dei numeri \(C_{n}\):

\[ F(x) = C_{0} + C_{1}\cdot x + C_{2} \cdot x^2 + \cdots \]

Se calcoliamo il quadrato della \(F(x)\), abbiamo:

\[ F(x)^2 = C_{2} \cdot x^2 + C_{3} \cdot x^3 + \cdots \]

in virtù dell’equazione di ricorrenza soddisfatta dai coefficienti \(C_{n}\). Con semplici passaggi possiamo scrivere l’equazione funzionale soddisfatta dalla funzione \(F(X)\):

\[ F(X)^2 – F(x) + x = 0 \]

Risolviamo questa equazione di secondo grado nella variabile \(F(x)\), trattando \(x\) come una costante. Tenendo conto delle condizioni iniziali del problema, si scarta una delle due soluzioni e si accetta l’altra:

\[ F(x) = \frac{1- \sqrt{1- 4 \cdot x}}{2} \]

A questo punto troviamo lo sviluppo in serie Taylor di questa funzione, utilizzano lo sviluppo binomiale di Newton, valido per \(|x| < 1\) e per ogni numero reale \(\alpha\):

\[ (1+x)^\alpha = 1 + \alpha x + \frac{\alpha \cdot (\alpha -1)x^2 }{2!}+ \frac{\alpha \cdot (\alpha -1)(\alpha -2)x^2}{3!}+ \cdots= \sum_{k=0}^{\infty}{\binom{\alpha}{k} x^k} \]

Facendo i calcoli troviamo infine la soluzione:

\[ C_{n} = \frac{\binom{2n – 2}{n-1}}{n} \]

---

Bibliografia

^[1]William Feller – An introduction to Probability Theory and its applications, Vol. I (Wiley)

^[2]Donald Knuth – The Art of Computer Programming: Fundamental Algorithms, Vol. I (Addison Wesley)