Tre Problemi di Geometria di Massimo e Minimo

Esercizio 1

Un quadrato e un triangolo hanno la stessa area. Quale dei due ha il perimetro maggiore?

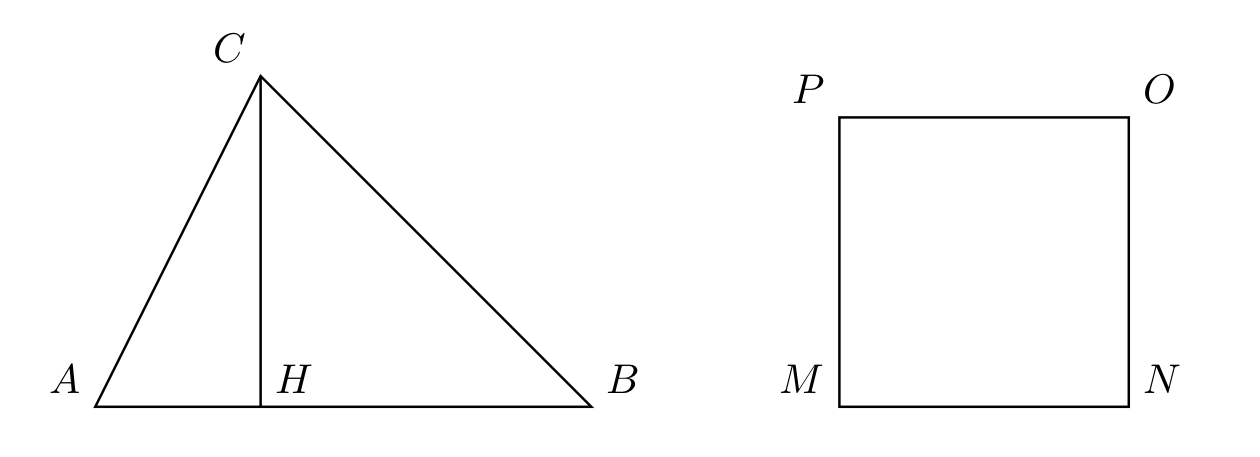
Può essere utile ricordare la seguente formula:
Disuguaglianza fra media aritmetica e media geometrica
Siano \(x_{1},x_{2}, \dots x_{n}\) numeri reali non negativi. Allora:

\[ \dfrac {x_{1}+ x_{2} + \cdots x_{n}}{n} \ge \sqrt[n]{x_{1}x_{2} \cdots x_{n}} \]

---

Esercizio 2

Fissata una sfera di raggio R, determinare l’altezza del cono inscritto di volume massimo.

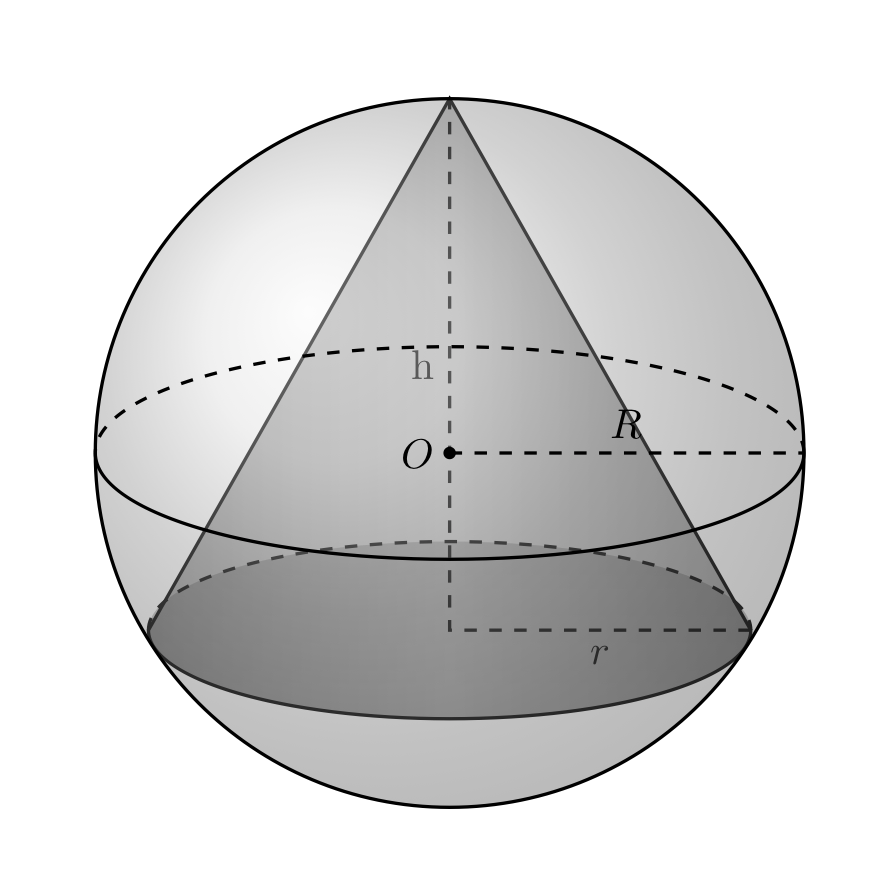
Risolvere anche senza utilizzare i metodi dell’analisi matematica (criterio delle derivata prima).

---

Esercizio 3

Sia \(T\) l’insieme di tutti i triangoli \(\triangle ABC\) che hanno un fissato angolo \(\alpha\) nel vertice \(A\) e una fissata area \(S\). Dimostrare che quello che ha la base \(BC\) più corta è un triangolo isoscele.

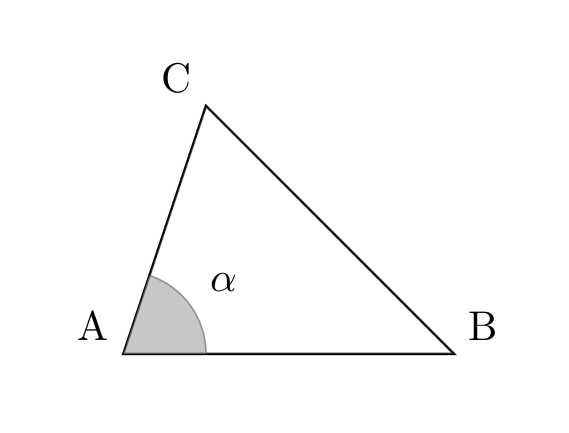
Risolvere anche senza utilizzare i metodi dell’analisi matematica (criterio delle derivata prima). Può essere utile ricordare le seguenti formule:

Teorema di Carnot (legge del coseno)
In un triangolo di lati \(a,b,c\) vale la seguente formula:

\[ a^2 = b^2 + c^2 – 2bc \cos \alpha \]

dove \(\alpha\) è l’angolo opposto al lato \(a\). Formule simili valgono per gli altri due lati \(b,c\).

Area di un triangolo
L’area di un triangolo di lati \(a,b,c\) vale:

\[ S = \frac{bc \sin \alpha}{2} \]

dove \(\alpha\) è l’angolo opposto al lato \(a\). Formule simili valgono per le altre due coppie di lati.