La geometria euclidea studia gli oggetti geometrici come le rette, i triangoli, i rettangoli, i cerchi, ecc. Anche i frattali sono oggetti geometrici; tuttavia hanno proprietà specifiche che li distinguono, e non possono essere classificati come oggetti della geometria classica. Nonostante Mandelbrot (1924-2010) venga considerato in generale il padre della teoria scientifica dei frattali, in realtà le idee che stanno alla base della teoria sono presenti in diversi studi matematici fin dai secoli precedenti.
Un esempio di oggetti geometrici che non rientrano nei modelli dell’analisi matematica classica sono le curve che riempiono tutto il piano, inizialmente studiate da Giuseppe Peano(1858-1932). Tra queste illustriamo la curva di Hilbert (1862-1943), cioè una curva frattale continua che riempie tutto il piano.
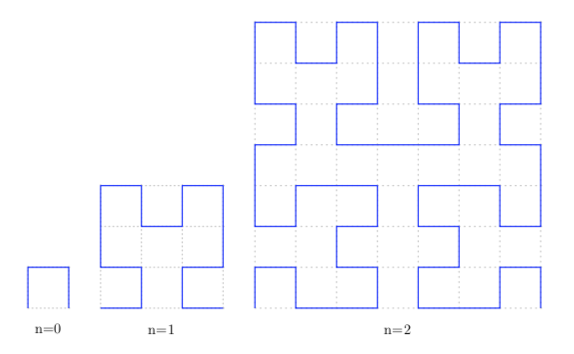

1) Proprietà dei frattali
Il concetto di frattale è spesso associato ad alcune proprietà che li distinguono dagli usuali oggetti geometrici. Tra queste proprietà ci sono le seguenti:
- autosimilarità
- irregolarità geometrica
- dimensione frazionaria
1.1) Autosimilarità
L’autosimilarità significa che l’oggetto è costituito da componenti che hanno una struttura simile all’oggetto intero. Gli oggetti autosimili scalano della stessa quantità in ogni direzione. Questa proprietà di struttura fine nei modelli matematici dei frattali vale ad ogni scala, mentre nel mondo reale ha chiaramente dei limiti (dovuti se non altro alla struttura molecolare e atomica).
Una generalizzazione dell’autosimilarità è l‘autoaffinità, cioè gli oggetti a scale diverse pur essendo approssimativamente autosimili, tuttavia possono essere diversi in base alla direzione, con effetti di dilatazione o contrazione.
Oltre agli oggetti astratti creati dalla matematica, esempi di frattali si trovano in natura. Le nubi, le montagne, le coste, i fiori, i cristalli di ghiaccio, ecc. sono tutti esempi di oggetti irregolari che difficilmente possono essere descritti con la geometria classica, e hanno proprietà approssimate di autosimilarità.
1.2) Irregolarità geometrica
Diversamente dalle curve e superfici dell’analisi classica, gli oggetti frattali presentano delle irregolarità ai vari livelli di scala. Ad esempio molte curve frattali, pur essendo continue, non ammettono la tangente in nessun punto, e quindi non è possibile applicare il concetto di derivata, così importante nell’analisi matematica classica.
1.3) Dimensione frazionaria
Gli oggetti della geometria classica hanno sempre dimensioni intere: \(0\) per il punto, \(1\) per le figure lineari (rette, curve, ecc), \(2\) per le figure piane (quadrato, cerchio, ecc), \(3\) per gli oggetti dello spazio (cubi, sfere, ecc). Nel mondo dei frattali invece è necessario generalizzare il concetto di dimensione, introducendo la possibilità di valori frazionari.
Per iniziare lo studio dei frattali, è necessario rivedere alcuni concetti della teoria degli insiemi.
2) Richiami sulla teoria degli insiemi
Un insieme è una collezione di oggetti distinti, chiamati elementi dell’insieme. Gli oggetti possono essere di natura qualsiasi: numeri, veicoli, persone, ecc. Un insieme può essere definito descrivendo il suo contenuto, oppure elencando gli elementi che appartengono all’insieme stesso. L’insieme universale è l’insieme che contiene tutti gli elementi del contesto di interesse. L’insieme vuoto non contiene alcun elemento. Il complemento di un insieme A è l’insieme \(A^{c}\) che contiene tutti gli elementi dell’universo che non appartengono ad A. Dati due insiemi A,B sono definite le operazioni di unione e intersezione:
\[ \begin{split} A \cup B = \{x: x \in A \quad oppure \quad x \in B \} \\ A \cap B = \{x: x \in A \quad e \quad x \in B \} \end{split} \]Definizione 2.1
Due insiemi A,B si dicono equipotenti (oppure hanno la stessa cardinalità) se esiste una corrispondenza biunivoca fra essi; cioè se esiste una funzione biiettiva \(f: A \to B\).
Ovviamente due insiemi finiti sono equipotenti se e solo se contengono lo stesso numero di elementi. La nozione di cardinalità di un insieme è stata sviluppata dal matematico Georg Cantor (1845-1918). La cardinalità di un insieme finito è data dal numero di elementi dell’insieme. Tuttavia per gli insiemi infiniti la situazione è più complessa.
Definizione 2.2
Un insieme infinito si dice numerabile se ha la stessa cardinalità dell’insieme dei numeri naturali \(\mathbb{N}\). Altrimenti si dice non numerabile.
Esercizio 2.1
Dimostrare che tutti i seguenti insiemi sono numerabili, trovando per ognuno una funzione biiettiva con l’insieme dei numeri naturali \(\mathbb{N}\):
- A – numeri interi positivi pari \( \{2,4,6, \cdots \}\)
- B – numeri interi positivi dispari \( \{1,3,5, \cdots \}\)
- \(\mathbb{N}\) – insieme dei numeri naturali \(\{1,2, \cdots \}\)
- \(\mathbb{Z}\) – insieme degli interi \(\{\cdots ,-3,-2,-1,0,1,2,3, \cdots \}\)
Si può dimostrare che anche l’insieme dei numeri razionali è numerabile. La scoperta fondamentale di Cantor è che invece l’insieme dei numeri reali (che comprende i razionali e gli irrazionali) non è numerabile. Si dice che l’insieme dei numeri reali ha la potenza del continuo.
Teorema 2.1
L’insieme dei numeri reali non è numerabile.
Dimostrazione
In realtà è sufficiente dimostrare che l’insieme dei numeri reali contenuti nell’intervallo \([0,1]\) è non numerabile. Il procedimento diagonale di Cantor utilizza il metodo di dimostrazione per assurdo. Supponiamo che sia possibile stabilire una corrispondenza biunivoca fra l’insieme dei naturali e l’intervallo \([0,1]\), cioè esista una funzione biiettiva \(f: \mathbb{N} \to [0,1]\). Elenchiamo questa corrispondenza mediante l’espansione binaria dei numeri reali compresi nell’intervallo \([0,1]\):
dove gli \(a_{ij}\) assumono i valori \(\{0,1\}\). Il procedimento diagonale di Cantor consiste nel determinare un numero reale compreso nell’intervallo che è diverso da tutti i numeri \(f(i)\). Il numero cercato ha la seguente espansione binaria: \(x=0.b_{1}b_{2}b_{3} \cdots\), dove le cifre \(b_{i}\) sono così definite:
\[ \begin{cases} b_{k}= 0 \quad se \quad a_{kk}=1 \\ b_{k}= 1 \quad se \quad a_{kk}=0 \end{cases} \]È evidente che per nessun valore di n si ha \(f(n)=x\) e quindi la funzione \(f\) non è biiettiva, contrariamente all’ipotesi.
Esercizio 2.2
Dimostrare che l’intervallo \((0,1)\) e la retta infinita \((-\infty,+\infty)\) hanno la stessa cardinalità.
Suggerimento: utilizzare una delle funzioni trigonometriche per trovare una una corrispondenza biunivoca fra i due insiemi.
Concludiamo qui questi richiami alla teoria degli insiemi. Per un ripasso della teoria elementare degli insiemi, con numerosi esercizi svolti, vedere ad esempio [1].
3) L’insieme di Cantor
L’insieme di Cantor è un altro esempio famoso di insiemi che non rientrano nei modelli della geometria euclidea e dell’analisi matematica classica. La costruzione dell’insieme di Cantor si basa su un processo iterativo semplice. Si prende un segmento unitario \([0,1]\) e si toglie il segmento centrale \((\frac{1}{3},\frac{2}{3})\), lasciando i punti estremi. Quindi si ripete la stessa procedura su ognuno dei due segmenti rimasti, e così via all’infinito.
L’insieme di Cantor consiste in tutti i punti dell’intervallo [0, 1] che non vengono eliminati in questo processo infinito di rimozione.

Una prima cosa interessante è calcolare la lunghezza complessiva dei segmenti eliminati:
\[ L=\frac{1}{3} + 2 \frac{1}{3^{2}} + 2^{2} \frac{1}{3^{3}}+ \cdots = \frac{1}{3} \sum_{k=0}^{\infty} \frac{2^{k}}{3^{k}}=1 \]in quanto si tratta di una serie geometrica (ricordiamo che per una serie geometrica \(\sum_{k=0}^\infty x^{k}= \frac{1}{1-x} \quad se \quad |x| <1\)).
A prima vista sembrerebbe quindi che il processo di taglio elimina tutti i punti e non rimane nulla del segmento iniziale. Tuttavia non è così; infatti avendo conservato i punti estremi dei segmenti questi non vengono mai eliminati; ad esempio il punto \(\frac{2}{3}\) della prima iterazione viene lasciato, e non ci sarà più nessun segmento che lo contiene al suo interno. Per comprendere esattamente quali e quanti punti dell’intervallo \([0,1]\) rimangono alla fine del processo iterativo, conviene esprimere i numeri reali dell’intervallo con il sistema ternario.
3.1) Il sistema ternario
Il sistema decimale utilizza i simboli \(\{0,1, \cdots 9\}\); il numero \(25_{10}\) in base \(10\) equivale a \(2 \cdot 10^{1}+ 5 \cdot 10 ^{0}\).
Il sistema ternario utilizza i simboli \(\{0,1,2 \}\) per esprimere lo sviluppo di un numero reale. Il numero \(221_{3}\) in base \(3\), equivale a \( 2 \cdot 3^{2} + 2 \cdot 3^{1}+ 1 \cdot 3^{0}=25_{10}\) . Il numero frazionario \(21,011_{3}\) equivale a \( 2 \cdot 3^{1} + 2 \cdot 3^{0}+ 0 \cdot 3^{-1} + 1 \cdot 3^{-2} + 1 \cdot 3^{-3}\) .
La rappresentazione dei numeri con il sistema ternario ci aiuta a comprendere cosa avviene nel processo iterativo di cancellazione di segmenti dell’insieme di Cantor sopra descritto. Nella prima iterazione viene rimosso l’intervallo centrale \((\frac{1}{3},\frac{2}{3})\). Di fatto vengono rimossi i numeri che nella base \(3\) hanno la cifra \(1\) nella posizione iniziale, esclusi gli estremi. Nella seconda iterazione viene rimosso l’intervallo centrale in ognuno dei due segmenti \([0,\frac{1}{3}]\) e \([\frac{2}{3},1]\). Di fatto in ognuno dei due intervalli vengono rimossi i numeri che hanno la cifra \(1\) nella seconda posizione dello sviluppo ternario. Proseguendo all’infinito possiamo concludere che nell’insieme di Cantor restano tutti i numero reali la cui espansione ternaria contiene solo le cifre \(0\) e \(2\). Quindi l’insieme di Cantor non è vuoto, come poteva sembrare a prima vista, ma contiene infiniti punti. Anzi si può dimostrare il seguente teorema:
Teorema 3.1
L’insieme di Cantor non è numerabile, ma ha la stessa potenza dell’insieme di tutti i numeri reali (potenza del continuo).
Per una dimostrazione vedere il testo citato in precedenza.
4) La dimensione degli oggetti frattali
Gli oggetti frattali, pur potendo essere rappresentati in uno spazio geometrico a 1,2,3 dimensioni, non hanno una dimensione intera. La dimensione di un oggetto frattale da una misura di quanto complicata è una figura autosimilare, di quanti punti giacciono in un dato insieme.
Ci sono differenti definizioni di dimensione; in questo articolo descriveremo la procedura box-counting, che è la più semplice e intuitiva, ed è comunque sufficiente per studiare gran parte degli oggetti frattali.
Per comprendere la motivazione che sta alla base della procedura box-counting prendiamo ad esempio un quadrato, che ha dimensione uguale a 2; dividendo il lati a metà otteniamo \(2^{2}=4\) quadrati di lati uguali ad \(\frac{1}{2}\) di quelli originali; se dividiamo il quadrato iniziale in quadrati di lato \(\frac{1}{3}\) otteniamo \(3^{2}=9\) quadratini di lati uguali ad \(\frac{1}{3}\) di quelli iniziali. Proseguendo possiamo dedurre una relazione importante fra il numero di quadratini prodotti \(N\), il fattore di scala \(f\) e la dimensione degli oggetti \(D\). La relazione è la seguente:
Calcolando il logaritmo naturale otteniamo le seguenti relazioni:
\[ \begin{split} \ln N = D \ln \frac{1}{f}= – D \ln f \\ D= -\frac{\ln N}{\ln f} \end{split} \]Definizione 4.1 – Dimensione Box-Counting
Diamo la definizione di dimensione di un oggetto frattale limitato contenuto nello spazio euclideo \(R^{3}\). Indichiamo con \(N(S,d)\) il numero di piccoli cubi di lato \(d\) necessari per ricoprire l’oggetto S. Ogni oggetto \(N(S,d)\) contiene quindi almeno un punto di S. L’idea è di prendere cubi con lato sempre più piccolo e definire la dimensione di S, come il limite della seguente espressione:
Nel caso di oggetti piani al posto dei cubi si utilizzeranno dei quadrati. Per gli oggetti contenuti su una retta si utilizzano dei segmenti. Naturalmente questa definizione ha senso solo se il limite esiste. In matematica esistono definizioni più avanzate, come la dimensione di Hausdorff-Besicovitch, che tuttavia non danno risultati diversi dalla box-counting nei casi più comuni. Per uno studio più avanzato si può consultare il testo [2].
Per gli oggetti della geometria euclidea, la definizione sopra proposta da gli stessi valori.
Esempio 4.1 – Dimensione del quadrato
Dato un quadrato Q di lato unitario. In questo caso, posto \(d=\frac{1}{n}\), abbiamo \(N(Q,\frac{1}{n})= \frac{1}{n^{2}}\). Applicando la formula troviamo:
Con lo stesso ragionamento si trova che il cubo ha dimensione 3.
Esempio 4.2 – Dimensione dell’insieme di Cantor
In base al processo di iterazione, possiamo calcolare il numero di componenti per ogni valore di n:
Quindi, applicando la definizione, abbiamo:
\[ \text {dim(S)} = \lim\limits_{n \to \infty} \frac {\ln(2^{n})}{\ln(3^{n})}=\frac {\ln(2)}{\ln (3)}= \approx 0.631 \]5) La curva di Koch e il fiocco di neve
Il fiocco di neve di Von Koch (1870-1924) è una curva costruita operando sui sui lati di un triangolo equilatero. Su ciascuno dei lati del triangolo viene costruita la curva di Koch (chiamata anche il merletto di Koch): si prende il lato, lo si taglia in 3 parti e si sostituisce quella centrale con due segmenti uguali a quello eliminato; si ripete l’operazione con ciascuno dei quattro segmenti così ottenuti e si continua per un numero infinito di volte. La figura che si ottiene, operando sui tre lati, dopo un numero infinito di iterazioni è il fiocco di neve di Koch. l merletto di Von Koch è chiaramente autosimilare, mentre il fiocco di neve non è strettamente autosimilare. Infatti ingrandendo uno dei lati dopo la prima iterazione otteniamo una copia del merletto e non del fiocco.
Si può dimostrare che la curva di Koch è continua in ogni punto, ma non è derivabile in alcun punto. L’immagine seguente illustra le prime 3 iterazioni del processo di suddivisione di un lato del triangolo.
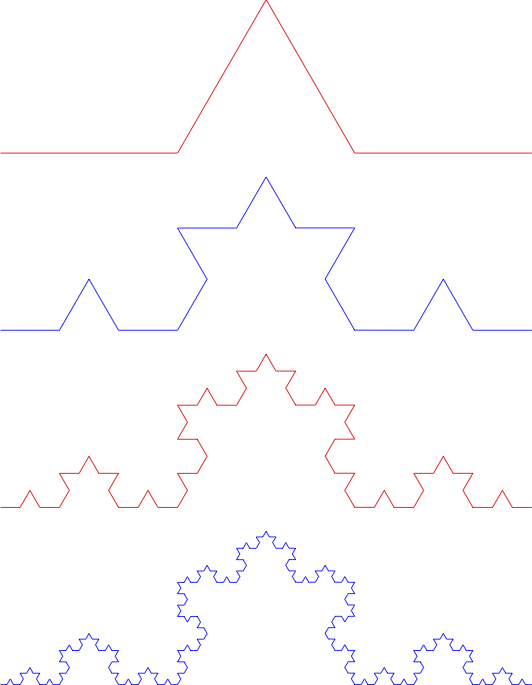
5.1) Lunghezza della curva di Koch e del fiocco di neve
Ad ogni iterazione la lunghezza della curva di Koch cresce di un fattore 4/3: se il segmento di partenza ha lunghezza pari a 1, il secondo misura 4/3, il terzo 16/9, il quarto 64/27 e così via. Quindi allo stadio \(n\) della costruzione abbiamo \(4^{n}\) segmenti, ognuno di lunghezza \(\frac{1}{3^{n}}\). La lunghezza totale \((\frac{4}{3})^{n}\) tende ad un valore infinito. Quindi possiamo concludere che il perimetro della curva di Koch e di conseguenza anche del fiocco ha valore infinito, pur essendo le due curve contenute in una regione limitata.
5.2) Dimensione della curva di Koch
Ad ogni passo dell’iterazione, ogni segmento della curva di Koch viene sostituito da 4 piccoli segmenti, ognuno di lunghezza uguale a \(\frac{1}{3}\) di quello iniziale. Quindi applicando la definizione di dimensione frattale, abbiamo:
\[ \text {dim(K)} = \lim\limits_{n \to \infty} \frac {\ln(4^{n})}{\ln(3^{n})}=\frac {\ln(4)}{\ln (3)}= \approx 1.262 \]5.3) Area del fiocco di neve di Koch
Supponiamo che il triangolo equilatero abbia lati unitari. L’area è quindi \(\frac{\sqrt{3}}{4}\). La prima iterazione aggiunge 3 triangoli. Ognuna delle successive aggiunge un numero di triangoli 4 volte quello precedente. Quindi alla iterazione n-esima vengono aggiunti \(3 \cdot 4^{n-1}\) triangoli. Possiamo scrivere la seguente equazione di ricorsione per l’area della figura: \(A_{n}= A_{n-1}+ \frac {3 \cdot 4^{n-1}}{9^{n}} A_{0}\), dove \(A_{0}\) è l’area del triangolo iniziale.
Si tratta di una equazione di ricorrenza che può essere risolta con i medodi delle equazioni alle differenze finite (per i quali si rimanda al testo [3]). Tuttavia in questo caso l’equazione è abbastanza semplice e con pochi passaggi elementari possiamo calcolare l’area \(A\) del fiocco di Koch:
dove abbiamo utilizzato la somma della serie geometrica.

6) Frattali e sistemi caotici
Lo sviluppo scientifico e tecnologico che caratterizza l’età moderna è basato sull’applicazione della matematica nelle varie discipline. Gli strumenti matematici hanno permesso negli ultimi secoli di prevedere e calcolare l’evoluzione dei fenomeni fisici con grande precisione, soprattutto nel caso che questi siano determinati da leggi lineari. Tuttavia, nonostante la disponibilità di computers sempre più potenti, molti fenomeni fisici rimangono fuori dalla possibilità di una previsione attendibile.
Il problema è che molti fenomeni fisici, economici e sociali hanno una natura caotica e non lineare, che impedisce di effettuare una previsione del comportamento futuro, in maniera attendibile. Numerosi sistemi naturali o artificiali come le economie, i mercati azionari, le reazioni chimiche, ecc. mostrano una grande dipendenza dalle condizioni iniziali. Anche piccole differenze nelle condizioni iniziali possono comportare grandi difference nell’evoluzione futura. Di fatto inoltre non si conoscono mai le condizioni iniziali con precisione assoluta e inoltre i modelli matematici e fisici sono sempre delle approssimazioni dei fenomeni reali. In questa situazione è pressoché impossibile ogni attendibile previsione futura a lungo termine.
I frattali sono spesso utilizzati per modellizzare i processi caotici, che nonostante abbiano un comportamento apparentemente casuale, presentano in dettaglio delle caratteristiche di autosimilarità. La scienza dei frattali non consiste quindi soltanto in complesse immagini grafiche generate mediante i computers, ma fornisce degli strumenti che permettono di creare dei modelli dei fenomeni complessi, con precisione in alcuni casi maggiore dei modelli tradizionali della matematica e della fisica.
Conclusione
La scienza dei frattali e dei sistemi caotici integra diverse discipline, come la matematica, la fisica, la computer graphics. È una vera e propria rivoluzione scientifica che permetterà di fare importanti progressi nella ricerca di modelli sempre più precisi per studiare sia gli oggetti matematici complessi sia l’evoluzione dei fenomeni del mondo reale.
Per un approfondimento dello studio dei frattali si possono consultare i seguenti libri [4] e [5].
Bibliografia
[1]Lipschutz – Set Theory and Related Topics (McGraw-Hill)
[2]M. Barnsley – Fractals EveryWhere (Dover Books)
[3]M. Spiegel – Differenze finite e equazioni alle differenze (Etas Libri)
[4]Mandelbrot – The Fractal Geometry of Nature – Set Theory and Related Topics (Times Books)
[5]Falconer – Fractal Geometry (Wiley)
0 commenti