In questo articolo vengono descritte le forme geometriche primitive utilizzate nelle collisioni 2D, con riferimenti alle funzionalità messe a disposizione dal motore fisico Unity Physics 2D. Per un ripasso dell’algebra vettoriale, necessaria per comprendere l’argomento, si può vedere anche l’articolo pubblicato su questo sito.
La gestione delle collisioni fra due o più oggetti può essere suddivisa in due fasi principali:
- rilevazione delle collisioni (collision detection)
- azioni di risposta alle collisioni (collision response)
In molti videogiochi è fondamentale riuscire a gestire il problema del rilevamento e risposta alle collisioni con il necessario livello di accuratezza ed efficienza. Il problema è più semplice se gli oggetti hanno forme geometriche regolari, mentre in presenza di oggetti di forma irregolare diventa estremamente complesso e può essere affrontato con metodi di approssimazione.
I moderni framework per lo sviluppo dei giochi, come Unity o Unreal Engine, forniscono strumenti software sofisticati che permettono allo sviluppatore di gestire il problema in modo intuitivo, senza entrare nel dettaglio degli algoritmi matematici e delle leggi fisiche. Tuttavia un certo livello di conoscenza delle modalità di funzionamento del motore fisico è indispensabile anche per un programmatore applicativo.
Nel seguito, per definire strutture dati e schemi di algoritmi viene utilizzato uno pseudocodice che di massima utilizza la sintassi del linguaggio C.
1) Forme geometriche primitive 2D
Per prevedere e analizzare la collisione fra due oggetti, è necessario in primo luogo definire le forme geometriche di base che questi possono assumere. Ad esempio:
– il punto
– la retta o il segmento
– il cerchio
– il rettangolo
1.1) Il punto e il vettore 2D
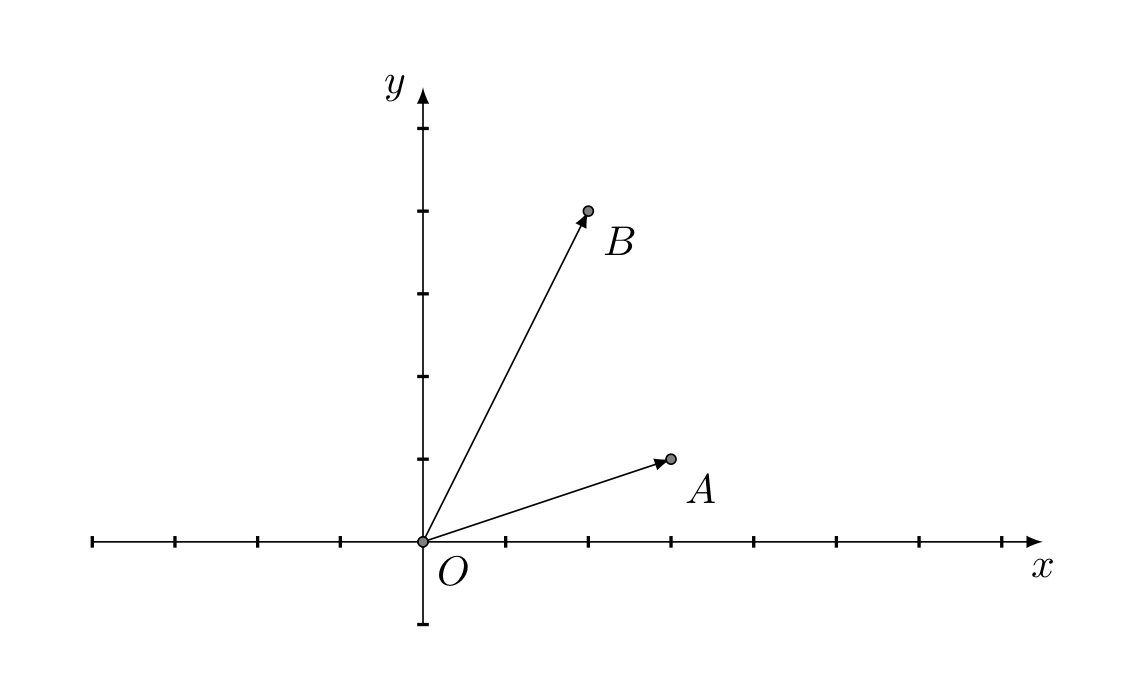
È la forma primitiva più semplice. Un punto è definito dalle sue coordinate cartesiane x,y. Ad ogni punto 2D corrisponde un vettore applicato nell’origine del sistema di coordinate. Quindi possiamo parlare in modo equivalente sia di punti che di vettori.
// definizione della struttura
typedef struct {
float x;
float y;
} Vector2D;
// Creazione di un oggetto del tipo Vector2D
Vector2D vettore = (5,3.5); La distanza fra due punti può essere determinata calcolando il modulo (o intensità) del vettore che risulta dalla differenza dei due vettori.
1.2) La retta e il segmento
La retta può essere definita conoscendo un punto e la direzione, oppure conoscendo due punti che appartengono alla stessa. La definizione della struttura della retta secondo il primo punto di vista è la seguente:
// definizione della struttura
typedef struct {
Vector2D punto_base;
Vector2D direzione;
} Retta;
// Creazione di un oggetto del tipo Retta
Vector2D p_base = (1,0);
Vector2D direzione = (1,1);
Retta r1 = {p_base,direzione}; Un segmento è la parte di retta compresa fra due punti. La struttura del segmento è la seguente:
// definizione della struttura
typedef struct {
Vector2D punto_inizio;
Vector2D punto_fine;
} Segmento;
// Creazione di un oggetto del tipo Segmento
Vector2D p_inizio = (1,2);
Vector2D p_fine = (5,4);
Segmento s1 = {p_inizio,p_fine};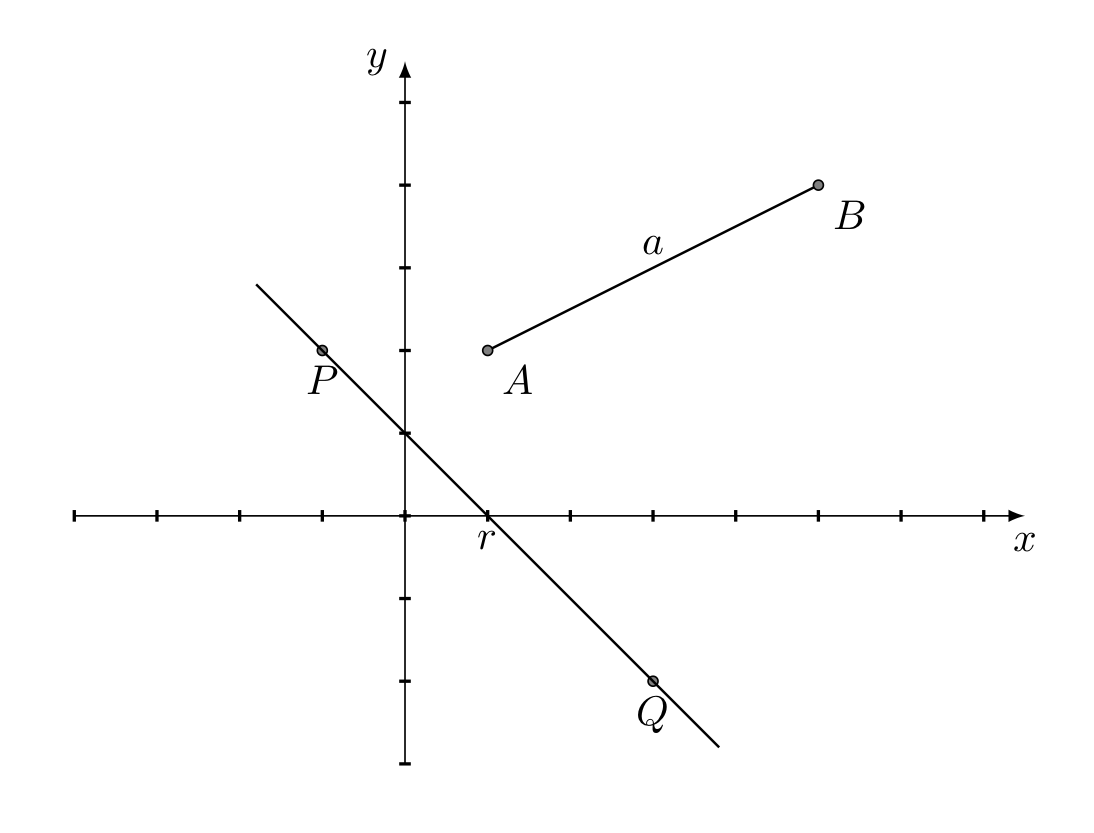
1.3) Il cerchio
Il cerchio è definito specificando un punto, detto il centro, e il raggio. È una delle figure più utilizzate per approssimare le superfici dei vari oggetti. La definizione della struttura del cerchio è la seguente:
// definizione della struttura
typedef struct {
Vector2D centro;
float raggio;
} Cerchio;
// Creazione di un oggetto del tipo Cerchio
Vector2D p_centro = (3,3);
float r = 2.0;
Cerchio cerchio = (p_centro,r); 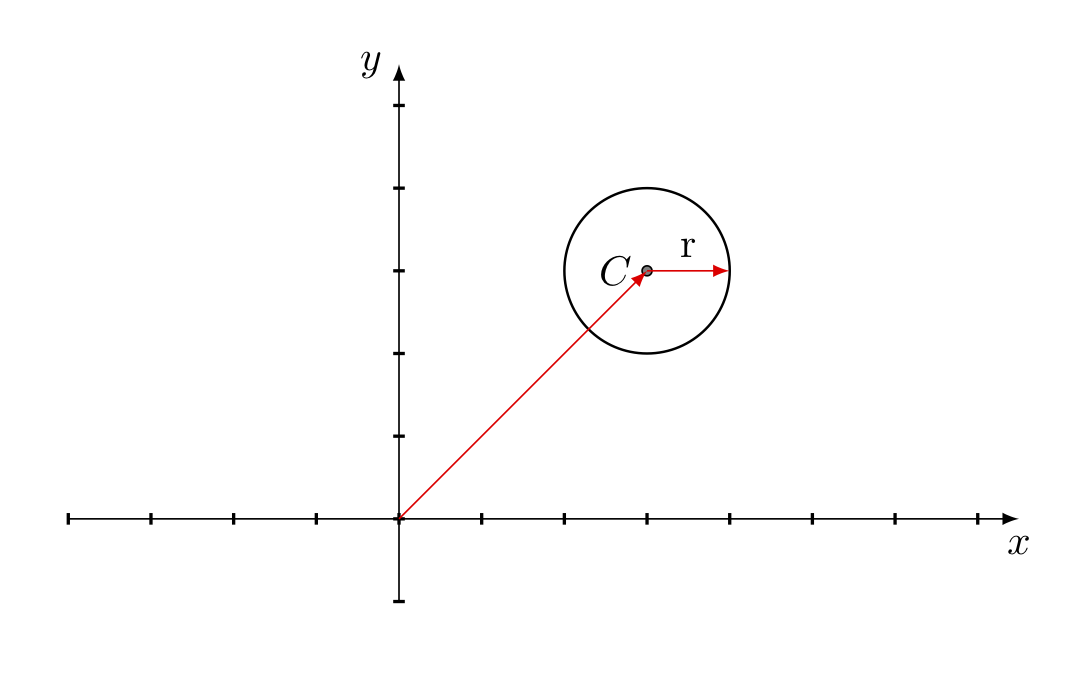
1.4) Il rettangolo
Un rettangolo ha 4 lati con angoli di 90 gradi. Può essere rappresentato in diversi modi. Un modo semplice è quello di definire come origine uno dei 4 vertici e aggiungere le dimensioni della larghezza e dell’altezza (sostanzialmente il vettore diagonale definito con una struttura Vector2D). La definizione della struttura del rettangolo con lati paralleli agli assi coordinati è la seguente:
// definizione della struttura
typedef struct {
Vector2D punto_origine;
Vector2D dimensioni;
} Rettangolo;
// Creazione di un oggetto del tipo Rettangolo
Vector2D p_origine = (-3,2);
Vector2D d = (2,1);
Rettangolo rettangolo = (p_origine,d); Se il rettangolo non è allineato agli assi cartesiani bisogna aggiungere l’informazione sulla rotazione. Inoltre in questo caso è preferibile utilizzare il centro del rettangolo e la metà dei valori della larghezza e della lunghezza.
// definizione della struttura
typedef struct {
Vector2D punto_centrale;
Vector2D dimensioni_dimezzate;
float rotazione;
} RettangoloOrientato;
// Creazione di un oggetto del tipo RettangoloOrientato
Vector2D p_centro = (2.5,2.5);
Vector2D d_dime = (0.5,1.5);
float rot = 45;
RettangoloOrientato rett_or = (p_centro,d_dime,rot); 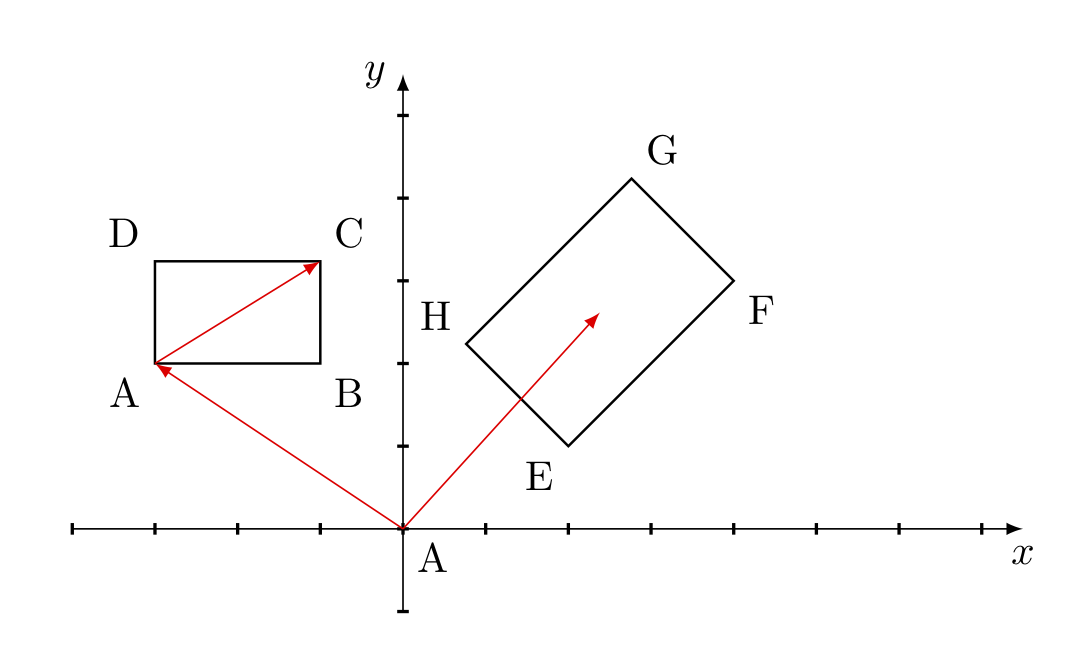
2) Rilevamento delle collisioni 2D
Un gioco può contenere in genere diversi oggetti, anche centinaia. Alcuni oggetti non sono interessati alle collisioni, altri possono avere solo singole collisioni, mentre altri possono avere collisioni multiple.
Un componente fondamentale del game engine è il sottosistema dedicato alla gestione delle collisioni. Uno degli scopi principali di questo sottosistema è il rilevamento delle collisioni, cioè la capacita di stabilire se due o più oggetti del gioco sono venuti in contatto. Ogni oggetto viene rappresentato con una o diverse forme geometriche. Il sistema deve quindi rilevare se le forme geometriche associate agli oggetti si sovrappongono in un certo istante di tempo. I complessi calcoli matematici e fisici che permettono di gestire le collisioni sono effettuati da software specializzati (come Box2D, PhysX) che forniscono il loro servizi ai framework applicativi, come Unity o Unreal Engine. Per effettuare i calcoli questi programmi hanno bisogno di due informazioni fondamentali: la forma e la posizione (transform). Una volta associato ad ogni oggetto una forma geometrica precisa, il rilevamento delle collisioni si riduce a calcolare l’intersezione delle forme, mediante gli strumenti della geometria analitica.
2.1) Collisione cerchio con punto
Il criterio è ovvio: un punto si trova dentro un cerchio se la distanza del punto dal centro del cerchio è minore del raggio. Conoscendo la posizione del punto, del centro e del raggio si trova subito la risposta.
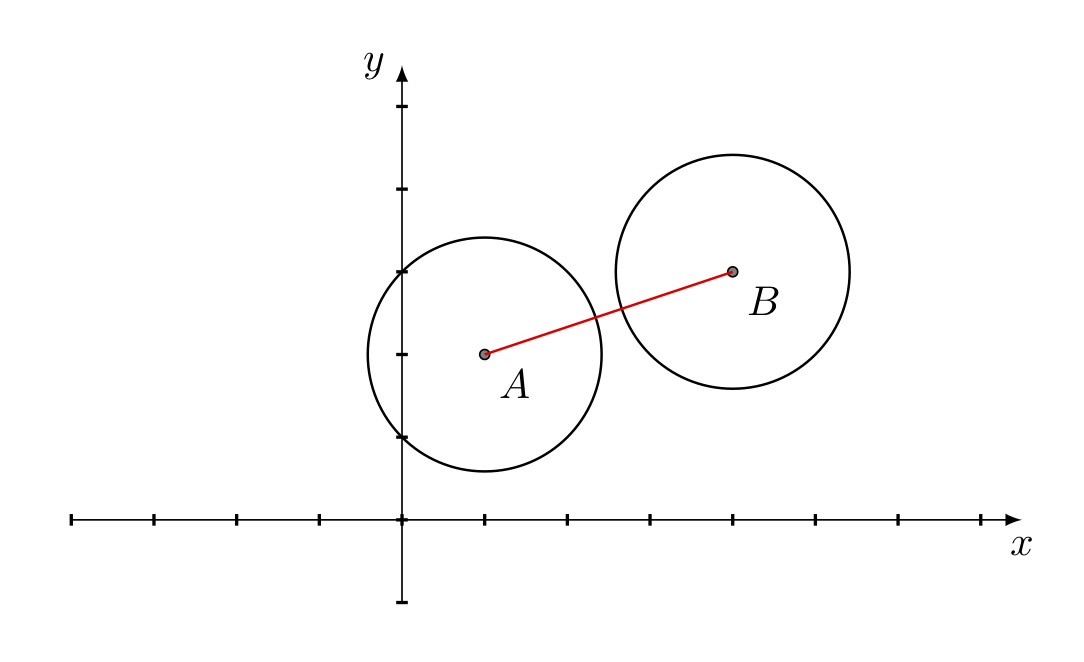
2.2) Collisione cerchio con cerchio
Il criterio è abbastanza semplice: due cerchi si intersecano se la distanza dei due centri è minore della somma dei due raggi. Conoscendo la posizione dei centri dei due cerchi e la lunghezza dei raggi, basta calcolare la lunghezza del segmento che congiunge i due centri e confrontare con la somma dei due raggi. Per motivi di efficienza è meglio confrontare direttamente i quadrati, evitando di effettuare l’operazione di radice quadrata.
2.3) Collisione cerchio con rettangolo
Questo problema viene semplificato trovando il punto sul rettangolo più vicino al centro del cerchio. Nel diagramma riportato sotto, il punto E è il più vicino.
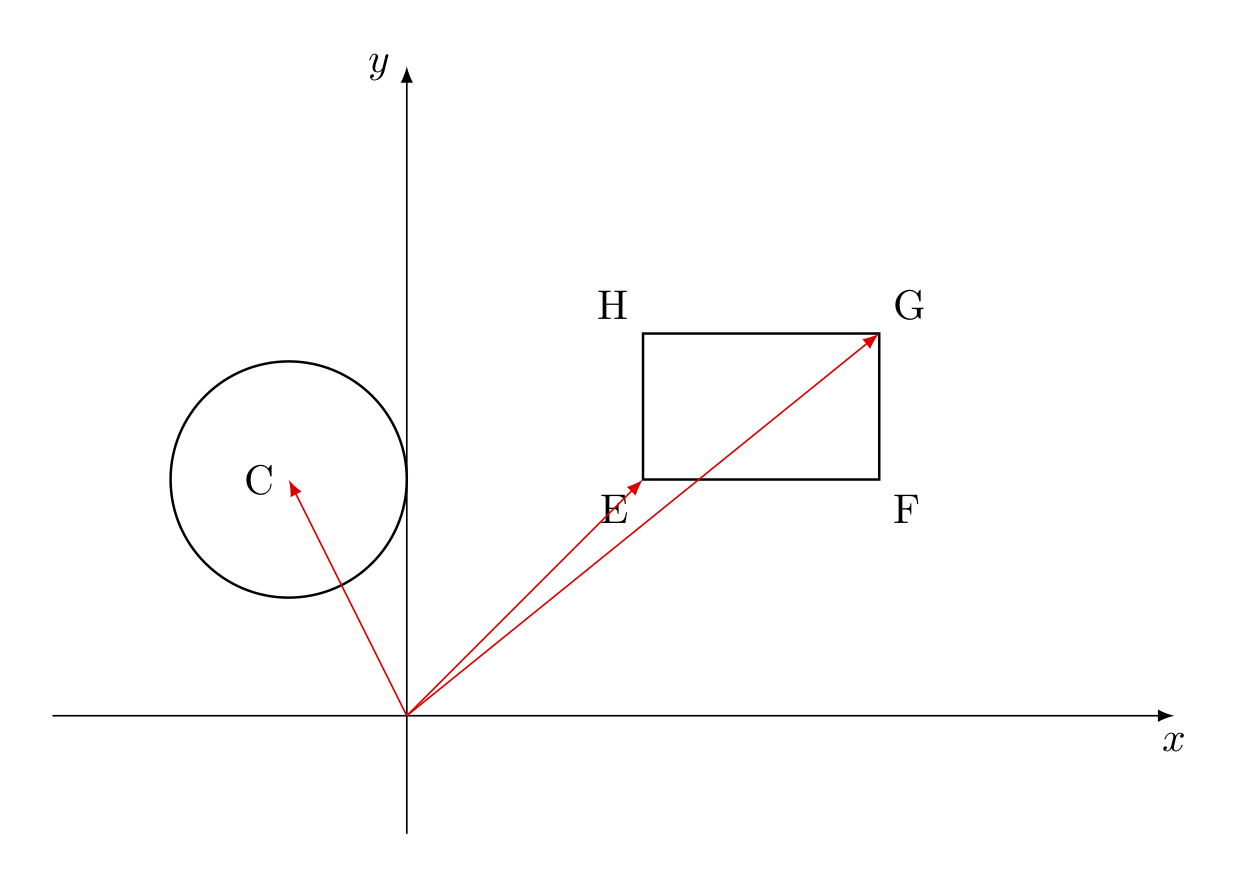
Uno schema di massima dell’algoritmo è il seguente:
bool CollCerchioRett(Cerchio cerchio, Rettangolo rect) {
// Trova il punto di minima ascissa e ordinata del rettangolo
Vector2D min = TrovaPuntoMinimo(rect);
// Trova il punto di massima ascissa e ordinata del rettangolo
Vector2D max = TrovaPuntoMassimo(rect);
// Trova il punto del rettangolo più vicino al centro del cerchio.
// Se il centro del cerchio è all'interno del rettangolo,
// allora il centro viene preso come punto più vicino e la
// distanza si assume uguale a zero.
Vector2D puntoVicino = cerchio.centro;
if (puntoVicino.x < min.x) {
puntoVicino.x = min.x;
}
else if (puntoVicino.x > max.x) {
puntoVicino.x = max.x;
}
if (puntoVicino.y < min.y) {
puntoVicino.y = min.y;
}
else if (puntoVicino.y > max.y) {
puntoVicino.y = max.y;
}
Segmento segmento = {cerchio.centro, puntoVicino};
// Confrontiamo i quadrati delle lunghezze per evitare le
// operazioni di radice quadrata
if (QuadratoLunghezza(segmento) < cerchio.raggio * cerchio.raggio)
return true;
else
return false;
} Se il rettangolo è in posizione obliqua rispetto agli assi coordinati, è necessario effettuare una trasformazione di coordinate per ridursi al caso precedente. Altri casi interessanti da analizzare sono i seguenti:
- collisione cerchio-retta o segmento
- collisione rettangolo-rettangolo
- collisione rettangolo-retta o segmento
- collisione punto-retta
2.4) Il teorema di separazione degli assi (SAT)
Per determinare se due figure geometriche arbitrarie si intersecano può essere utilizzato il teorema di separazione degli assi, il quale afferma che se esiste un asse lungo il quale le proiezioni di due figure geometriche non si sovrappongono, allora le due figure geometriche non hanno punti in comune.
In ambiente 2D il teorema è evidente: se un oggetto A giace completamente da una parte di una retta e un oggetto B dall’altra, allora i due oggetti A,B non si sovrappongono.
La retta viene chiamata retta di separazione e la perpendicolare è l’asse di separazione.
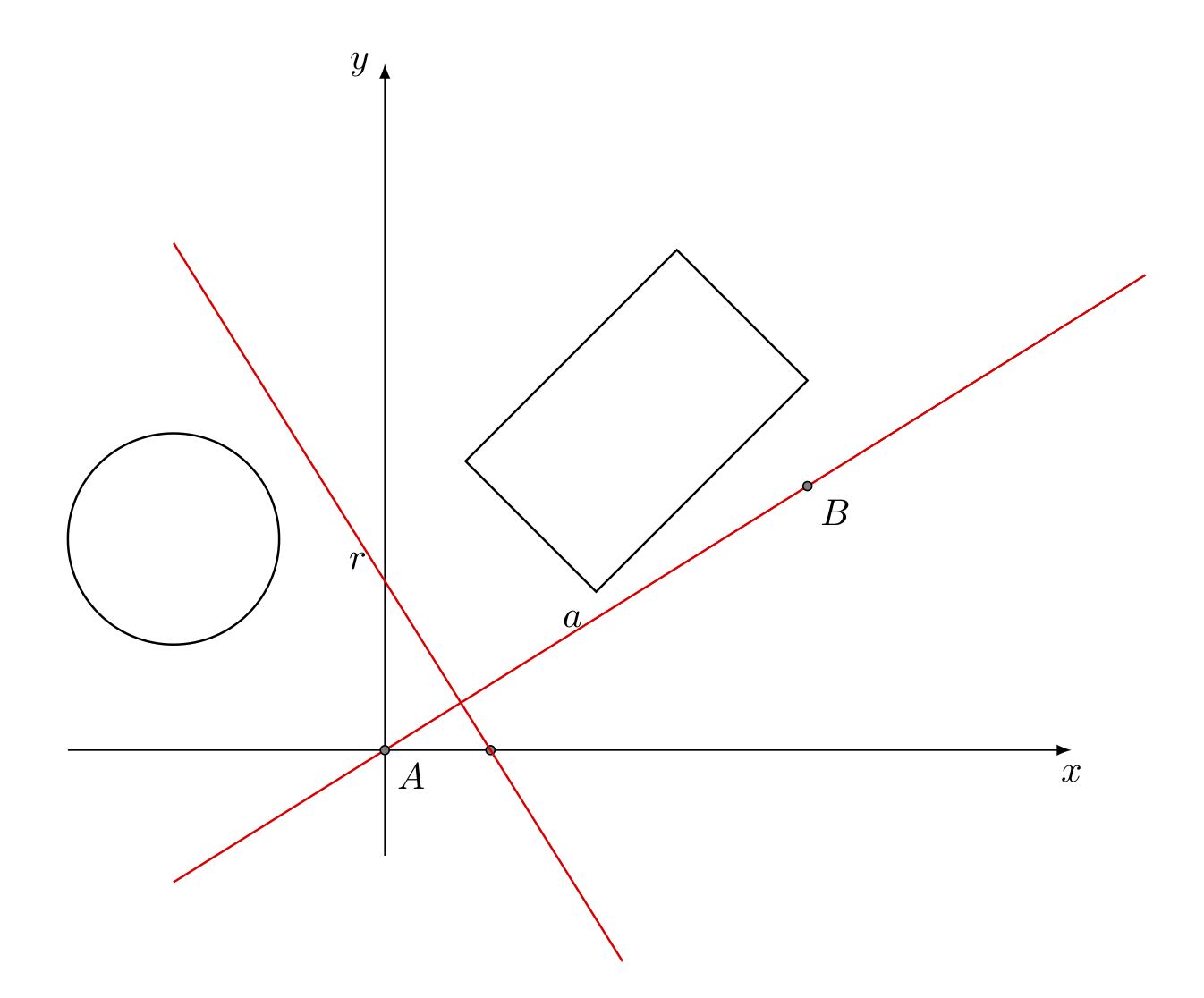
Nel diagramma la retta a è l’asse separatore e la retta r è la retta separatrice. Nello spazio 3D al posto della retta separatrice c’è il piano separatore. La struttura base per l’algoritmo SAT nel caso di due rettangoli con lati paralleli agli assi coordinati è la seguente:
SAT_Rett1Rett2(Rettangolo rett1, Rettangolo rett2) {
// scelta due assi di proiezione
Vector2D assi[] = {Vector2D(1, 0), Vector2D(0, 1)};
// ciclo per controllo sovrapposizione con i due assi
for (int i = 0; i < 2; i++) {
if (!VerificaSovrappAssi(rect1, rect2, assi[i]))
{
// Non c'è collisione
return false;
}
}
// C'è collisione
return true;
}La parte centrale dell’algoritmo SAT è lo sviluppo del metodo VerificaSovrappAssi; ad ogni chiamata per ognuno dei due rettangoli deve calcolare l’intervallo di proiezione sull’asse; quindi deve verificare se i due intervalli si sovrappongono. Per calcolare la proiezione si può utilizzare il prodotto scalare fra il singolo asse e i quattro vertici del rettangolo.
Nel caso di rettangoli orientati rispetto agli assi cartesiani l’algoritmo è leggermente più articolato.
3) Gestione collisioni complesse
La gestione delle collisioni dipende dalla forma geometrica e dal numero degli oggetti in gioco. Il problema è trattabile con relativa semplicità per le forme geometriche regolari (cerchi, rettangoli, segmenti, ecc.) e anche in questo caso solo se il numero degli oggetti non è elevato. Senza queste due condizioni la complessità del problema aumenta in modo esponenziale e diventa proibitiva, pur avendo a disposizione grande potenza di calcolo.
In tutti i campi della scienza, quando la complessità diventa elevata l’unica soluzione consiste nel ricorso ad algoritmi di approssimazione e ottimizzazione, che permettono spesso di raggiungere un soddisfacente livello di precisione. Alcuni tra i metodi di approssimazione usati sono i seguenti.
3.1) Il cerchio contenitore (bounding circle)
Data una figura geometrica regolare o non regolare, si cerca di incapsulare la figura con un cerchio di raggio minimo. La procedura richiede 3 passi:
1) approssimare la figura con un insieme finito di punti che seguono il contorno;
2) determinare il centro del cerchio a partire dall’insieme dei punti;
3) determinare il raggio del cerchio contenitore, che è la massima distanza dei punti dal centro.
Uno schema di massima dell’algoritmo C è il seguente:
Cerchio CerchioCont(Vettore2D[] listaPunti, int numPunti) {
Vettore2D centro;
float raggio;
// trova il centro del cerchio contenitore
centro = listaPunti[0];
for (int i = 1; i < numPunti; i++) {
centro = centro + listaPunti[i];
}
centro = centro / (float)numPunti;
// determina il quadrato del raggio del cerchio
raggio = LunghezzaQuad(centro - listaPunti[0]);
for (int i = 1; i < numPunti; ++i) {
float d = LunghezzaQuad(centro - listaPunti[i]);
if (d > raggio) {
raggio = d;
}
}
Cerchio cerchio(centro, sqrtf(raggio));
return cerchio;
} L’animazione successiva illustra la procedura nel caso del rettangolo contenuto in un cerchio.

3.2) Il rettangolo contenitore (bounding rectangle o box)
L’algoritmo è simile a quello del cerchio. Vengono analizzati i punti della figura e vengono determinati i punti di minimo e massimo con i quali costruire il rettangolo minimo che contiene tutti i punti della figura.
Il vantaggio del rettangolo è che rende più veloce la rilevazione delle collisioni. Il cerchio invece ha il vantaggio di non dipendere dalla rotazione, mentre il rettangolo necessita di effettuare un ricalcolo ogni volta che c’è una rotazione.
3.3) Strutture multiple
In alcune situazioni la figura non viene approssimata bene da un solo cerchio o un solo rettangolo. Invece è preferibile utilizzare diverse figure geometriche semplici per approssimare le varie parti della figura.
Per uno studio approfondito degli algoritmi di collisione vedere [1].
4) Il motore fisico Unity Physics 2D
I videogiochi cercano di simulare il mondo reale. Gli oggetti (GameObjetcs) che interagiscono nella scena sono identificati ognuno dalle coordinate cartesiane (x,y,z) nello spazio 3D, oppure dalle (x,y) in 2D. Per ogni oggetto è necessario applicare le leggi della fisica ed effettuare i calcoli necessari per determinare la velocità, l’accelerazione, la frequenza di rotazione, il risultato degli urti con altri oggetti, ecc.
Nelle versioni più recenti di Unity è stato aggiunto un componente specifico per la gestione della fisica degli oggetti sulla scena 2D, il motore fisico Physics 2D. Scopo del Physics 2D è di simulare le leggi della fisica, in particolare le leggi del movimento della meccanica classica basata sulle tre leggi di Newton. È bene ricordare che i motori fisici Unity 2D e 3D sono completamente separati. Il motore 3D utilizza il prodotto software PhysX, mentre il motore 2D utilizza Box2D.
I parametri del motore Physics 2D vengono impostati mediante il Physics 2D manager (Edit > Project Setting > Physics2D).
4.1) Il componente Rigidbody 2D
In Unity 2D è stato introdotto il componente Rigidbody2D, che deve essere associato ad ogni oggetto (ad esempio una sprite) che deve comportarsi come un corpo rigido, sottoposto a dei campi di forza come la gravità. Un oggetto cui è associato il componente Rigidbody2D viene messo sotto il controllo del motore fisico Physics 2D. Il componente Rigidbody2D definisce le proprietà fisiche quali l’intensità della gravità, la massa, l’attrito, ecc. Gli oggetti Rigidbody 2D possono muoversi solo nel piano XY e possono ruotare intorno all’asse Z. Unity da comunque la possibilità di annullare gli effetti della gravità per l’intera scena (Edit > Project Settings > Physics 2D), oppure per un singolo oggetto, aggiornando il componente Rigidbody2D.
4.2) Il componente collider 2D
In Unity 2D le collisioni non sono definite direttamente dal Rigidbody 2D, ma da nuovi componenti chiamati Collider 2D. Si tratta di componenti che definiscono una regione del piano nella quale può verificarsi l’interazione fra gli oggetti. Queste regioni in genere hanno una forma diversa dagli oggetti stessi, tranne nei casi di oggetti di forma geometrica semplice. I componenti Collider 3D hanno estensione in tutte e tre le dimensioni dello spazio, mentre i componenti Collider 2D collidono indipendentemente dalla posizione lungo l’asse z (è come se avessero estensione z infinita). I principali componenti Collider 2D sono i seguenti:
- Box Collider 2D – per forme quadrate o rettangolari
- Circle Collider 2D – per forme circolari
- Polygon Collider 2D – per le forme libere
- Edge Collider 2D – non richiedono che la forma sia chiusa
Il Polygon Collider 2D permette di creare collider più precisi; mediante l’Edit Collider è possibile modificare le forme geometriche muovendo, aggiungendo o cancellando vertici. Per l’elenco completo vedere il manuale online Unity.
Quando un oggetto deve simulare le leggi della fisica, come ad esempio un proiettile soggetto alla gravità, allora è necessario associare sia il Rigidbody2D sia il Collider2D. Nei casi nei quali si vuole rilevare soltanto la collisione fra due oggetti, allora il componente Rigidbody può essere trascurato, anche se comunque uno dei due deve avere attaccato il componente Rigidbody (Component>Physics 2D>Rigidbody 2D).
Ci sono tre tipi principali di Collider 2D e sono i seguenti.
4.2.1) Collider statici
Non hanno associato il componente Rigidbody e quindi non vengono gestiti dal motore fisico. Vengono utilizzati soprattutto per terreni, pareti fisse, ecc. Possono interagire con i collider dinamici, ma non si muovono in risposta a delle collisioni.
4.2.2) Collider dinamici
A essi è associato il componente Rigidbody e l’opzione booleana isKinematic dell’editor è impostata a falso. Il loro movimento viene gestito dal motore fisico in funzione delle forze e dei momenti di forza applicati su di essi. Il motore fisico gestisce anche le collisioni con altri collider statici, dinamici o cinematici.
4.2.3) Collider cinematici
Questi collider hanno associato il componente Rigidbody, tuttavia hanno impostata a vero l’opzione isKinematic nell’editor. Questo comporta che il movimento di questi oggetti non viene gestito dal motore fisico; in eventuali collisioni solo i collider dinamici rimbalzeranno. Gli oggetti con i collider cinematici non cambiano la loro velocità e direzione a meno che non vengano eseguite istruzioni applicative come MovePosition() oppure MoveRotation().
4.3) Matrici di collisione
Quando due oggetti collidono, vengono attivati diversi script per la gestione degli eventi. Gli eventi che vengono generati dipendono dalla configurazione scelta per gli oggetti nella scena. Gli oggetti, se non viene stabilito altrimenti, vengono creati sul livello (Layer) di Default dove ognuno può collidere con tutti gli altri. Tranne in casi semplici, è preferibile definire anche altri livelli (Edit > Project Settings > Tag and Layers) e assegnare i livelli ai vari oggetti tramite l’Inspector. Per ogni nuovo livello creato viene aggiunta una riga e una colonna nella matrice delle collisioni.
Nella matrice, tramite l’editor, possono essere impostate le regole di collisioni per i vari oggetti associati ai vari livelli.
4.4) Il materiale fisico 2D (Physics Material 2D)
Il materiale fisico 2D è un componente che può essere associato ad un GameObject, per definire le caratteristiche fisiche dell’oggetto stesso. Il materiale fisico contiene due proprietà: Bounciness (quanto l’oggetto rimbalza dopo un urto) e Friction (l’attrito). Una scelta corretta permette di simulare con maggiore precisione il comportamento di oggetti reali nei processi fisici, ad esempio nelle collisioni con altri oggetti.
5) Rilevazione collisioni in Unity 2D
Unity fornisce tre metodi principali (chiamati callbacks) per rilevare le collisioni relative ad un oggetto:
- OnCollisionEnter2D – chiamato quando un collider/rigidbody viene a contatto con un rigidbody/collider
- OnCollisionStay2D – chiamato fino a che il collider è dentro la zona di contatto
- OnCollisionExit2D – chiamato quando il collider esce dalla zona di contatto
I tre metodi vengono chiamati da Unity nel ciclo del motore fisico (fixed time step). Vengono attivati soltanto sull’oggetto che ha il componente Rigidbody2D.
using UnityEngine;
using System.Collections;
using UnityEngine.EventSystems;
using UnityEngine.UI;
public class BoxColliderScript : MonoBehaviour {
void Start () {
}
void OnCollisionEnter2D (Collision collisionInfo) {
Debug.Log("Inizio collisione");
}
void OnCollisionStay2D (Collision collisionInfo) {
Debug.Log("Collisione in corso");
}
void OnCollisionExit2D (Collision collisionInfo){
Debug.Log("Fine collisione");
}
}6) I trigger collider
I trigger sono un tipo speciale di collider. Per attivarli bisogna impostare l’opzione isTrigger nell’inspector del collider stesso. Con questa opzione il collider viene ignorato dal motore fisico. I trigger quindi non collidono fisicamente con altri oggetti, ma rilevano soltanto il passaggio di ogni altro collider all’interno della loro zona di potenziale collisione, permettendo all’applicazione di effettuare eventuali elaborazioni in funzione degli eventi. Unity registra gli eventi e chiama i seguenti metodi, che possono essere gestiti dall’applicazione nello script collegato all’oggetto che contiene il collider:
- OnTriggerEnter2D – quando il collider entra nella zona di un trigger
- OnTriggerStay2D – quando il collider rimane all’interno del trigger
- OnTriggerExit2D – quando il collider esce dal trigger
La seguente immagine mostra una palla con il circle collider 2D che si muove orizzontalmente fra tre pareti.

La palla ha anche associato il componente Rigidbody, con l’intensità della gravità (Gravity Scale) impostato a zero. Le pareti esterne hanno soltanto il collider 2D statico, mentre quella intermedia ha un trigger collider 2D. Quando la palla si avvicina alle pareti esterne avviene la collisione e vengono attivati gli eventi OnTrigger. Il motore fisico Unity applica le leggi della meccanica, in particolare il principio di conservazione della quantità di moto, in base al quale al momento dell’urto con le pareti destra e sinistra la palla inverte la direzione di 180 gradi, mantenendo sempre il moto orizzontale.
Quando la palla passa attraverso la parete intermedia, non avviene nessuna collisione, tuttavia vengono attivati gli eventi OnTrigger. Nel caso in esame in occasione dell’evento OnTriggerEnter2D tramite uno script associato all’oggetto palla viene impostato il colore rosso, mentre con l’evento OnTriggerExit2D viene impostato il colore blu.
Conclusione
La gestione delle collisioni è presente in gran parte dei videogiochi: collisioni fra caratteri, fra un oggetto e una parete o un pavimento, fra un proiettile ed un bersaglio, ecc. In molti videogame di successo, come Super Mario Bros, la gestione corretta del rilevamento e della risposta alle collisioni gioca un ruolo fondamentale. È essenziale che gli sviluppatori di videogiochi comprendano gli aspetti teorici e anche gli eventuali limiti dei motori fisici.
In questo articolo abbiamo discusso il caso delle collisioni nell’ambiente bidimensionale. In un prossimo articolo descriveremo la gestione delle collisioni 3D, sia nei loro aspetti matematici, sia nel contesto del motore fisico Unity 3D.
Bibliografia
[1]C. Ericson – Real-Time Collision Detection (Morgan Kaufmann)


0 commenti