In questo articolo viene fatta una breve illustrazione delle leggi della dinamica del moto nel piano e vengono analizzati gli strumenti che il motore Unity 2D mette a disposizione dei programmatori per simulare il movimento dei corpi nell’ambiente 2D.
Per lo studio della fisica è essenziale conoscere le unità di misura delle grandezze fondamentali e di quelle derivate, come definite nel Sistema Internazionale (SI). Le grandezze di base della meccanica sono riportate nella seguente tabella:

Per un ripasso esaustivo delle unità di misura vedere il seguente link.
1) Concetti di cinematica
La cinematica è la branca della meccanica che studia il moto dei corpi senza considerare l’azione delle forze in gioco. Le principali quantità fisiche oggetto di studio sono: posizione, velocità e accelerazione. Il caso più semplice da studiare è quello di un corpo puntiforme con dimensioni trascurabili per il contesto in cui si muove. Utilizzeremo la dizione standard di punto materiale: praticamente un punto geometrico che si muove nel piano secondo una certa traiettoria, cui può essere associata una massa \(m\).
1.1) Posizione
Per specificare la posizione di un oggetto bisogna scegliere un sistema di riferimento. Per un moto rettilineo basta un parametro per specificare la posizione di un oggetto. Nel piano abbiamo bisogno di due parametri, ad esempio le coordinate (x,y) di un sistema di assi cartesiani. Nello spazio abbiamo bisogno di tre parametri. È utile introdurre l’utilizzo dei vettori; la posizione di un oggetto che si trova in un punto \(P\) del piano, rispetto all’origine \(O\), può essere definita tramite il vettore posizione \( \mathbf{r}(t)\):
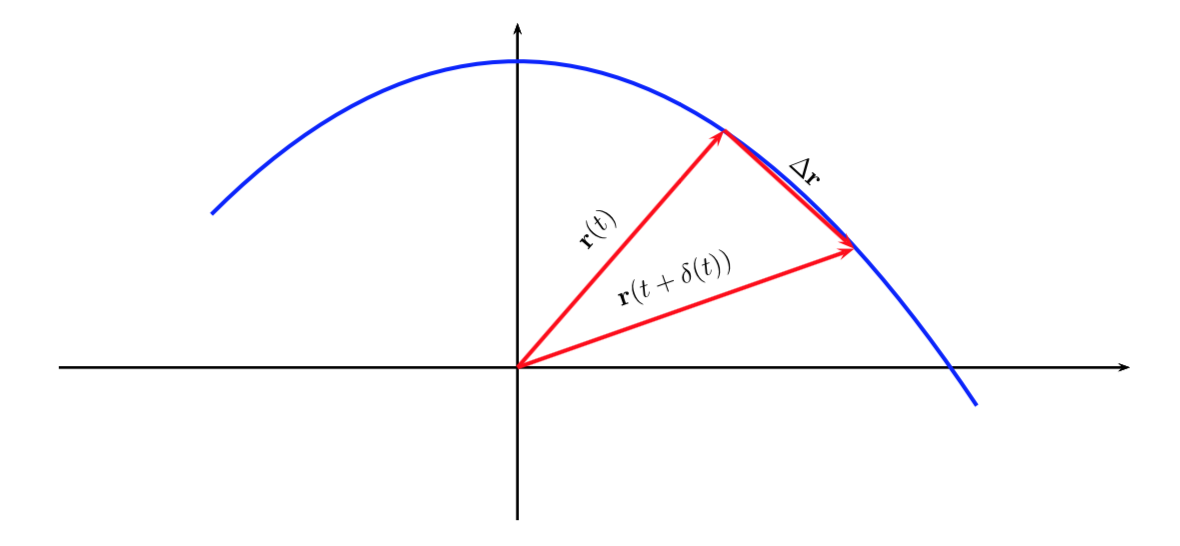
Il vettore posizione è un vettore che inizia nell’origine del sistema di riferimento e termina nel punto stesso. In generale se il punto materiale è in movimento il vettore posizione è una funzione variabile nel tempo. Nel piano possiamo esprimere il vettore posizione in funzione delle componenti rispetto agli assi cartesiani:
\[ \mathbf{r}(t)= x(t) \mathbf{i}+ y(t) \mathbf{j} \]1.2) Velocità
La velocità di un punto materiale che si muove nel piano è definita come la variazione del vettore posizione nell’unità di tempo. In simboli:
\[ \mathbf{v}(t) = \frac{d \mathbf{r}(t)}{dt} \]Anche la velocità è quindi un vettore e può essere decomposta nelle sue componenti lungo gli assi cartesiani:
\[ \mathbf{v}(t)= \frac{d x(t)}{dt} \mathbf{i}+\frac{d y(t)}{dt} \mathbf{j} \]1.3) Accelerazione
L’accelerazione di un oggetto è definita come la variazione del vettore velocità nell’unità di tempo. La velocità è un vettore, quindi ci può essere accelerazione perché varia il modulo della velocità o anche perché varia soltanto la direzione (come nel moto circolare uniforme). La definizione matematica dell’accelerazione è la seguente:
\[ \mathbf{a}(t)=\frac{d \mathbf{v}(t)}{dt} = \frac{d^{2}x(t)}{dt^{2}} \mathbf{i}+ \frac{d^{2}y(t)}{dt^{2}} \mathbf{j} \]Conoscendo l’espressione del vettore posizione nel tempo, possiamo calcolare la velocità e l’accelerazione mediante operazioni di derivazione. Viceversa, conoscendo l’espressione dell’accelerazione in funzione del tempo, possiamo calcolare la velocità e quindi la posizione nel tempo mediante operazioni di integrazione:
\[ \begin{split} \mathbf{v}(t) &= \int_{t_{0}}^{t} \mathbf{a}(t) dt \\ \mathbf{r}(t) &= \int_{t_{0}}^{t} \mathbf{v}(t) dt \\ \end{split} \]Esempio 1.1 – Moto uniformemente accelerato
Supponiamo che un corpo si muova con accelerazione costante \(\mathbf{a}\), e che al tempo \(t=0\) abbia velocità uguale a \(\mathbf{v}_{0}\) e si trovi nella posizione \(\mathbf{r}_{0}\). Applicando le due operazioni di integrazione sopra descritte otteniamo l’espressione per la velocità e la posizione in funzione del tempo:
Naturalmente queste equazioni vettoriali possono essere proiettate lungo gli assi cartesiani, ottenendo equazioni separate per le componenti della velocità e del vettore posizione.
Esempio 1.2
Un esempio di moto uniformemente accelerato è quello di un corpo che cade sotto l’azione della gravità terrestre. Trascurando la resistenza dell’aria, come vedremo in seguito, il corpo cade verso il basso con accelerazione costante \(a=g\), dove \(g=9,8 m s^{-2}\) è l’accelerazione di gravità, che possiamo considerare costante vicino alla superficie della Terra.
Sempre di moto uniformemente accelerato si tratta nel caso di un proiettile lanciato dall’origine di un sistema di riferimento cartesiano, con un vettore velocità iniziale \(\mathbf{v}=(v_{0,x},v_{0,y})\). Supponendo che sia presente solo la forza di gravità terrestre e trascurando la resistenza dell’aria, il proiettile percorre una traiettoria parabolica. Le equazioni sopra riportate permettono di calcolare il punto e il tempo nel quale il proiettile cade di nuovo a terra.
2) Dinamica
La dinamica studia il moto degli oggetti tenendo conto della massa e facendo una analisi completa delle forze in gioco. L’analisi dinamica permette di prevedere il moto degli oggetti sui quali agiscono le forze. Esempi tipici sono il moto degli oggetti sulla superficie terrestre sotto l’azione della gravità, il moto dei pianeti intorno al sole, o il calcolo del tempo necessario per frenare un’automobile che si muove ad una data velocità.
In questo articolo viene fatto un riepilogo dei principali concetti e delle equazioni della dinamica del moto. Tuttavia per uno studio approfondito rimandiamo ai testi di fisica, tra i quali in particolari i seguenti che sono eccellenti: [1], oppure [2].
2.1) Le forze
Il concetto di forza è fondamentale in fisica. Nello studio della meccanica, possiamo definire la forza come un’azione che tende a mantenere o modificare il moto di un oggetto. Esistono diversi tipi di forze. Una distinzione utile è quella fra le forze di contatto e le forze a distanza. Tra le principali forze a distanza ricordiamo:
- forza di attrazione gravitazionale
- forze elettrica
- forza magnetica
Le forze di contatto agiscono fra oggetti che si toccano fisicamente. Tra le forze a contatto ricordiamo le seguenti:
- attrito (ad esempio un corpo che rotola o striscia su una strada)
- resistenza dell’aria
- forza di reazione (ad esempio un oggetto su un tavolo)
- urti fra due particelle
Il modello delle forze di contatto è un’approssimazione utile nella risoluzione di molti problemi. Tuttavia a rigore, data la struttura atomica della materia, non c’è mai un vero contatto fisico fra i corpi e tutte le forze dovrebbero essere trattate come forze a distanza, anche se microscopica.
La forza è una grandezza vettoriale, che nel Sistema Internazionale si misura in Newton. Fissato un sistema di riferimento nel piano, una forza può essere decomposta nelle sue componenti secondo la direzione degli assi coordinati:
2.2) Le tre leggi della dinamica di Newton
Il concetto di forza è stato introdotto da Isacco Newton nella sua opera fondamentale “Philosophiae Naturalis Principia Mathematica”, pubblicata il 5 luglio 1687, nella quale sono descritte le sue famose tre leggi della dinamica.
Le tre leggi del moto di Newton sono le seguenti:
- legge di inerzia: in un sistema di riferimento inerziale, ogni corpo non soggetto a forze rimane nel suo stato di quiete o di moto rettilineo uniforme
- legge della forza: \(\mathbf{F}=m \mathbf{a}\)
- principio di azione-reazione: ad ogni azione corrisponde una reazione uguale e contraria
La prima legge era già stata formulata da Galileo e richiede di definire esattamente quali sono i sistemi di riferimento inerziali. Per questi concetti niente affatto semplici rimandiamo ai testi di fisica della bibliografia.
La seconda legge esprime la scoperta fondamentale che le forze sono la causa dei moti accelerati. Se su un oggetto di massa \(m\) viene esercita una forza \(\mathbf{F}\), allora il corpo subisce un’accelerazione del valore \(\mathbf{a}=\frac{\mathbf{F}}{m}\).
La forza è responsabile dell’accelerazione di un corpo materiale. Il movimento a velocità costante è possibile senza che ci siano forze in gioco, contrariamente a quanto credevano i filosofi dell’antichità, come Aristotele.
La terza legge implica che se un oggetto esercita una forza su un altro oggetto (ad esempio un libro posto sopra il tavolo esercita una pressione sul tavolo), allora il secondo oggetto esercita una reazione uguale e contraria sul primo oggetto (il tavolo esercita una forza uguale e opposta sul libro).
2.3) Legge di gravitazione universale di Newton
Un esempio importante di applicazione delle leggi di Newton è il calcolo delle traiettorie dei pianeti e dei satelliti nel sistema solare. La legge di gravitazione universale scoperta da Newton afferma che dati due corpi di masse \(m,M\) rispettivamente, che si trovano a distanza \(r\), tra di essi si esercita una forza di attrazione gravitazionale la cui grandezza è espressa dalla seguente formula:
\[ \mathbf{F} = G \frac{mM}{r^{2}} \mathbf{u_{r}} \]dove \(G= 6,67 \cdot 10^{-11} m^{3} (Kg)^{-1} s^{-2}\) è la famosa costante di gravitazione universale. Il vettore \(\mathbf{u_{r}}\) è un vettore di modulo unitario, con direzione uguale al raggio vettore che congiunge i due punti materiali.
A causa del valore della costante \(G\), la forza gravitazionale è molto debole se le masse in gioco non sono grandi. Per gli oggetti che stanno vicino alla superficie della Terra la formula di Newton può essere semplificata in questo modo:
dove \(g=9,8 ms^{-2}\) è il valore costante dell’accelerazione e la direzione è perpendicolare alla superficie della terra. In sostanza vicino alla superficie della Terra la forza di gravità non dipende dalla distanza fra il corpo e la Terra; tutti i corpi, di qualsiasi massa, subiscono la stessa accelerazione, trascurando la resistenza dell’aria e altre eventuali forze.
Esempio 2.1 – Moto di un proiettile
Un proiettile viene lanciato dall’origine di un sistema di riferimento cartesiano, con un vettore velocità iniziale \(\mathbf{v}=(v_{0,x},v_{0,y})\). Supponendo che sia presente solo la forza di gravità terrestre e trascurando la resistenza dell’aria, il proiettile percorre una traiettoria parabolica. Le leggi di Newton permettono di calcolare completamente la traiettoria dal punto di vista spaziale e temporale. La traiettoria è una parabola le cui equazioni parametriche sono le seguenti (supponiamo di sparare il proiettile dal punto di coordinate \( (x_{0},y_{0})\)):
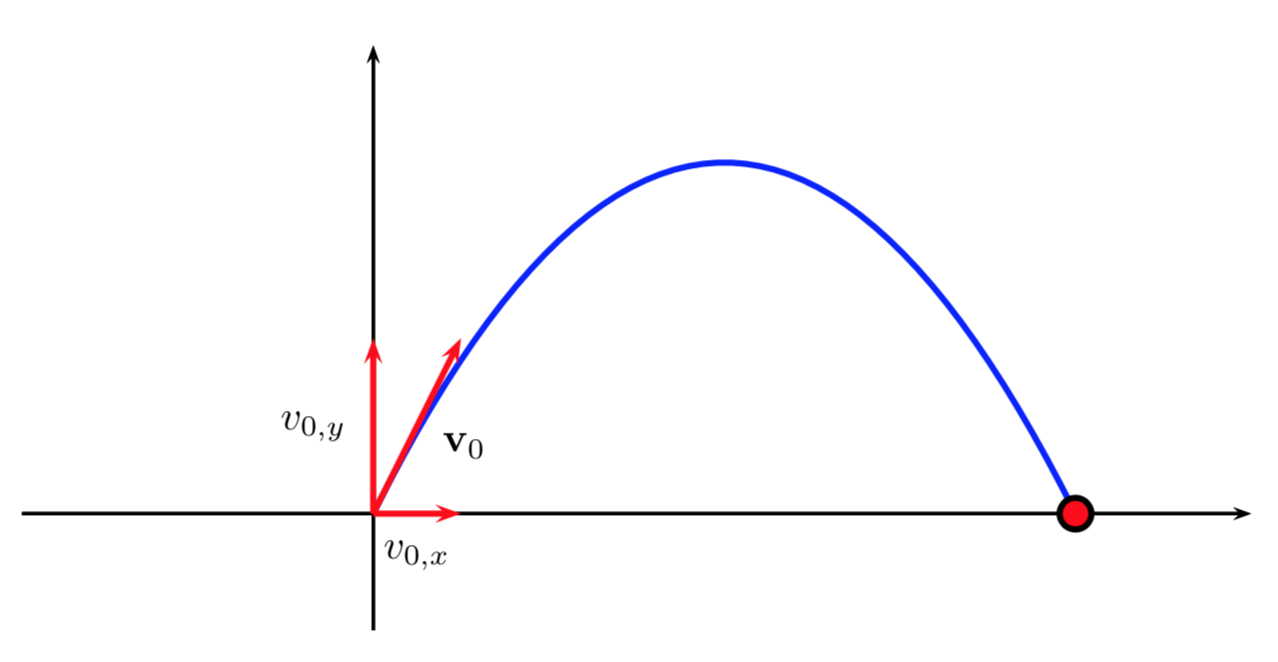
Alcune formule importanti derivate dalle equazioni del moto sono le seguenti (indichiamo con \(v_{0}\) il modulo del vettore velocità al tempo \(t=0\) e con \(\alpha\) l’angolo della velocità iniziale con l’asse delle ascisse \(x\)):
\[ \begin{split} \textbf {accelerazione orizzontale} &= a_{x}=0 \\ \textbf {accelerazione verticale} &= a_{y}=-g \\ \textbf {velocità orizzontale} &= v_{x}(t) = v_{0,x} \\ \textbf {velocità verticale} &= v_{y}(t) = v_{0,y} – gt \\ \textbf {massima altezza} &= \frac {v_{0}^{2} (\sin \alpha)^{2}}{2g} \\ \textbf {tempo di ritorno a terra} &= \frac {2v_{0}\sin \alpha}{g} \\ \textbf{gittata} &= \frac {v_{0}^{2} (\sin 2\alpha)}{g} \\ \end{split} \]Esercizio 2.1
Dimostrare che, trascurando la resistenza dell’aria, l’angolo di massima gittata per un cannone è di \(45^{\circ}\).
3) Principi di conservazione
È utile accennare ad alcuni dei principi di conservazione, che oltre ad avere un significato profondo dal punto di vista fisico, sono molto utili nella risoluzione dei problemi di fisica.
3.1) Principio di conservazione dell’energia
Esistono diversi tipi di energia: energia cinetica, energia potenziale, energia termica, energia nucleare, ecc. La somma totale di tutte questi tipi di energie si mantiene costante nell’universo; l’energia non può essere distrutta o creata, ma può solo essere trasformata da una forma all’altra. Quando si studia un fenomeno fisico è utile suddividere l’universo in due parti separate: il sistema che si sta studiando e l’ambiente circostante. Se questi due sistemi si scambiano energia o massa allora l’energia del sistema in studio può non conservarsi.
Il principio di conservazione dell’energia è un principio generale che vale senza eccezioni. Nei problemi di meccanica vale un principio più ristretto, il principio di conservazione dell’energia meccanica, che include solo i tipi di energia che interessano il contesto fisico, l’energia cinetica e l’energia potenziale.
3.2) Energia cinetica
L’energia cinetica è energia dovuta al movimento degli oggetti. Un corpo di massa \(m\) che si muove a velocità di grandezza \(v\), ha una energia cinetica data dalla seguente formula:
\[ \text {Energia cinetica} = K = \frac{1}{2}m v^{2} \]Le dimensioni dell’energia cinetica sono \(ML^{2}T^{-2}\). L’unità di misura nel SI è il Joule: \( 1 \text {Joule } = 1 Kg \cdot m^{2} \cdot s^{-2}\).
3.3) Energia potenziale
L’energia potenziale è un tipo di energia dovuto alla possibilità di compiere lavoro spostando un corpo da una posizione all’altra, in presenza di un campo di forza. Un corpo possiede energia potenziale per il fatto che può compiere un lavoro. Ad esempio un corpo di massa \(m\) che si trova ad altezza \(h\) sopra la superficie terrestre, se lasciato cadere trasforma la sua energia potenziale in energia cinetica, che può essere utilizzata per compiere lavoro. Viceversa per portare un corpo dalla superficie terrestre ad un’altezza \(h\) bisogna compiere lavoro per contrastare la forza di gravità.
La formula per l’energia potenziale di un corpo di massa \(m\) che si trova ad altezza \(h\) dalla superficie terrestre è la seguente:
3.4) Energia meccanica
La forza gravitazionale ha una proprietà molto importante: il lavoro compiuto per portare un corpo da un’altezza ad un’altra non dipende dal cammino percorso, ma soltanto dal punto iniziale e dal punto finale. In fisica si dice che la forza gravitazionale è una forza conservativa.
L’energia meccanica \(E\) è definita come la somma dell’energia cinetica e dell’energia potenziale:
Il principio di conservazione dell’energia meccanica afferma che, in un sistema chiuso e in assenza di forze dissipative (come l’attrito o la resistenza dell’aria), l’energia meccanica totale in un campo di forze conservativo si mantiene costante. Quindi l’energia potenziale può trasformarsi in energia cinetica, e viceversa, ma la somma delle due rimane costante.
3.5) Principio di conservazione della quantità di moto
Un’altra grandezza fisica importante è la quantità di moto di un punto materiale di massa \(m\) che si muove a velocità \(\mathbf{v}\):
\[ \text{Quantità di moto} = \mathbf{p}= m \mathbf{v} \]È una grandezza vettoriale per la quale vale il seguente principio di conservazione: in un sistema isolato, la quantità di moto totale di un insieme di punti materiali viene conservata.
Ad esempio nella collisione fra due corpi materiali, la quantità di moto totale prima dell’urto è uguale alla quantità di moto totale dopo l’urto.
3.6) Impulso e quantità di moto
Un’altra grandezza importante è l’impulso che acquista un corpo di massa \(m\), sottoposto ad una forza \(F\) per un certo intervallo di tempo \(\Delta t\). Usiamo il simbolo \(\mathbf{J}\) per indicare l’impulso. La legge fondamentale da ricordare è espressa dalla seguente formula:
\[ \text {Impulso} = \mathbf{J}= \int_{t_{1}}^{t_{2}} F(t)dt = \mathbf{p_{2}} – \mathbf{p_{1}} \]Quindi l’impulso applicato da una forza nell’intervallo di tempo \([t_{1},t_{2}]\) è uguale alla variazione della quantità di moto subita dal corpo di massa \(m\) sul quale agisce la forza.
Per un approfondimento di questi concetti abbastanza complessi, consultare i testi di fisica suggeriti nella bibliografia.
4) Il motore fisico Unity Physics 2D
Gli oggetti (GameObjects) che interagiscono nella scena sono identificati ognuno dalle coordinate cartesiane (x,y,z) nello spazio 3D, oppure dalle (x,y) in 2D. Per simulare il mondo reale è necessario per ogni oggetto applicare le leggi della fisica ed effettuare i calcoli necessari per determinare la velocità, l’accelerazione, la frequenza di rotazione, il risultato degli urti con altri oggetti, ecc.
Nelle versioni più recenti di Unity è stato aggiunto un componente per la simulazione delle leggi della fisica degli oggetti sulla scena 2D, il motore fisico Physics 2D. I parametri del motore Physics 2D vengono impostati mediante il Physics 2D manager (Edit > Project Setting > Physics2D).
Ricordiamo che i motori fisici Unity 2D e 3D sono completamente separati. Il motore 3D utilizza il prodotto software PhysX, mentre il motore 2D utilizza Box2D.
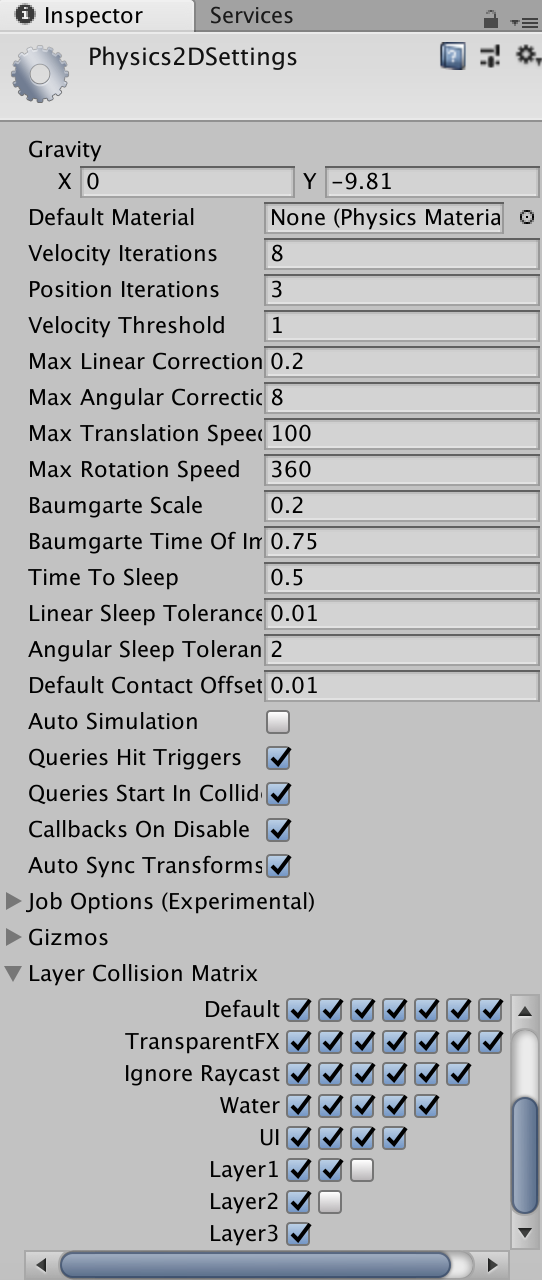
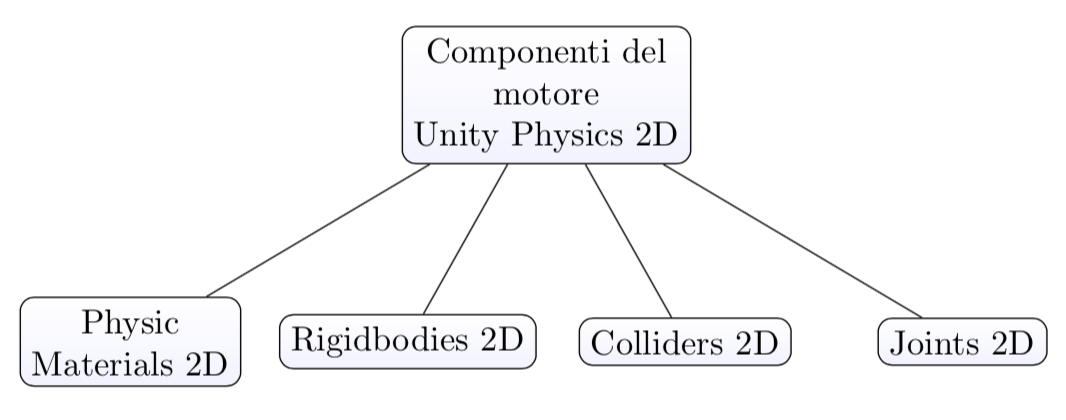
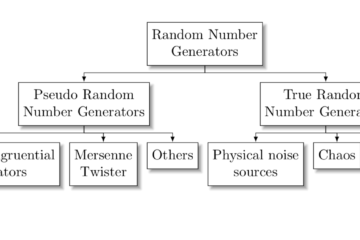
4.1) Componenti del motore fisico Physics 2D
I principali componenti del Physics 2D sono illustrati nel seguente diagramma:
4.2) Il componente Collider 2D
In Unity 2D le collisioni non sono definite direttamente dal Rigidbody 2D, ma da nuovi componenti chiamati Collider 2D. Si tratta di componenti che definiscono una regione del piano nella quale può verificarsi l’interazione fra gli oggetti. Queste regioni in genere hanno una forma diversa dagli oggetti stessi, tranne nei casi di oggetti di forma geometrica semplice. I principali componenti Collider 2D sono illustrati nel seguente diagramma:
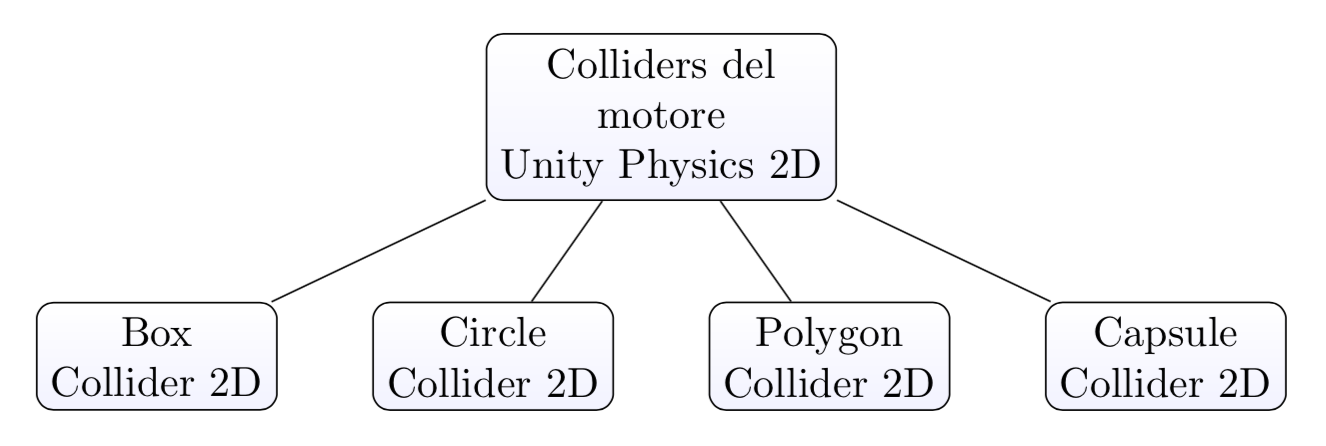
L’argomento delle collisioni 2D è stato illustrato in un precedente articolo di questo blog.
4.3) Il componente Rigidbody 2D
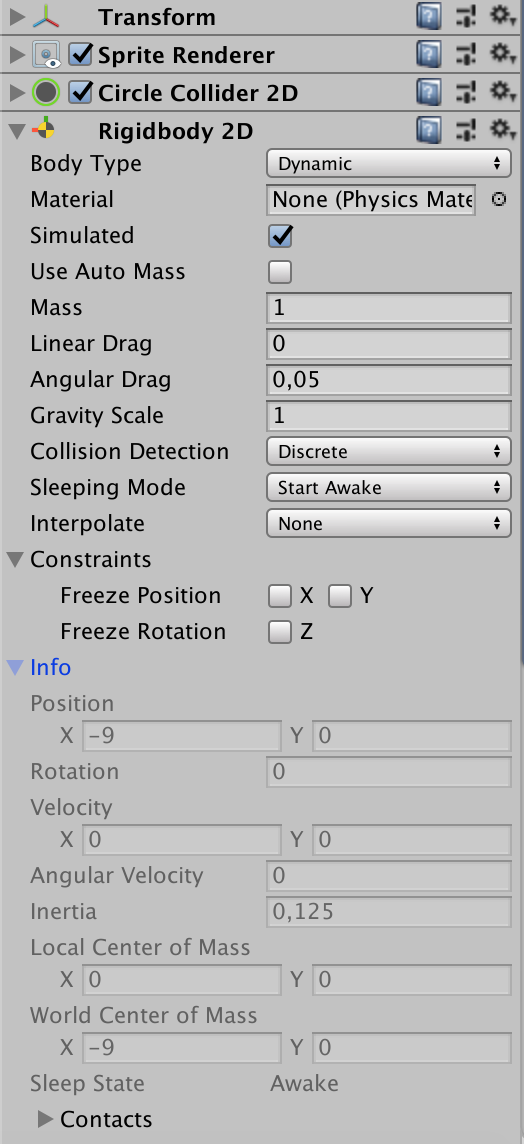
Il componente Rigidbody2D permette di simulare le interazioni fisiche fra gli oggetti. Un oggetto (ad esempio uno sprite) cui è associato il componente Rigidbody2D viene messo sotto il controllo del motore fisico Physics 2D. Il componente Rigidbody2D definisce le proprietà fisiche quali l’intensità della gravità, la massa, l’attrito, ecc. Gli oggetti Rigidbody 2D possono muoversi solo nel piano XY e possono ruotare intorno all’asse Z. Esiste la possibilità di annullare gli effetti della gravità per l’intera scena (Edit>Project Settings>Physics 2D), oppure per un singolo oggetto, aggiornando il componente Rigidbody2D.
Ci sono tre opzioni per il Body Type, che definiscono tre diverse modalità di comportamento:
- Dynamic
- Kinematic
- Static
L’opzione Dynamic implica che l’oggetto si muove sotto il controllo del motore fisico, in funzione delle proprietà definite nel componente Rigidbody 2D (massa, drag, scala della gravità, ecc).
L’opzione Kinematic implica che l’oggetto si muove nel contesto della simulazione fisica, però il controllo è lasciato all’applicazione. Per un oggetto con l’opzione Kinematic il moto non è influenzato dalla massa, dalla gravità o da altri tipi di forze, come invece è con l’opzione Dynamic.
Con l’opzione Static un oggetto non si muove sotto la simulazione fisica; in una collisione si comporta come un oggetto di massa infinita, che non si sposta.
Nel paragrafo successivo descriveremo le possibilità che il componente Rigidbody 2D offre per simulare il moto di oggetti nell’ambiente 2D.
4.4) Il materiale fisico 2D (Physics Material 2D)
Il materiale fisico 2D è un componente che può essere associato ad un GameObject per definire le caratteristiche fisiche dell’oggetto stesso. Il materiale fisico contiene due proprietà: Bounciness (quanto l’oggetto rimbalza dopo un urto) e Friction (l’attrito). Una scelta corretta permette di simulare con maggiore precisione il comportamento di oggetti reali nei processi fisici, ad esempio nelle collisioni con altri oggetti.
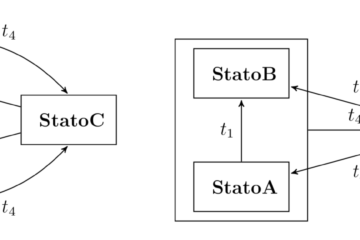
4.5) Il tipo Joint e le sue proprietà
I Joints 2D (giunture) sono componenti che permettono di definire dei vincoli fisici fra due oggetti, con vari gradi di libertà. Questo permette di simulare la fisica anche per oggetti composti da vari componenti, come porte, veicoli, strutture complesse di vario tipo. I principali tipi di joints offerti da Unity 2D sono illustrati nel seguente diagramma:
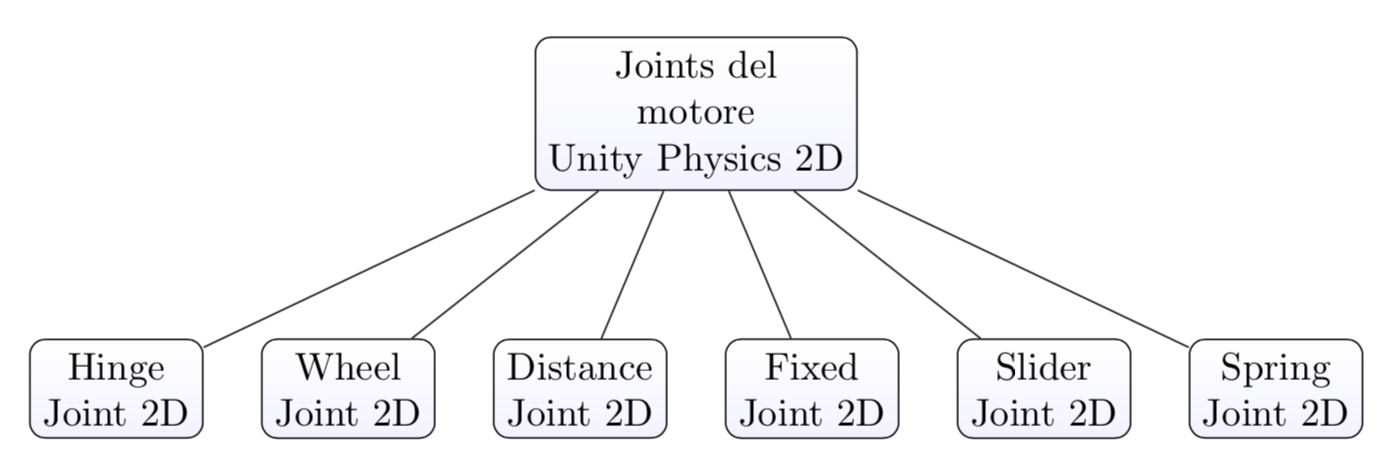
- Fixed Joint – lega due oggetti in modo rigido, simile ad una relazione parent -> child. Il corpo con il Fixed Joint segue i movimenti dell’altro oggetto. In presenza di ostacoli può succedere che non riesca a mantenere la distanza fissa, ma può assumere un comportamento simile ad una molla
- Hinge Joint – usato ad esempio per creare una porta a battenti. È come una giuntura a cardine, come un cardine di una porta
- Distance Joint – permette di stabilire una certa distanza fra due oggetti
- Wheel Joint – simula il comportamento di una ruota, per permettere la creazione di veicoli di vario genere
- Slider Joint – permette di creare una sorta di binario sul quale un corpo può scorrere
- Spring Joint – simula il comportamento di una molla
Modalità di creazione di un Joint in Unity 2D
La modalità di creazione di un Joint è simile per tutti i tipi; cambiano soltanto alcuni parametri specifici da impostare. I passi principali per definire un joint fra due oggetti sono i seguenti:
- creare un oggetto e assegnargli il componente Rigidbody2D
- assegnare un materiale fisico all’oggetto
- aprire il menù dei Joints (Component -> Physics2D)
- scegliere il tipo di Joint
- impostare i parametri nell’Inspector
- impostare il campo Connected Body trascinando il secondo oggetto da collegare
L’animazione seguente rappresenta uno Spring joint, che simula l’oscillazione di un pendolo:
5) Il moto con il motore Unity Physics 2D
Come è noto in Unity le informazioni sulla posizione, rotazione e scala degli oggetti sulla scena vengono gestite normalmente tramite il componente Transform associato ad ogni oggetto.
Mediante il componente Rigidbody2D è possibile mettere gli oggetti sotto il controllo del motore fisico, il quale a sua volta può modificare la posizione e la velocità degli oggetti stessi. Un compito fondamentale del componente Rigidbody2D è proprio quello di gestire la comunicazione con il componente Transform al fine di rendere i dati sulla posizione sempre aggiornati correttamente. Il componente Rigidbody2D offre alcune proprietà e funzioni che permettono di controllare il moto di un corpo, simulando una forza applicata all’oggetto:
- Rigidbody2D.velocity
- Rigidbody2D.MovePosition
- Rigidbody2D.AddForce,ForceMode2D=Force
- Rigidbody2D.AddForce,ForceMode2D=Impulse
La funzione AddForce accetta due parametri: il primo indica il vettore (Vector2D) che rappresenta la forza applicata e il secondo che indica il tipo di spinta (ForceMode2D). Sono previsti due tipi di spinte:
- impulso (forza applicata per un breve intervallo di tempo, ad esempio per effettuare un salto)
- continua (è una forza normale, come la spinta per muovere un carro o il motore di un auto)
Le funzioni che utilizzano il motore fisico devono essere messe nel metodo FixedUpdate, poiché è quella la frequenza con cui Unity aggiorna i calcoli per la simulazione della fisica.
5.1) Il moto con Rigidbody2D.velocity
Questa funzione applica una variazione istantanea di velocità del Rigidbody2D, ignorando la sua massa. Per capire la differenza con AddForce supponiamo di avere un oggetto che si muove in una certa direzione. Se applichiamo una forza in direzione perpendicolare alla direzione del moto, l’oggetto non farà un cambiamento improvviso di \(90^{\circ}\), ma il cambiamento di direzione avverrà in modo graduale, in funzione dell’intensità della forza. Ad ogni intervallo di tempo viene fatta la somma vettoriale fra il vettore velocità e il vettore forza, calcolando la nuova direzione del moto. Invece applicando la funzione Rigidbody2D.velocity si ha un cambiamento istantaneo di direzione. Ad esempio se un oggetto si sta muovendo lungo la direzione positiva dell’asse \(X\), eseguendo la seguente istruzione:
rigidbody2D.velocity = Vector2.up;avremo un cambiamento improvviso del moto verso la direzione positiva dell’asse \(Y\).
L’immagine seguente illustra il movimento di una palla lanciata per colpire un oggetto target che si sposta dopo ogni collisione. Ogni volta viene calcolata la velocità iniziale necessaria, in base alle leggi della dinamica, per colpire il target. La palla è associata naturalmente al componente Rigidbody2D con il Body Type impostato a Dynamic.

Uno schema di massima delle istruzioni per calcolare la velocità di lancio del proiettile è il seguente:
void PartenzaProiettile() {
Vector2 m_veloStart =
CalcolaVelocitaIniziale(transform.position,
target.transform.position);
m_Rigidbody2D.velocity = m_veloStart;
}
// calcola la velocità iniziale del proiettile
public Vector2 CalcolaVelocitaIniziale(Vector2 origine,
Vector2 target) {
float gravity = Physics2D.gravity.magnitude;
float distanza = Mathf.Abs(target.x - origine.x);
float altezzaMax = distanza / 4;
float velInizialeY = Mathf.Sqrt(2.0f * gravity *
altezzaMax);
float time = (velInizialeY + Mathf.Sqrt(velInizialeY *
velInizialeY - 2*gravity * target.y))/gravity;
float velInizialeX = distanza / time;
// direzione a destra
if (target.x - origine.x > 0.0f){
return new Vector2(velInizialeX, velInizialeY);
}
// direzione a sinistra
else {
return new Vector2(-velInizialeX, velInizialeY);
}
}5.2) Moto con Rigidbody2D.MovePosition
Oltre alla proprietà Rigidbody2D.velocity, esiste anche un’altra funzione che si può utilizzare per modificare la posizione di un oggetto: Rigidbody2D.MovePosition. Il metodo MovePosition ha un effetto simile, tranne che il Rigidbody2D deve essere impostato a Kinematic. In questo caso la posizione viene aggiornata ad ogni frame fisso e la velocità viene calcolata internamente dal motore fisico. La funzione MovePosition è utile per inseguire un altro oggetto in movimento. La seguente animazione illustra un oggetto che insegue un target che si muove di moto circolare.

Le istruzioni per inseguire on oggetto target sono le seguenti (l’opzione “Gravity scale” è impostata a zero):
private void FixedUpdate() {
Vector2 direction = (target.transform.position -
transform.position).normalized;
if (Vector2.Distance(target.transform.position,
transform.position) > minDist)
{
m_Rigidbody2D.MovePosition(m_Rigidbody2D.position +
direction * speed * Time.fixedDeltaTime);
}
else
{
Debug.Log("Target raggiunto ");
}5.3) Moto con Rigidbody2D.AddForce (ForceMode.Force)
Con la funzione AddForce la forza viene applicata durante ogni intervallo fisso (timestep) di tempo dal motore fisico. Il valore di default è 0,02 sec, ma può essere modificato tramite l’editor (Edit->Project->Settings->Time).
Il metodo AddForce con il parametro ForceMode2D.Force, applica una forza continua graduale sull’oggetto, durante il periodo del frame, e tiene conto della massa.
5.4) Moto con AddForce (ForceMode.Impulse)
Il metodo AddForce con il parametro ForceMode2D.Impulse, applica una forza istantanea sull’oggetto, e tiene conto della massa. L’impulso dura per tutto l’intervallo del frame. È usata ad esempio per simulare esplosioni.
Per l’elenco completo delle proprietà del componente Rigidbody vedere la sezione corrispondente del manuale Unity.
5.5) Un esempio di moto orbitale con AddForce
Nell’animazione seguente simuliamo il moto di un pianeta intorno al sole. Viene applicata la legge di gravitazione universale con opportune operazioni di scalamento delle grandezze in gioco. Entrambi gli oggetti hanno il componente Rigidbody2D, con tipo Dynamic. Il Gravity Scale è impostato a zero.

private void FixedUpdate() {
Vector2 forzaApplicata = Vector2.zero;
Vector2 distanza = (target.transform.position -
transform.position) * scalaDistanza;
float distQuadrato = distanza.sqrMagnitude;
// utilizza legge di Newton
float forzaGrav = G * m_Rigidbody.mass *
m_RigidbodyTarget.mass / distQuadrato;
forzaApplicata = forzaGrav * distanza.normalized;
m_Rigidbody.AddForce(forzaApplicata,ForceMode2D.Force);
}6) Rotazioni in 2D
Per concludere accenniamo ad un’altra funzione messa a disposizione per effettuare le rotazioni nel piano: RigidBody2D.AddTorque. Il Torque è il momento che una forza esercita su un corpo rispetto ad un punto di riferimento. Il momento di una forza applicata ad un punto materiale che si trova nella posizione \(P\), rispetto ad un punto iniziale \(O\) è così definito:
\[ \mathbf{M} = \mathbf{r} \times \mathbf{F} = (rF \sin \theta) \mathbf{u} \]dove \(\mathbf{r}\) è il raggio vettore \(\mathbf{OP}\), che va dal punto origine \(O\) alla posizione \(P\) dove si trova il punto materiale, e \(\mathbf{u}\) è il versore di direzione perpendicolare al piano formato da \(\mathbf{r}\) e \(\mathbf{F}\). Il momento è causa della rotazione di un corpo. L’argomento delle rotazioni nel piano verrà discusso in un successivo articolo.
Conclusione
Molti videogiochi per dispositivi mobili o anche per desktop sono ancora sviluppati nell’ambiente 2D. È quindi importante conoscere le funzionalità che la piattaforma Unity offre, e tra queste in particolare le potenzialità del motore Physics2D per gestire il movimento e le collisioni fra gli oggetti.
Bibliografia
[1]Halliday, Resnick – Fundamentals of Physics (Wiley)
[2]R. Feynman – The Feynman Lectures on Physics (Basic Books)

0 commenti