Il matematico francese Bertrand (1822-1900) formulò la congettura che per ogni intero positivo \(n\) esiste sempre almeno un numero primo \(p\) tale che: \(n < p \le 2n\).
Questa congettura venne dimostrata dal matematico russo Chebyshev (1821- 1894). In questo articolo illustreremo il metodo di dimostrazione proposto dal matematico ungherese Erdos (1913-1996), che è basato su alcune proprietà dei coefficienti binomiali e non richiede gli strumenti più avanzati dell’analisi matematica. Alla fine accenneremo ad una dimostrazione molto breve proposta dal matematico indiano Ramanujan e studieremo una categoria di numeri primi introdotti dallo stesso Ramanujan, che hanno proprietà interessanti.
1) Introduzione
Ricordiamo inizialmente alcune proprietà elementari dei numeri primi. Introduciamo la funzione aritmetica \(\pi(x)\) che conta il numero dei primi minori od uguali a \(x\):
\[ \pi(x) = | \{p \in \mathbb{P}: p \le x \}| \]dove \(\mathbb{P}\) è l’insieme dei numeri primi \(\{2,3,5,7, \cdots \}\) e \(x\) è un numero reale positivo.
Teorema 1.1
Esistono infiniti numeri primi. Quindi \(\lim_{x \to \infty}\pi(x) = \infty\).
Esistono diverse dimostrazioni sul numero infinito dei numeri primi, a partire da quella famosa ed elegante di Euclide (vedere link su questo blog). Riportiamo di seguito una dimostrazione basata sulle proprietà della funzione di Eulero (link), che come è noto è una funzione moltiplicativa. Sappiamo che se \(n=p_1^{a_1}\cdots p_k^{a_k}\), allora
\[ \varphi(n)=\prod_{i=1}^k p_i^{a_i-1}(p_i-1) = n \cdot \prod_{i=1}^{k} \left( 1- \frac{1}{p_{i}}\right) \]Supponiamo ora di avere una lista di \(k\) numeri primi \(p_{1}, \cdots p_{k}\), e sia \(n = \prod_{i=1}^{k} p_{i}\) il loro prodotto. Allora abbiamo
\[ \varphi(n) = \prod_{i=1}^{k} (p_{i}-1) \ge 2^{k-1}\ge 2 \]purché \(k \ge 2\). Da questa disuguaglianza possiamo dedurre che esiste un intero nell’intervallo \([2,n]\) che è primo con \(n\), che però ha un fattore primo distinto da tutti i primi \(p_{i}\) della lista.
Teorema 1.2 – Teorema fondamentale dell’aritmetica
Ogni intero \(n>1\) può essere scritto in modo univoco nella forma
dove \(k\) è un intero positivo, gli \(a_i\) sono interi positivi e \(p_1,p_2,\cdots p_k\) sono numeri primi che soddisfano la relazione \( p_1 < p_2 < \cdots < p_k\).
La dimostrazione si trova in ogni testo elementare di Teoria dei Numeri. Ad esempio vedere [1].
Esercizio 1.1
Sia \(\{p_{1},p_{2}, \cdots p_{k}, \cdots \}\) la successione dei numeri primi in ordine crescente. Dimostrare la seguente disuguaglianza:
Dimostrazione per induzione
L’affermazione è vera per \(n=1\) in quanto \(p_{1}=2\). Supponiamo che sia \(p_{n} < 2^{2^{n}} \). Allora il numero intero \(x=p_{1}p_{2} \cdots p_{n}+1\) ha un divisore primo diverso da \(p_{1}, \cdots p_{n}\). Quindi
dove abbiamo utilizzato la formula della somma geometrica. Quindi l’affermazione è vera per ogni \(n\).
Esercizio 1.2
Dimostrare che esistono intervalli grandi a piacere senza numeri primi.
Suggerimento
Basta prendere i numeri compresi nell’intervallo \([n!+2,n! +n]\).
2) Il fattoriale e la sua scomposizione in fattori primi
La scomposizione in fattori primi del fattoriale ha un ruolo importante nella dimostrazione di alcuni teoremi riguardanti la distribuzione dei numeri primi. Ricordiamo la definizione del fattoriale di un numero intero \(n\):
\[ \begin{align} n! = \begin{cases} n\cdot (n-1)! & \text{se n > 0} \\ 1 & \text{se n = 0} \\ \end{cases} \end{align} \]Teorema 2.1 – Legendre-de Polignac
La decomposizione canonica in fattori primi di \(n!\) è:
dove il numero intero \(r\) è tale che \( p^{r} \le n < p^{r+1}\).
Dimostrazione
Per ogni numero primo \(1 < p \le n\) dobbiamo calcolare l’esponente nella decomposizione in fattori primi. La somma
contiene un numero finito di termini non nulli. Il primo termine conta i multipli di \(p\), che sono i seguenti:
\[ 1 \cdot p, 2 \cdot p, \cdots ,\Bigl\lfloor \frac{n}{p} \Bigr \rfloor \cdot p \]Alcuni termini di \(n!\) sono divisibili anche per \(p^{2}\) e il numero di questi è dato dal secondo termine. Proseguendo, abbiamo che la somma coincide proprio con l’esponente del numero primo \(p\) nella fattorizzazione di \(n!\). Naturalmente la somma contiene solo un numero finito di termini non nulli; infatti, se \(k > r\) dove \(p^{r} \ge n\) allora il termine \(\Bigl\lfloor\frac{n}{p^{k}}\Bigr\rfloor=0\).
Osservazione
Il più grande esponente di un primo \(p\) nella fattorizzazione di un intero \(n\) viene indicato in genere con il simbolo \(\nu_{p}(n)\). Utilizziamo il simbolo \(\alpha (n,p)\) al posto di \(\nu_{p}(n!)\) perché risulta più comodo in questo contesto.
Esercizio 2.1
Se \(n=p^{k}\) dimostrare che \(\nu_{p} (p^{k}!) = \alpha (p^{k},p)=\frac{n-1}{p-1}\)
Esercizio 2.2 (Legendre, 1808)
Sia \(n=a_{k}p^{k}+a_{k-1}p^{k-1}+ \cdots + a_{1}p+a_{0}\) la decomposizione di \(n\) secondo la base \(p\). Dimostrare la seguente relazione:
Suggerimento
Considerare la seguente relazione:
dove \(R\) è una grandezza numerica \(<1\) se \(0 \le r <k\) in quanto tutte le cifre \(a_{i}\) sono inferiori a \(p\), e quindi la sua parte intera è uguale a zero. Da questo si può procedere effettuando dei calcoli un pò laboriosi ma non difficili.
3) I coefficienti binomiali
Come è noto il coefficiente binomiale \(\binom{n}{k}\), dove \(n,k\) sono interi positivi rappresenta il numero delle combinazioni semplici di \(n\) oggetti presi a \(k\) a \(k\), o in modo equivalente è il numero dei sottoinsiemi di ordine \(k\) che possono essere costruiti con \(n\) oggetti. Si definisce anche \(\binom{n}{0} = 1\). Si possono facilmente dimostrare le seguenti formule:
\[ \binom{n}{k}= \frac {n!}{k!(n-k)!} \] \[ \binom{n}{k}=\binom{n-1}{k} + \binom{n-1}{k-1} \]I coefficienti binomiali hanno un ruolo fondamentale in molti problemi di natura combinatoria. Ricordiamo ad esempio il Teorema del binomio di Newton:
\[ (x+y)^n = \sum_{k=0}^{n}\binom{n}{k} x^{k} y^{n-k} \]Un altro esempio importante è il Triangolo di Pascal-Tartaglia:
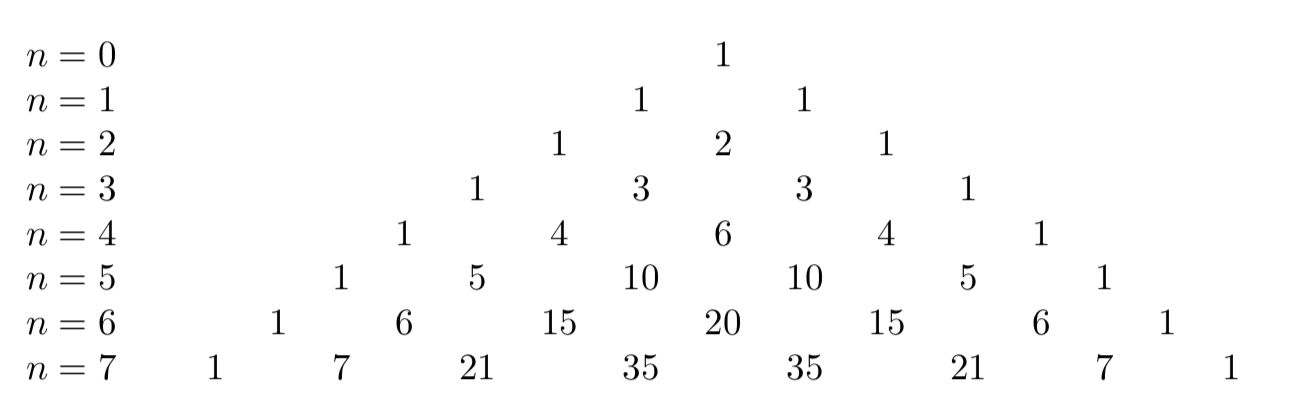
Ogni riga contiene i coefficienti dello sviluppo binomiale di Newton \((a+b)^{n}\). Ad esempio nella riga con n=6 appaiono i coefficienti binomiali \(\binom{6}{k}\), con \(\{k=0,1,2,3,4,5,6 \}\).
Esercizio 3.1
Se p è un numero primo dimostrare che
Esercizio 3.2
Dimostrare che \(\sum_{k=0}^{n}(-1)^{k}\binom{n}{k}=0\) .
Esercizio 3.3
Dimostrare la seguente identità:
Suggerimento
Utilizzare la seguente formula:
Esercizio 3.4
Dimostrare che se \(n\) è dispari e \(0 \le k \le n\) allora:
Soluzione
\[ 2^{n}=(1+1)^{n}= \sum_{k=0}^{n}\binom{n}{k}=2 \sum_{k=0}^{\frac{n-1}{2}}\binom{n}{k} \ge 2\binom{n}{k} \]Esercizio 3.5
Dimostrare che il massimo valore del coefficiente binomiale \(\binom{n}{k}\) viene raggiunto con \(k=\frac{n}{2}\) se \(n\) è un numero pari. Se \(n\) è dispari i valori massimi sono raggiunti con \(k=\frac{n-1}{2}\) e \(k=\frac{n+1}{2}\).
3.1) La scomposizione in fattori primi dei coefficienti binomiali
Il risultato trovato per la fattorizzazione del fattoriale ci permette di trovare la fattorizzazione del coefficiente binomiale. Utilizzando la formula \(\binom{n}{k}= \frac {n!}{k!(n-k)!} \), troviamo la seguente espressione per l’esponente di un numero primo \(p\) nella fattorizzazione del coefficiente binomiale \(\binom{n}{k}\):
\[ \begin{split} \beta(n,k,p) &= \alpha (n,p) – \alpha (k,p) – \alpha (n-k,p) =\\ &= \sum_{i=1}^{r} \left(\Bigl\lfloor \frac{n}{p^{i}}\Bigr \rfloor – \Bigl\lfloor \frac{k}{p^{i}}\Bigr \rfloor – \Bigl\lfloor \frac{n-k}{p^{i}}\Bigr \rfloor \right) \end{split} \]Abbiamo quindi il seguente teorema:
Teorema 3.1
La decomposizione canonica del coefficiente binomiale \(\binom{n}{k}\) è la seguente:
dove il numero intero \(r\) è tale che \( p^{r} \le n < p^{r+1}\).
3.2) Il coefficiente binomiale centrale
Ai fini della dimostrazione del postulato di Bertrand è utile studiare le proprietà del coefficiente binomiale centrale \(C_{n}\):
\[ C_{n} = \binom{2n}{n}=\frac{(2n)(2n-1) \cdots (n+2)(n+1)}{n!} \]L’esponente \(\beta (2n,n,p)\) in questo caso si semplifica:
\[ \begin{split} \beta(2n,n,p) &= \alpha (2n,p) – 2\alpha (n,p)=\\ &= \sum_{i=1}^{r} \left(\Bigl\lfloor \frac{2n}{p^{i}}\Bigr \rfloor – 2\Bigl\lfloor \frac{n}{p^{i}}\Bigr \rfloor\right) \end{split} \]dove \( p^{r} \le 2n < p^{r+1}\).
Esempio 3.1
La fattorizzazione di \(\binom{120}{60}\) è la seguente:
Esercizio 3.6
Dimostrare che \( \forall x \in \mathbb{R} si ha \lfloor 2x \rfloor – 2 \lfloor x \rfloor \in \{0,1 \}\).
Utilizzando l’esercizio precedente otteniamo facilmente una stima dall’alto del coefficiente binomiale centrale:
Teorema 3.2
\[ C_{n}=\binom {2n}{n} = \prod_{p \le 2n} p^{\beta(2n,n,p)}\le (2n)^{\pi (2n)} \]Una stima dal basso è espressa dal seguente teorema:
Teorema 3.3
Per tutti gli interi \(n > 0\) si ha:
Dimostrazione
\[ 4^{n}=(1+1)^{2n}=\sum_{k=0}^{2n}\binom{2n}{k}=2+ \sum_{k=1}^{2n-1}\binom{2n}{k} \le 2n \binom{2n}{n} \]Teorema 3.4
Nessuna delle potenze di primi della fattorizzazione di \(C_{n}\) supera \(2n\).
Dimostrazione
L’esponente relativo ad un fattore primo \(p\) è
Ogni termine della sommatoria ha valore massimo uguale a \(1\). Quindi la sommatoria ha valore \(\le 2n\), in quanto i termini della sommatoria sono tutti nulli se \(p^{k} > 2n\).
4) Il postulato di Bertrand
A questo punto possiamo completare gli ultimi passi necessari per dimostrare il postulato di Bertrand.
Teorema 4.1
Se un primo \(p \neq 2\) è tale che \( \frac{2n}{3} < p \le n\), allora \(p\) non divide \(C_{n}\).
Dimostrazione
Se \( \frac{2n}{3} < p \le n\) allora \(\lfloor \frac{2n}{p}\rfloor =2 \lfloor \frac{n}{p} \rfloor=2\) . Se \( n >4\) allora \(p^{k} > 2n\) per \( k \ge 2\). Lo stesso possiamo verificare per \( n \le 4\). Quindi non esistono numeri primi con esponenti positivi compresi nell’intervallo.
Definizione 4.1
Sia \(p_{i}\) la successione ordinata dei numeri primi. Chiamiamo il primoriale di \(n\) il seguente numero:
dove \(p_{k} \le n\) e \(p_{k+1} >n\)
Teorema 4.2
Per ogni intero positivo \(n\) si ha:
Dimostrazione
Il teorema è vero per \(n=1\) oppure \(n=2\). Dimostriamolo con il metodo di induzione. Supponiamo che sia vero per tutti gli interi \(k <n\) e dimostriamo che è vero anche per \(k=n\). Se \(n\) non è primo allora \(n\# = (n-1)\#\) e quindi per l’ipotesi \(n\# < 4^{n}\). Supponiamo quindi che \(n\) sia un primo dispari \(n=2m+1\). Sappiamo che il coefficiente binomiale
è divisibile da tutti i numeri primi \(p\) tali che \(m+2 \le p \le 2m+1\). Quindi
\[ \prod_{p \le 2m+1}p \le \binom{2m+1}{m} \prod_{p \le m+1}p < \binom{2m+1}{m} 4^{m+1} \]I due coefficienti binomiali \(\binom{2m+1}{m}\) e \(\binom{2m+1}{m+1}\) sono uguali e sono presenti nell’espansione binomiale di \((1+1)^{2m+1}\). Quindi
\[ \binom{2m+1}{m} \le \frac{1}{2}2^{2m+1}=4^{m} \]Mettendo insieme i risultati abbiamo infine
\[ \prod_{p \le 2m+1}p < 4^{m}4^{m+1}=4^{2m+1}=4^{n} \]Nota
Una forma alternativa del teorema precedente è la seguente:
dove \(x\) è un numero reale. Vedi [2].
A questo punto possiamo completare la dimostrazione del postulato di Bertrand.
Teorema 4.3 – Postulato di Bertrand
Per ogni intero \(n\), esiste un numero primo \(p\) tale che \(n < p \le 2n\)
Dimostrazione
Supponiamo che non esista alcun primo compreso fra \(n\) e \(2n\). Sappiamo che i fattori primi di \(C_{n}\) sono tutti minori o uguali a \(\frac{2n}{3}\).
Se \(n >4\) abbiamo la disuguaglianza \(\sqrt{2n} < \frac {2n}{3}\).
Dividiamo quindi i fattori primi di \(C_{n}\) in due gruppi: quelli che sono minori di \(\sqrt{2n}\) con prodotto \(P\) e quelli che sono compresi fra \(\sqrt{2n}\) e \(\frac{n}{3}\) con prodotto \(Q\); quindi \(C_{n}=P \cdot Q\).
I termini del prodotto \(P\) sono tutti inferiori a \(2n\) e quindi \(P \le (2n)^{\sqrt{2n}}\). I termini del prodotto \(Q\) hanno tutti esponenti uguali ad \(1\) come è facile verificare; quindi \(Q \le (\frac{2n}{3})\#\le 4^{(\frac{2n}{3})}\). Mettendo insieme con i risultati abbiamo:
Semplificando possiamo scrivere:
\[ 4^{\frac{n}{3}} \le (2n)^{1+ \sqrt{2n}} \]Questa disuguaglianza tuttavia non può essere vera per ogni valore di \(n\). Infatti si può vedere che il membro sinistro cresce più lentamente di quello destro all’aumentare di \(n\). Si può dimostrare che la disuguaglianza cessa di valere per \(n \ge 468\).
Senza esporre la dimostrazione rigorosa, ci si può convincere analizzando il grafico della funzione \(f(x)= 4^{\frac{x}{3}}- (2x)^{1+ \sqrt{2x}}\), ad esempio mediante il prodotto SageMathCell oppure con WolframAlpha. In particolare su WolframAlpha si può studiare il segno della funzione digitando il comando: (plot Sign(4^(x/3)- (2x)^(1+ \sqrt(2x))) from x=a to b).
Questa contraddizione implica che il postulato di Bertrand è vero almeno per \(n>467\). Tuttavia si può vedere facilmente che anche per valori inferiori il postulato è vero; basta trovare una successione di numeri primi ognuno dei quali è inferiore del doppio del precedente. Ad esempio la seguente
5) La dimostrazione di Ramanujan
Il matematico indiano Ramanujan (1887-1920) nel 1919 ha presentato un’altra dimostrazione elegante e molto breve, utilizzando strumenti di analisi più avanzati, come la formula di approssimazione di Stirling. Introduciamo alcune funzioni utilizzate nello studio della distribuzione dei numeri primi.
\[ \Lambda (n)= \begin{cases} \ln p \quad \text { se \(n=p^{k}\) con \(k \ge1\)} \\ 0 \quad \text{ altrimenti} \\ \end{cases} \] \[ \begin{split} \theta (x) = \sum_{p \le x} \ln p \\ \psi (x) = \sum_{n \le x} \Lambda (n) \\ \end{split} \]La funzione \(\Lambda (x)\) viene chiamata funzione di Mangoldt in onore del matematico tedesco H. Mangoldt(1854-1925). Le funzioni \(\theta(x)\) e \(\psi(x)\) vengono chiamate funzioni di Chebyshev, in onore del matematico russo P. Chebyshev.
Esercizio 5.1
Dimostrare la seguente formula:
Esercizio 5.2
\[ \begin{split} \Lambda (n) = \sum_{d|n} \mu (d) \ln \frac{n}{d} \\ \end{split} \] \[ \psi (x) = \sum_{k} \theta (x^{\frac{1}{k}}) \]Notiamo che \(x^{\frac{1}{k}} < 2 \) se \(k > \lfloor \frac{\ln x}{\ln 2}\rfloor\) e quindi \(\theta (x^{\frac{1}{k}})=0\).
Riportiamo soltanto alcuni passi della dimostrazione di Ramanujan; per i dettagli vedere [3].
La dimostrazione inizia con la formula
Da questa deriva la seguente:
\[ \ln [x]! – 2\ln [\frac{x}{2}]! = \psi(x) – \psi(\frac{x}{2})+ \psi(\frac{x}{3}) – \psi(\frac{x}{4}) \]Inoltre abbiamo
\[ \psi(x) – 2\psi (\sqrt{x}) = \theta(x) – \theta(x^{ \frac{1}{2}})+ \theta(x^{\frac{1}{3}}) – \theta(x^{\frac{1}{4}}) + \cdots \]Poiché le funzioni sono non decrescenti abbiamo le seguenti relazioni:
\[ \psi(x) – 2\psi (\sqrt{x}) \le \theta(x) \le \psi(x) \] \[ \psi(x) – \psi (\frac{1}{2}x) \le \ln [x]! – 2\ln [\frac{x}{2}]! \le \psi(x) – \psi(\frac{x}{2})+ \psi(\frac{x}{3}) \]A questo punto Ramanujan utilizza la formula di Stirling per l’approssimazione del fattoriale:
\[ \ln n! = n \ln n – n + O(\ln n) \]dove \(O(\ln n)\) è il simbolo di Landau (vedi link).
Con la formula di Stirling dimostra le seguenti relazioni:
Utilizzando le formule precedenti con pochi passi Ramanujan dimostra infine la seguente disuguaglianza:
\[ \theta (x) – \theta(\frac{x}{2}) > \frac{1}{6}x – 3 \sqrt{x} \text { se \(x >300\)} \]Poiché \(\frac{1}{6}x – 3 \sqrt{x} \ge 0\) se \( x \ge 324\) il risultato finale è
\[ \theta (2x) – \theta(x) > 0 \text { se \(x \ge 162\)} \]In altre parole c’è almeno un numero primo compreso fra \(x\) e \(2x\), se \(x >162\). Quindi il postulato di Bertrand è vero per \(x \ge 162\). D’altra parte si può verificare facilmente che è vero anche per valori inferiori.
6) I numeri primi di Ramanujan
Alla fine del suo articolo Ramanujan dimostra anche il seguente importante teorema:
Teorema 6.1
\[ \lim_{x \to \infty} \pi(2x) – \pi(x) = \infty \]Dimostrazione
In base alle definizioni delle funzioni \(\theta(x)\) e \(\pi(x)\) si ha:
Utilizzando la relazione trovata alla fine della dimostrazione di Ramanujan, troviamo la seguente disuguaglianza:
\[ (\pi(x) – \pi(\frac{x}{2})) > \frac{1}{\ln x}(\frac{x}{6}-3 \sqrt{x}) \text { se \( x > 300\)} \]Da questa facendo dei semplici calcoli possiamo dedurre che:
\[ \pi(x) – \pi (\frac{x}{2}) \ge 1,2,3,4,5, \cdots \text{se \(x \ge 2,11,17,29,41, \cdots\)} \]Definizione 6.1
Per \(n \ge 1\) il numero primo di Ramanujan è definito come il più piccolo intero positivo \(R_{n}\) tale che se \(x \ge R_{n}\) allora:
Notiamo subito che \(R_{n}\) è effettivamente un numero primo, a causa della condizione di minimalità. La funzione di distribuzione \(\pi(x)\) deve aumentare nel punto \(x=R_{n}\). Poiché la funzione \(\pi(x)\) può aumentare ogni volta solo di \(1\), abbiamo anche la seguente relazione:
\[ \pi(R_{n}) – \pi(\frac{R_{n}}{2})=n \]La funzione \(f(x)=\pi(x) – \pi(\frac{x}{2})\) è una funzione a gradini che cresce e diminuisce infinite volte. I salti sono sempre di \(+1\) o \(-1\). Il grafico della funzione ottenuta con il comando (plot PrimePi[2*x] – PrimePi[x] , x from 0 to 50) su WolframAlpha è il seguente:
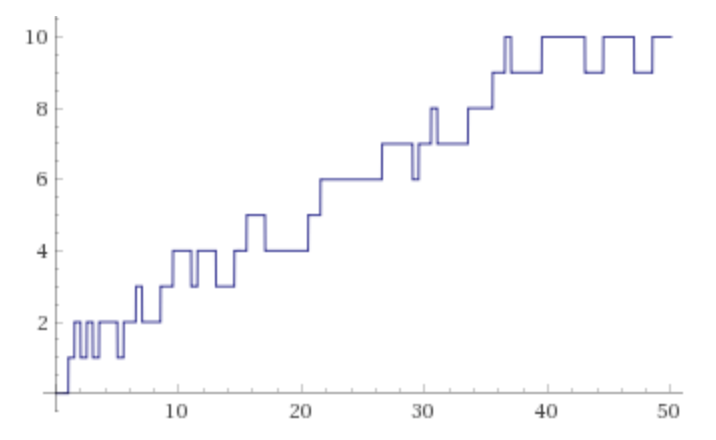
Il postulato di Bertrand equivale a \(R_{1}=2\). Alcuni valori successivi calcolati sono i seguenti:
\[ R_{2}=11; R_{3}=17; R_{4}=29;R_{5}=41 \]I primi di Ramanujan sono stati oggetto di studio di importanti matematici. Ricordiamo in questa sede solo alcune proprietà significative.
Teorema 6.2
Indichiamo con \(p_{n}\) l’ennesimo numero primo nell’ordine crescente. Vale la seguente relazione:
Per una dimostrazione vedere il seguente link.
Teorema 6.3
\[ \lim_{n \to \infty} \frac{R_{n}}{p_{2n}}=1 \]Per una panoramica delle proprietà dei primi di Ramanujan vedere [4] e anche il seguente link.
Conclusione
La dimostrazione del postulato di Bertrand rappresenta un risultato importante nello studio della distribuzione dei numeri primi. In un successivo articolo descriveremo i teoremi di Chebyshev che in seguito porteranno alla dimostrazione del Teorema dei Numeri Primi, effettuata in modo indipendente nel 1896 da parte dei matematici Hadamard e de la Vallée Poussin.
Bibliografia
[1]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers, V edition (Wiley, 1991), pag. 20
[2]M. Aigner, G. Ziegler – Das BUCH der Beweise (Springer)
[3]S. Ramanujan – A proof of Bertrand’s postulate (J. Indian Math. Soc. 11, 1919), 181–182
[4]J. Sondow – Ramanujan primes and Bertrand’s postulate (Amer. Math. Monthly 116, 2009), 630-635
0 commenti