In questo articolo descriveremo il famoso Problema di Basilea, proposto inizialmente dal matematico Pietro Mengoli nel 1644. Descriveremo le prime soluzioni di Eulero e anche soluzioni successive fornite da altri matematici.
1) Il problema di Basilea
Il problema posto da Mengoli consiste nel calcolare la somma della seguente serie infinita
\[ \sum\limits_{n=1}^{\infty}\dfrac{1}{n^{2}} \\ \]La serie è chiaramente convergente e con una piccola calcolatrice si può facilmente calcolare la somma approssimata a \(10\) cifre decimali:
\[ \sum\limits_{n=1}^{\infty}\dfrac{1}{n^{2}} \approx 1,6449340668 \\ \]Il problema venne affrontato dai migliori matematici del tempo, tra i quali in particolare Jacob Bernoulli, Leibniz e Wallis. Si riuscì a calcolare la somma con buona approssimazione; tuttavia il problema rimase irrisolto per diversi anni.
Esercizio 1.1 – Mengoli
\[ \sum\limits_{n=1}^{\infty} \frac{2}{n(n+1)}=2 \\ \]I numeri della forma \( \dfrac{n(n+1)}{2} \) si chiamano numeri triangolari.
Eulero per primo riuscì a risolvere definitivamente il problema posto da Mengoli e scoprì un legame inaspettato con il numero \( \pi \). Il risultato fondamentale dimostrato da Eulero è il seguente:
\[ \sum_{n=1}^{\infty}\frac{1}{n^{2}} = \frac{\pi^{2}}{6} \\ \]Questo legame fra una somma di quadrati di reciproci di numeri interi positivi e una grandezza geometrica fondamentale come \( \pi \) rappresentò una sorpresa per Eulero e per gli altri matematici, e forse è uno dei tanti indicatori della profonda unità di tutta la matematica.
2) Prima pseudo-dimostrazione di Eulero
Per comprendere la prima pseudo-dimostrazione di Eulero, ricordiamo una proprietà dei polinomi.
Teorema 2.1 – Viète
Sia dato il polinomio
Per il Teorema fondamentale dell’algebra esistono \(n\) radici reali o complesse \( \{r_{1},r_{2}, \cdots r_{n}\} \), non necessariamente tutte distinte. Dimostrare che valgono le seguenti formule di Viète:
\[ \begin{array}{l} r_{1}+r_{2}+ \cdots r_{n}=-\frac{a_{n-1}}{a_{n}} \\ \\ r_{1}\cdot r_{2} \cdots r_{n}=(-1)^{n} \frac{ a_{0}}{a_{n}} \\ \end{array} \\ \]Dimostrazione
Basta scrivere \( p(x)=a_{n}(x-r_{1})(x-r_{2}) \cdots (x-r_{n}) \), espandere il prodotto ed uguagliare i coefficienti.
Teorema 2.2
Sia dato un polinomio di grado \( n \) come nel teorema precedente. Allora la somma dei reciproci delle radici è:
Dimostrazione
Sia dato \( p(x)=a_{n}(x-r_{1})(x-r_{2}) \cdots (x-r_{n}) \). Calcolare la derivata prima \( p'(x) \). Facendo il rapporto \( \frac{p'(0)}{p(0)} \) otteniamo subito il risultato voluto.
Un secondo modo di procedere è il seguente: definiamo il polinomio \( q(x)= x^{n}p(\frac{1}{x}) \). Notiamo che \( z \) è uno zero non nullo di \( q(x) \) se e solo se \( \frac{1}{z} \) è uno zero di \(p(x) \). Quindi i reciproci degli zeri di \( p(x) \) coincidono con gli zeri di \( q(x) \), se il termine noto del polinomio \( p(x) \) è non nullo. Da questo ne deriva che la somma dei reciproci delle radici di \( p(x) \) è uguale a \( \frac{-a_{1}}{a_{0}}\).
2.1) Prima dimostrazione di Eulero
Descriviamo ora il metodo euristico di Eulero. Partiamo dallo sviluppo in serie di Taylor della funzione \( \displaystyle\frac{\sin x}{x} \):
\[ \frac{\sin x}{x} =1 – \frac{x^{2}}{3!}+ \frac{x^{4}}{5!}- \cdots + (-1)^{n}\frac{x^{2n}}{(2n+1)!} + \cdots \\ \]Nel punto \( x=0 \) la funzione non ha singolarità in quanto vale il seguente limite notevole:
\[ \lim_{x \to 0} \frac{\sin x}{x}= 1 \\ \]Gli zeri della funzione sono quindi i numeri \( x=\pm \pi, \pm 2\pi, \pm 3\pi, \cdots \). Facciamo la sostituzione \( y=x^{2} \) e scriviamo la seguente equazione:
\[ 1 – \frac{y}{3!}+ \frac{y^{2}}{5!}- \cdots +(-1)^{n}\frac{y^{n}}{(2n+1)!}+ \cdots = 0 \\ \]Gli zeri di questa equazione sono \( y=\pi^{2},4\pi^{2}, \cdots \). A questo punto Eulero suppone che valga il teorema 2.2, come se si trattasse di un polinomio di grado finito e non di una serie infinita. La somma dei reciproci degli zeri dovrebbe essere uguale al coefficiente del termine di primo grado, cambiato di segno:
\[ \frac{1}{\pi^{2}}+ \frac{1}{4\pi^{2}}+ \cdots + \frac{1}{n^{2}\pi^{2}}+ \cdots = \frac{1}{6} \\ \]Da questo deriva la formula finale \( \displaystyle\sum\limits_{n=1}^{\infty}\frac{1}{n^{2}}=\frac{\pi^{2}}{6} \).
Nonostante sia molto brillante, il ragionamento di Eulero non può essere considerato una dimostrazione rigorosa, in quanto si assume valido il teorema 2.2 anche per polinomi di grado infinito. Tuttavia è un esempio del modo di procedere dei matematici: inizialmente si intravede un teorema, pur non avendo ancora una vera dimostrazione. In seguito, se l’intuizione era vera, si riesce poi a dimostrare il teorema.
Ricordiamo comunque che oggi il ragionamento di Eulero può essere reso rigoroso grazie agli sviluppi dell’analisi complessa successivi all’epoca di Eulero, in particolare il teorema di Weierstrass sulla rappresentazioni di funzioni analitiche mediante prodotto infinito costruito sugli zeri della funzione.
2.2) Dimostrazione con il prodotto infinito di \( \displaystyle \boldsymbol{\frac{\sin x}{x}} \)
Un modo sostanzialmente simile al precedente è quello di utilizzare il seguente prodotto infinito dimostrato dallo stesso Eulero (vedi l’articolo su questo sito).
\[ \frac{\sin \pi x}{\pi x} = \prod_{n=1}^{\infty}\left(1- \frac{x^{2}}{n^{2}}\right) \\ \]Considerando lo sviluppo in serie di Taylor della funzione \( \displaystyle\frac{\sin \pi x}{\pi x} \) ed uguagliando i termini di secondo grado a sinistra e a destra della formula di Eulero ritroviamo la formula di Basilea.
3) Seconda dimostrazione di Eulero
In questo caso Eulero utilizza la funzione \( y= \arcsin x \), cioè la funzione inversa della funzione \( x= \sin y \). Questa funzione è definita dell’intervallo \( [-1,1] \) e assume valori nell’intervallo \( [- \frac{\pi}{2},\frac{\pi}{2}] \).
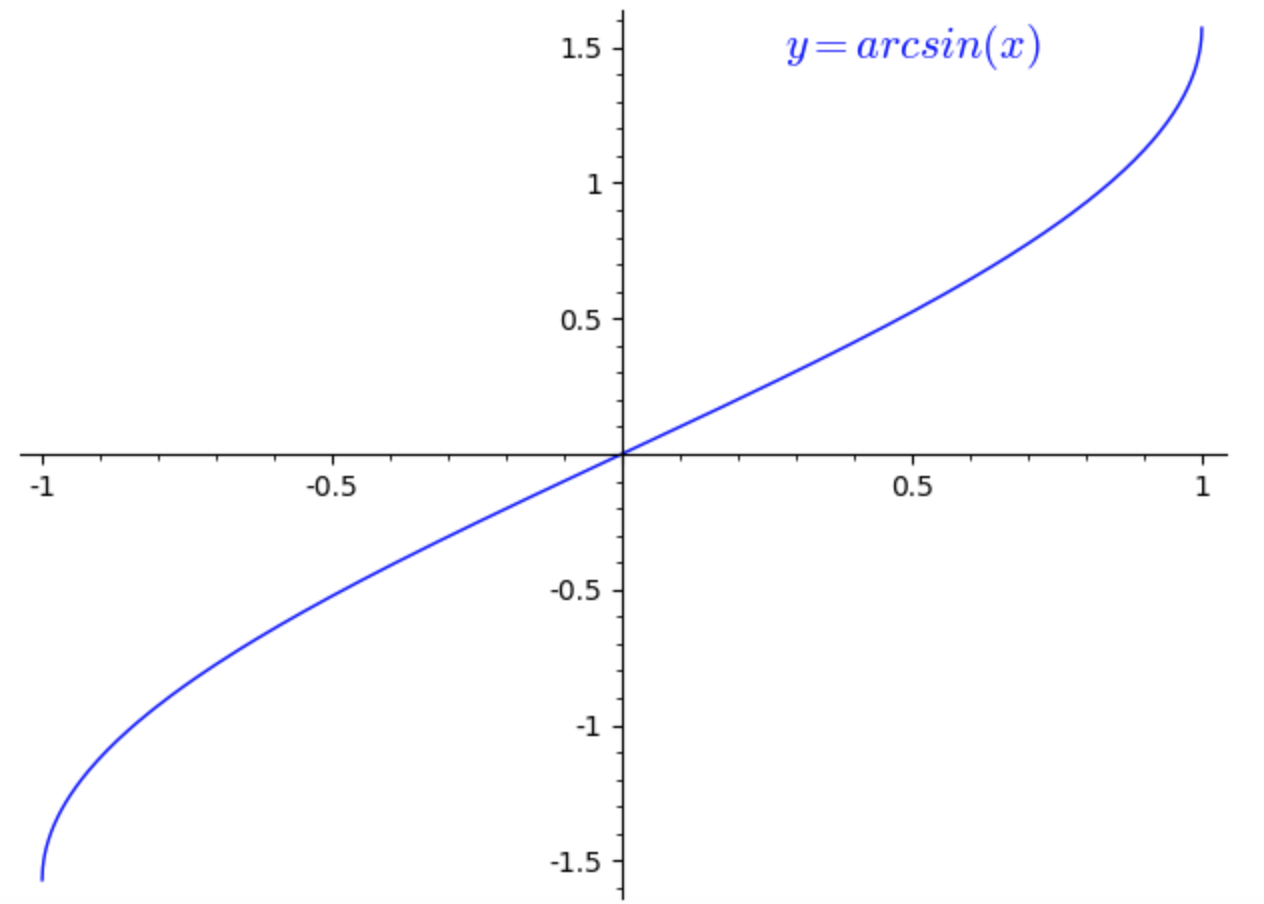
La funzione può essere rappresentata mediante il seguente integrale:
\[ \arcsin x = \int\limits_{0}^{x}\frac{1}{\sqrt{1-t^{2}}} dt \\ \]Calcoliamo la serie binomiale della funzione sotto il segno di integrale e integriamo per serie:
\[ \arcsin x = \int\limits_{0}^{x}\frac{1}{\sqrt{1-t^{2}}} dt= x+ \sum\limits_{k\ge 1}\frac{1 \cdot 3 \cdots (2k-1)}{2 \cdot 4 \cdots \cdot 2k}x^{2k+1} \\ \]Ora consideriamo la seguente formula che può essere ottenuta facilmente mediante integrazione per parti:
\[ \dfrac{1}{2}(\arcsin x)^{2} = \int\limits_{0}^{x}\frac{\arcsin t}{\sqrt{1-t^{2}}} dt \\ \]A questo punto nella funzione integranda sostituiamo la funzione \( \displaystyle\arcsin t \) con lo sviluppo in serie ottenuto in precedenza.
Per completare la dimostrazione Eulero utilizza la formula seguente che può essere ottenuta mediante integrazione per parti:
Mettendo insieme gli ultimi risultati e calcolando la funzione nel punto \( x=1 \), si ottiene la seguente formula, dalla quale deriva subito la formula di Eulero:
\[ \dfrac{\pi ^{2}} {8} = 1 + \frac{1}{3^{2}}+ \frac{1}{5^{2}}+ \cdots + \frac{1}{(2n+1)^{2}}+ \cdots \\ \]Esercizio 3.1
Dimostrare la formula seguente:
Suggerimento
Ricordiamo che l’integrazione per parti consiste nell’utilizzare la seguente formula
Può essere utilizzata sia per gli integrali indefiniti che per gli integrali definiti. Sostanzialmente si devono scegliere le due funzioni \(u,v\) in modo che il calcolo dell’integrale \( \int_{}{}v \cdot du \) sia più facile dell’integrale iniziale \( \int_{}{}u \cdot dv \) . Nel nostro caso conviene porre \( u=t^{n+1},dv=\frac{t}{\sqrt{1-t^{2}}}dt \) e quindi si ottiene facilmente il risultato voluto.
4) Dimostrazione con la serie di Fourier
Calcoliamo lo sviluppo di Fourier della funzione \( f(x)=x, 0 <x <2 \). Possiamo estendere la funzione nell’intervallo \( -2 < x < 2 \) in modo da ottenere una funzione dispari ed estendere la funzione su tutta la retta reale, ottenendo una funzione periodica di periodo uguale a 4.
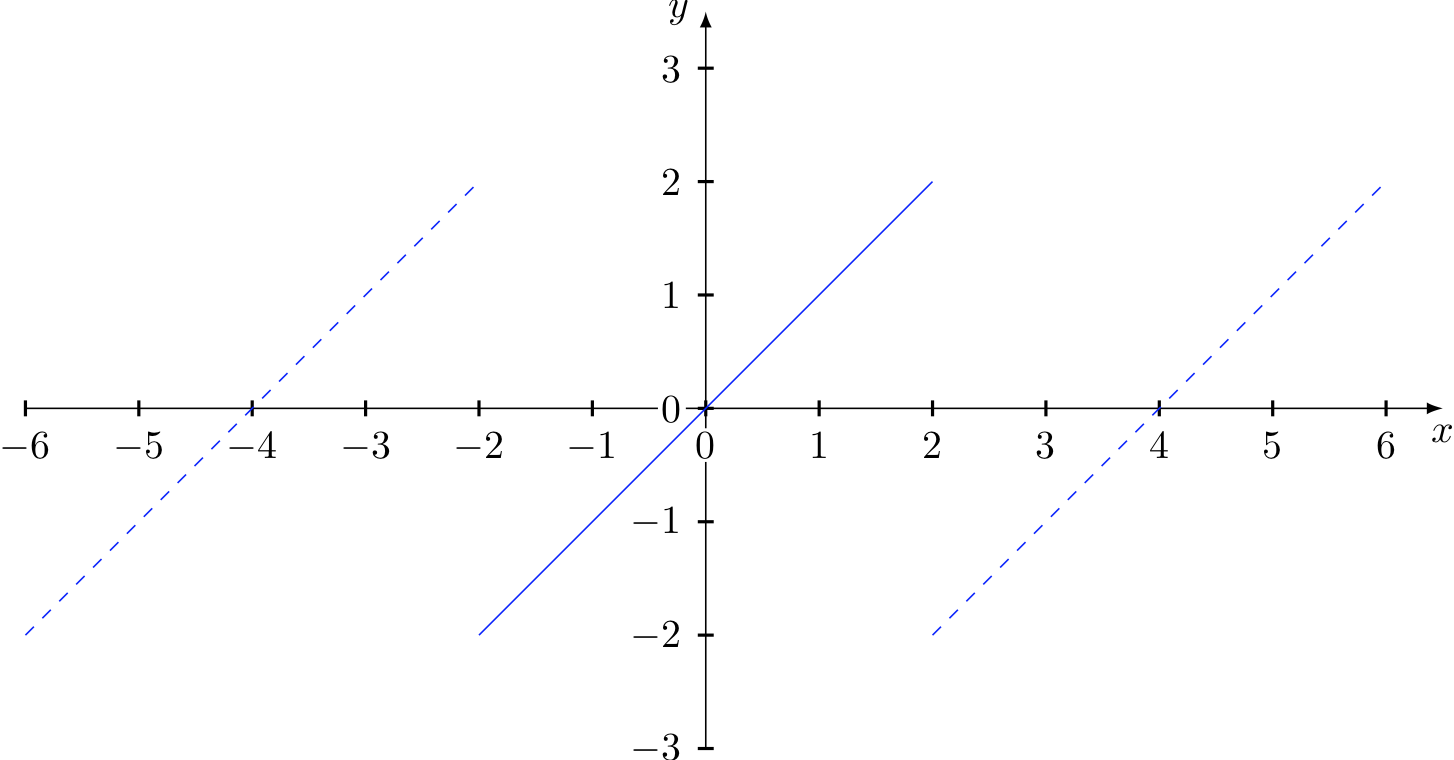
Come è noto le funzioni dispari hanno lo sviluppo di Fourier con solo i termini del seno. Facendo i semplici calcoli si ottiene la seguente serie di Fourier:
\[ f(x)= \dfrac{4}{\pi} \left ( \sin \dfrac{\pi x}{2}- \dfrac{1}{2}\sin \dfrac{2\pi x}{2}+ \dfrac{1}{3}\sin \dfrac{3 \pi x}{2}- \cdots \right) \\ \]Ora integriamo la serie nell’intervallo \( [0,x] \) (si può dimostrare che questo è possibile in quanto la funzione è periodica e continua a tratti). Si ottiene la seguente serie:
\[ x^{2}= K – \dfrac{16}{\pi ^{2}}\left(\cos \dfrac{\pi x}{2}- \dfrac{1}{2^{2}}\cos \dfrac{2\pi x}{2}+ \dfrac{1}{3^{2}}\cos \dfrac{3\pi x}{2}- \cdots \right) \\ \]La costante \(K\) può essere calcolata ponendo \(x=0\). Quindi
\[ K= \dfrac{16}{\pi ^{2}} \left(1 – \dfrac{1}{2^{2}}+ \dfrac{1}{3^{2}} – \cdots \right) \\ \]D’altra parte la costante K corrisponde al termine \(a_{0}\) della serie di Fourier. Quindi abbiamo
\[ K= \dfrac{a_{0}}{2}= \dfrac{1}{2}\int_{0}^{2} x^{2}dx= \dfrac{4}{3} \\ \]Mettendo insieme i due valori per la costante K abbiamo infine la seguente formula:
\[ \sum\limits_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{n^{2}}=\dfrac{\pi^{2}}{12} \\ \]Dalla formula precedente si ricava facilmente la formula di Eulero, sommando separatamente i termini dispari dai termini pari.
Esercizio 4.1
Dimostrare le seguenti formule a partire dalla formula di Basilea:
Per uno studio delle serie e degli integrali di Fourier vedere [1].
5) Altre dimostrazioni
Esistono esistono diverse altre dimostrazioni della formula di Eulero. Alcune utilizzano il calcolo degli integrali di variabili complesse, tramite il Teorema dei residui di Cauchy. Una dimostrazione che utilizza metodi abbastanza elementari è quella fornita dal matematico greco I. Papadimitrou, che si può studiare nell’articolo della rivista The American Mathematical Monthly[2].
Un’altra dimostrazione interessante che utilizza gli integrali doppi si può trovare nella stessa rivista[3].
6) La nascita della funzione zeta
Diamo solo alcuni cenni al legame fra il problema di Basilea e la nascita degli studi sulla funzione zeta di Riemann, una funzione che in seguito avrà un ruolo fondamentale nella Teoria dei numeri, e in altri importanti settori della matematica e della fisica. Viene chiamata funzione zeta di Riemann, ma sarebbe giusto associare anche il nome di Eulero, che per primo ha studiato le sue proprietà. La funzione zeta di Riemann è stata studiata inizialmente da Eulero come funzione di variabile reale, ed è definita in questo modo:
\[ \zeta (s) = \sum_{n=1}^{\infty}\frac{1}{n^{s}} \\ \]dove \( s \) è una variabile reale. La serie converge per ogni valore \( s >1 \). Oltre a calcolare il valore \( \zeta (2) \), Eulero riuscì a calcolare la funzione zeta per altri valori, ad esempio:
\[ \begin{align} \zeta(4) &= \dfrac{\pi ^{4}}{90} \\ \\ \zeta(6) &= \dfrac{\pi ^{6}}{945} \\ \\ \zeta(8) &= \dfrac{\pi ^{8}}{9450} \\ \\ \zeta(10) &= \dfrac{\pi ^{10}}{93555} \end{align} \\ \]In realtà Eulero trovò una formula generale per il calcolo della funzione zeta nei valori pari:
\[ \zeta(2k)=\sum_{n=0}^{\infty}\frac{1}{n^{2k}}=(-1)^{k-1}\frac{B_{2k}}{2(2k)!}(2\pi)^{2k} \\ \]dove \(B_{n}\) sono numeri razionali, chiamati numeri di Bernoulli, definiti dalla seguente funzione generatrice:
\[ \dfrac{x}{e^{x}-1}=1 – \frac{x}{2}+\sum\limits_{n=2}^{\infty}\frac{B_{n}}{n!}x^{n} \\ \]Ricordiamo che numeri \( B_{2n+1}\), con \(n\ge 1 \), sono tutti nulli.
Il calcolo della funzione zeta nei valori interi dispari positivi è risultato molto più difficile e ad oggi non è risolto.
Eulero ha inoltre dimostrato un teorema fondamentale che associa la funzione zeta alla distribuzione dei numeri primi:
In base a questo teorema i valori della funzione zeta sono strettamente correlati con la distribuzione dei numeri primi.
Il contributo fondamentale di Riemann è di avere esteso lo studio della funzione al campo dei numeri complessi. In questo caso si usa la notazione \( s= \sigma + it \), dove \( \sigma,t \) sono variabili reali e \( s \) è una variable complessa. La funzione zeta di Riemann \( \zeta (s) \) nel campo complesso è una delle funzioni più importanti della matematica ed ha un ruolo fondamentale nello studio della distribuzione dei numeri primi.
Esercizio 6.1
Dimostrare la formula di Eulero
Suggerimento
Utilizzare il prodotto infinito
In primo luogo determinare il coefficiente davanti alla potenza \(x^{4}\) nell’espansione in serie di Taylor della funzione a sinistra. Quindi determinare il coefficiente \(K_{4}\) del termine \(x^{4}\) nello sviluppo del prodotto infinito. Questo coefficiente contiene tutti i possibili prodotti dei termini \((-\frac{x^{2}}{n^{2}}), (-\frac{x^{2}}{m^{2}})\) con \( n \neq m\). Quindi il coefficiente è dato dalla doppia somma
\[ K_{4}=\frac{1}{2}\sum\limits_{n=1}^{\infty}\sum\limits_{n \neq m}{}\frac{1}{n^{2}m^{2}} \]Semplificando otteniamo
\[ K_{4}=\frac{1}{2}\left( \sum\limits_{n=1}^{\infty}\frac{1}{n^{2}}\sum\limits_{m=1}^{\infty}\frac{1}{m^{2}} \ – \sum\limits_{n=1}^{\infty}\frac{1}{n^{4}}\right) \]A questo punto abbiamo tutti gli elementi per calcolare il valore di \(\zeta(4)\).
Conclusione
La soluzione del problema di Basilea è di per sé un risultato di una grande bellezza in quanto dimostra il collegamento fra due settori che a prima vista sembrano separati, cioè fra l’aritmetica e la geometria.
Inoltre l’inizio degli studi sulla funzione di Riemann ha portato successivamente a risultati fondamentali nel campo della teoria dei numeri.
Nei prossimi articoli descriveremo le proprietà principali della funzione zeta e il suo legame con la distribuzione dei numeri primi.
Bibliografia
[1]E. Stein, R. Shakarchi – Fourier Analysis: An Introduction (Princeton U.P.)
[2]I. Papadimitriou – A simple proof of the formula \(\sum\limits_{n=1}^{\infty}\frac{1}{n^{2}}=\frac{\pi ^{2}}{6}\) (Amer. Math. Monthly 1973, Volume 80, n.4, pag. 424-425).
[3] D. Ritelli – Another proof of \(\zeta (2)= \frac{\pi ^2}{6} \) (Amer. Math. Monthly 2013, Volume 120, n.7, pag. 642-645).
0 commenti