Esercizi di Matematica Elementare (I)

In questo articolo proponiamo alcuni esercizi di matematica elementare. Per eventuali chiarimenti si può utilizzare la email del blog oppure la sezione commenti.

---

Esercizio 1

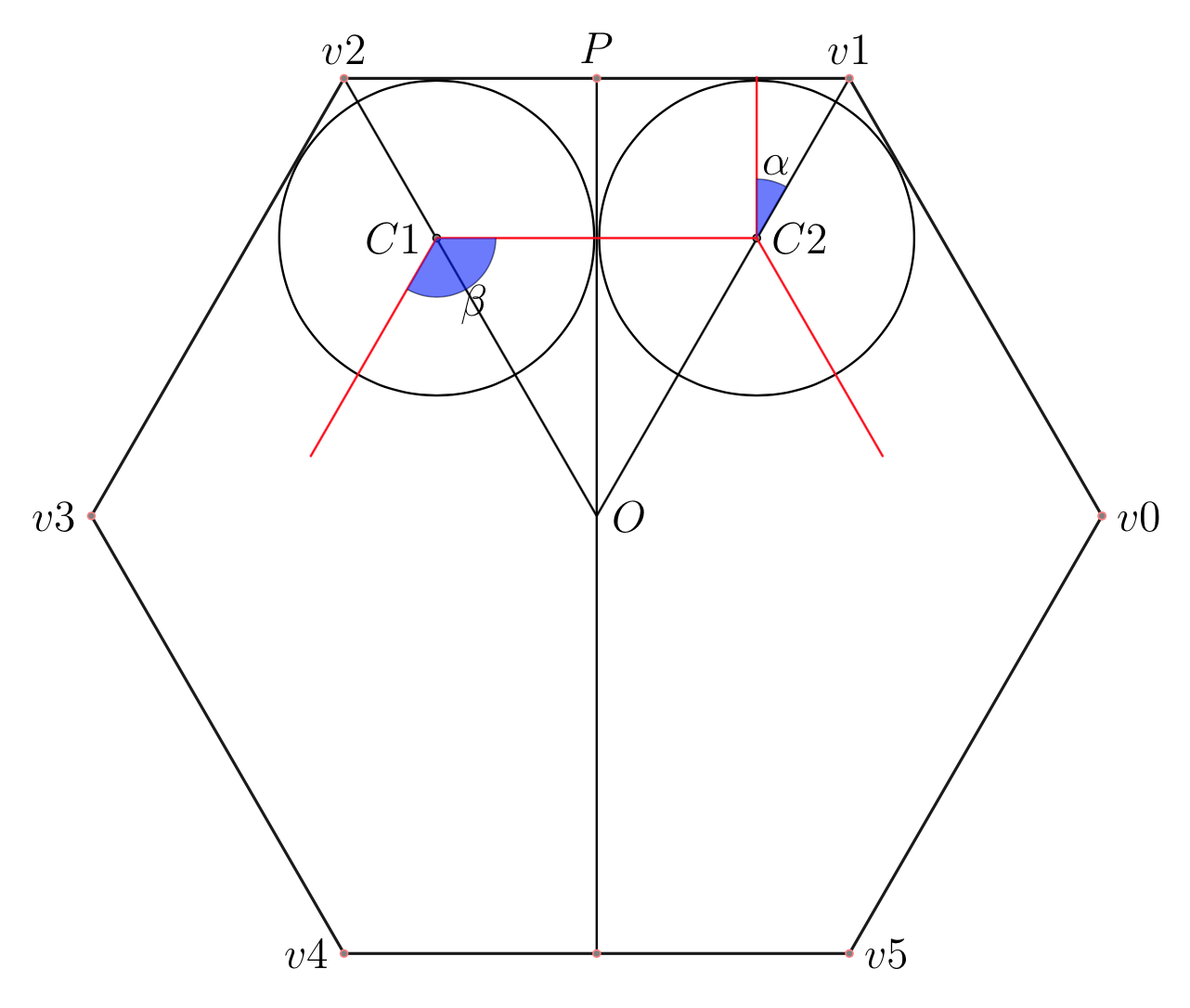
Sia dato un poligono regolare di \(n\) lati, ognuno di lunghezza \(L\), nel quale sono inscritti \(n\) cerchi. Ogni cerchio è tangente a due lati adiacenti del poligono ed a altri due cerchi. Determinare l’area \(A\) della regione stellata formata nel centro del poligono.

Suggerimento
Considerare il poligono simile con i vertici nei centri dei cerchi. I lati del nuovo poligono hanno lunghezza \(2r\) mentre l’area è \((nr^{2}\cot \dfrac{\pi}{n})\). Quindi calcolare l’area della regione interna stellata come differenza fra l’area del poligono interno e la somma delle aree dei settori circolari.

Soluzione

\[ \displaystyle A = \frac{L^{2}}{4}\frac{n \cot \frac{\pi}{n}-(n-2)\frac{\pi}{2}}{(1+\tan \frac{\pi}{n})^{2}} \]

---

Esercizio 2

Dimostrare la seguente relazione:

\[ \sum\limits_{k=1}^{10}\binom{11}{k}2^{k}=3^{11}-2^{11}-1 \\ \]

---

Esercizio 3

Quante diagonali esistono in un poligono convesso di \(n\) lati?

Soluzione

\[ \dfrac{n(n-3)}{2} \]

---

Esercizio 4

Data l’espressione

\[ \left(1+ z + \frac{5}{z}\right)^{6} \]

determinare i termine che non contiene la z.

Suggerimento
Porre \(t= z + \dfrac{5}{z}\) e calcolare lo sviluppo binomiale di \((1+ t)^{6}\). Quindi esaminare lo sviluppo di \(t^{k}\) e individuare i casi nei quali non compaiono le potenze di \(z\).

Soluzione

\[ 1+ \binom{6}{2}\binom{2}{1}\cdot 5 + \binom{6}{4}\binom{4}{2}\cdot 5^{2}+\binom{6}{6}\binom{6}{3}\cdot 5^{3} \\ \]

---

Esercizio 5

Dimostrare la seguente identità di Catalan:

\[ 1-\frac{1}{2}+\frac{1}{3}- \frac{1}{4}+ \cdots + \frac{1}{2n-1}-\frac{1}{2n}=\frac{1}{n+1}+ \frac{1}{n+2}+\cdots + \frac{1}{2n} \\ \]

---

Esercizio 6

Risolvere la seguente equazione:

\[ \frac{\log_{a}(p-x)}{\log_{a}(p+x)}+1 = \frac{2-\log_{p-q}4}{\log_{p-q}(x+q)} \]

dove \( p \gt q \gt 0\).

Soluzioni:

\[ \begin{array}{l} x_{1}= \frac{1}{2}(p-q) + \sqrt{pq} \\ x_{2}= \frac{1}{2}(p-q) – \sqrt{pq} \\ \\ \end{array} \]

---

ESERCIZIO 7

Dimostrare che

\[ \sin\theta \lt \theta \lt \tan\theta \quad \text{se } 0 \lt \theta \lt \frac{\pi}{2} \\ \]

---

Esercizio 8 – Il punto di Lemoine

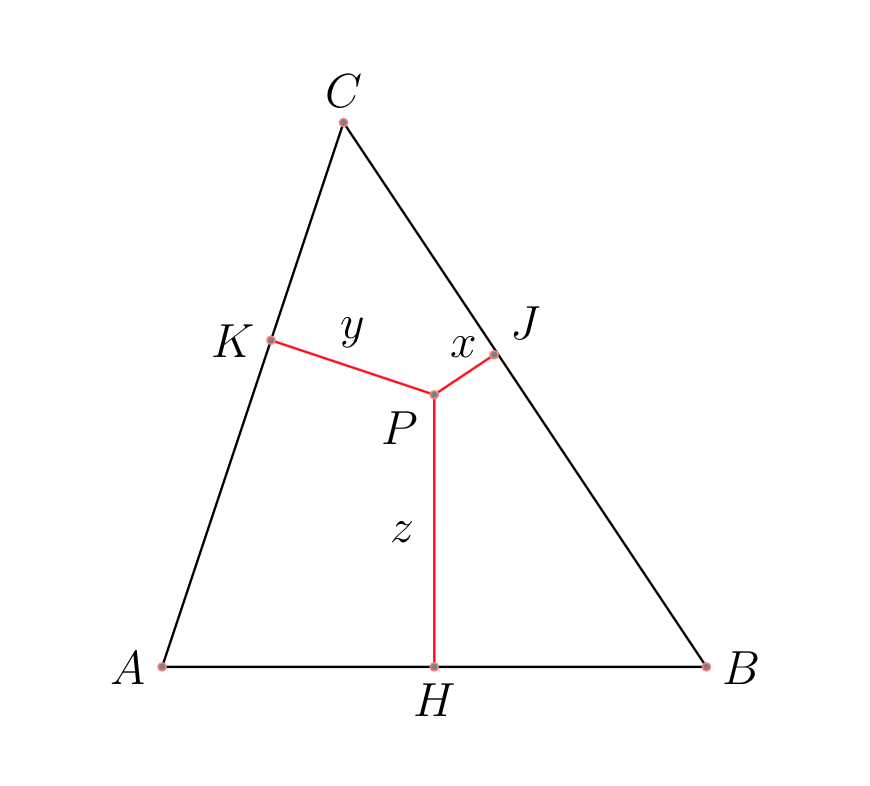
Sia dato un triangolo ABC e un punto interno \(P\). Siano \(x,y,z\) le distanze di \(P\) dai tre lati BC, AC, AB.
Determinare la posizione di \(P\) per la quale la somma \(x^{2}+y^{2}+z^{2}\) assume il valore massimo.

Soluzione
Poniamo \(AB=c,AC=b,BC=a\). La somma \(S=x^{2}+y^{2}+z^{2}\) assume un valore minimo per tutti i punti \(P\) tali che:

\[ \frac{x}{a}= \frac{y}{b}= \frac{z}{c} \]

Si può dimostrare che per ogni triangolo esiste un solo punto con questa proprietà; tale punto si chiama il punto di Lemoine (1840-1912), così chiamato in onore del matematico francese che dimostrò l’esistenza di tale punto.
Geometricamente il punto di Lemoine è definito come il punto di intersezione delle tre simmediane. Le simmediane sono i segmenti che congiungono i vertici del triangolo con i lati opposti e giacciono sulle rette simmetriche delle mediane rispetto alle bisettrici. 
Per dimostrare che il punto di Lemoine è il punto di minimo osserviamo che il minimo della somma \(S\) è lo stesso del minimo della seguente espressione:

\[ \begin{array}{l} Z =(x^{2}+y^{2}+z^{2})(a^{2}+b^{2}+c^{2}) = (ax+by+cz)^{2} \\ + (bx-ay)^{2}+ (cy-bz)^{2}+(cx-az)^{2} \\ \end{array} \]

Ora l’espressione \(ax+by+cz\) è una costante, essendo il doppio dell’area del triangolo. Quindi il minimo di \(Z\) sarà ottenuto quando avremo il minimo della seguente espressione

\[ (bx-ay)^{2}+ (cy-bz)^{2}+(cx-az)^{2} \]

Questa espressione assume il minimo uguale a zero proprio nel punto di Lemoine.

---

Esercizio 9

\[ \begin{array}{l} \displaystyle \sum\limits_{k=1}^{n}\cos(k\alpha) = \dfrac{\sin \dfrac{n\alpha}{2} \cos\dfrac{(n+1)\alpha}{2}}{\sin \dfrac{\alpha}{2}} \quad \alpha \neq 2k\pi\\ \displaystyle \sum\limits_{k=1}^{n}\sin(k\alpha) = \dfrac{\sin \dfrac{(n+1)\alpha}{2} \sin\dfrac{n\alpha}{2}}{\sin \dfrac{\alpha}{2}} \quad \alpha \neq k\pi\\ \end{array} \]

Suggerimento
Alcune formule trigonometriche utili per risolvere gli esercizi sono le seguenti:

\[ \begin{array}{l} \sin \alpha \cos \beta =\frac{1}{2}(\sin(\alpha + \beta) + \sin(\alpha – \beta)) \\ \sin \alpha \sin \beta =\frac{1}{2}(\cos(\alpha – \beta) – \cos(\alpha + \beta)) \\ \cos \alpha \cos \beta =\frac{1}{2}(\cos(\alpha + \beta) + \cos(\alpha – \beta)) \\ \sin \alpha + \sin \beta =2\sin\frac{\alpha + \beta}{2} \cos\frac{\alpha – \beta}{2} \\ \sin \alpha – \sin \beta =2\sin\frac{\alpha – \beta}{2} \cos\frac{\alpha + \beta}{2} \\ \end{array} \]

---

Esercizio 10

Trovare le soluzioni dell’equazione

\[ \sin^{6}x + \cos^{6}x = t \]

dobe \(t\) è un numero reale.

Soluzione

\[ x=\pm \frac{1}{4}\arccos \frac{8t-5}{3}+ \frac{n\pi}{2}, \quad n \in \mathbb{Z} \]

con i valori del parametro \(t\) compresi nell’intervallo \(-1 \le \frac{8t-5}{3}\le 1\) oppure \(\frac{1}{4}\le t \le 1\).

---

Esercizio 11 – Wallis (1616-1703)

Dimostrare la seguente formula:

\[ \displaystyle \lim_{n \to \infty}\frac{0^{k}+1^{k}+2^{k}+ \cdots +n^{k}}{n \cdot n^{k}}=\frac{1}{k+1} \]

dove \(k\) è un intero positivo.

Mediante questo limite calcolare il seguente integrale:

\[ \int_{0}^{1}x^{k}dx = \frac{1}{k+1} \]

dove \(k\) è un intero positivo.

Wallis calcolò l’integrale nel 1655, prima ancora che fosse disponibile il calcolo integrale scoperto da Newton e Leibniz.