Introduzione alla Crittografia e alla Crittoanalisi

La Crittologia è la scienza che si occupa della creazione e della decifrazione dei codici segreti. I codici segreti vengono creati per proteggere e trasmettere in modo sicuro le informazioni. La Crittologia è costituita da due branche fondamentali:

• Crittografia, che si occupa di creare codici segreti per cifrare i messaggi in chiaro;
• Crittoanalisi, che si occupa di decifrare i messaggi cifrati.

La protezione e la trasmissione sicura delle informazioni è una necessità presente in tutte le società umane, fin dall’antichità. Le prime forme di crittografia sono rintracciabili nelle civiltà antiche del medio oriente (Egitto, Grecia, Roma):

• Esempi di testi cifrati sono stati scoperti in alcuni geroglifici dell’antico Egitto, risalenti a circa \(4000\) anni fa. Si tratta di testi scritti su delle tombe che sostanzialmente utilizzavano un semplice metodo di sostituzione dei caratteri del testo originale con altri simboli.
• Intorno al \(500\) a.C gli Spartani utilizzavano la scitala per trasmettere brevi messaggi, soprattutto in tempo di guerra. La scitala era un oggetto cilindrico e il messaggio veniva scritto su una piccola striscia di pelle arrotolata sul cilindro. Se si srotolava la striscia il messaggio era incomprensibile. Per decifrare il testo era necessario arrotolare la striscia su una scitala dello stesso diametro. Il diametro del cilindro era quindi la chiave del cifrario.
• Il codice di Giulio Cesare: si tratta di un semplice cifrario che Cesare utilizzava per comunicare con i suoi ufficiali. Ogni lettera del testo originale viene sostituita con la lettera che si trova ad una distanza fissata nell’ordinamento alfabetico.

La disponibilità dei moderni computer e l’utilizzo di strumenti matematici avanzati hanno permesso di creare sistemi di cifratura molto complessi e difficili da decifrare. D’altra parte la disponibilità dei computer è uno strumento importante anche per l’attività di crittoanalisi, che permette di decifrare sistemi che in precedenza erano inattaccabili.
Nelle società moderne, in cui molte attività fondamentali (economiche, finanziarie, militari, ecc.) si svolgono mediante l’utilizzo di reti di computer sparsi in tutto il mondo e collegati fra loro, la crittografia è diventata una necessità imprescindibile. La crittografia è fondamentale non solo per garantire la riservatezza delle informazioni, ma anche per altri aspetti altrettanto importanti che riguardano la sicurezza delle transazioni online:

• confidenzialità o riservatezza: assicurare che soltanto il destinatario sia in grado di leggere il messaggio;
• autenticazione: determinare se un utente umano o un computer ha i permessi per accedere ad una particolare risorsa;
• integrità: assicurarsi che il messaggio inviato arrivi a destinazione integro nel suo contenuto iniziale, senza essere modificato;
• non-ripudiabilità: chi genera un messaggio non deve in seguito poter negare di averlo inviato. In modo analogo chi riceve un messaggio non deve poter negare di averlo ricevuto. Sono concetti simili alla firma autografa e alla ricevuta di ritorno.

Questo articolo è una introduzione generale alla Crittologia. In articoli successivi approfondiremo i principali sistemi di crittografia e crittoanalisi attualmente in uso. Per una panoramica storica della Crittologia vedere l’importante testo di Khan ^[1].

---

1) I sistemi crittografici

Un sistema crittografico è costituito dai seguenti componenti:

• l’insieme \(M\) dei messaggi in chiaro
• l’insieme \(K\) delle chiavi che è possibile utilizzare nella cifratura
• l’insieme \(C\) dei messaggi cifrati

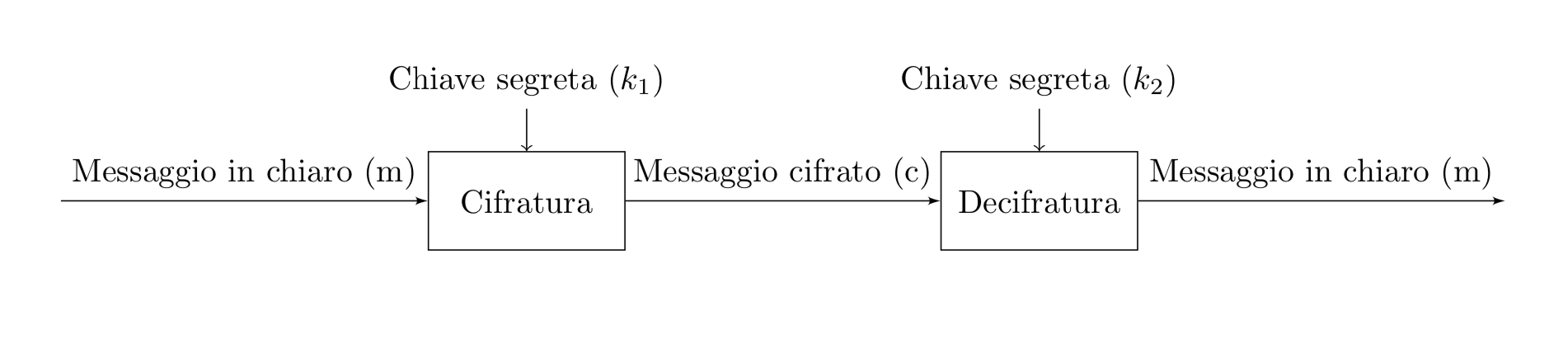
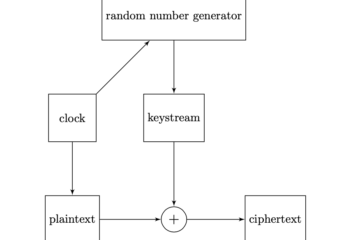
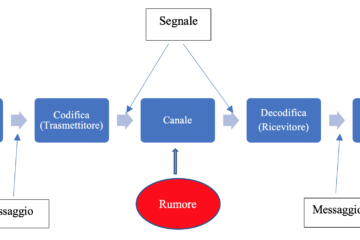
Un messaggio in chiaro \(m\) prodotto da una sorgente \(A\) viene trasformato, mediante un algoritmo di cifratura e una chiave, in un messaggio cifrato \(c\). Il messaggio cifrato viene inviato al destinatario \(B\), il quale mediante un algoritmo di decifratura e una chiave è in grado di ricostruire il messaggio originale. Possiamo rappresentare le operazioni di cifratura e decifratura con i seguenti simboli:

\[ \begin{array}{l} c = C(k_{1},m)\quad \text{ cifratura di } m \text{ con la chiave } k_{1} \\ m= D(k_{2},c)\quad \text{ decifratura di } c \text{ con la chiave } k_{2} \\ \end{array} \]

Il modello fondamentale di un sistema crittografico è illustrato dal seguente diagramma:

L’obiettivo di un buon sistema di cifratura è rendere impossibile, o comunque molto difficile, decifrare il messaggio cifrato senza conoscere la chiave.
Le chiavi di cifratura e decifratura \(k_{1},k_{2}\) possono essere uguali oppure possono essere diverse. Nel primo caso si parla di crittografica simmetrica, mentre nel secondo caso di crittografia asimmetrica.
Come vedremo in seguito esempi di crittografia simmetrica sono gli algoritmi utilizzati dai sistemi DES e AES, mentre l’algoritmo RSA è l’esempio principale di crittografia asimmetrica.

---

2) Confusione e diffusione

Nel \(1949\) C. Shannon, il padre della Teoria dell’Informazione, ha pubblicato un articolo nel quale sono descritte le caratteristiche fondamentali che deve avere un buon sistema di crittografia. L’obiettivo principale è difendersi da attacchi statistici; per questo è importante rendere il più possibile nascoste le proprietà statistiche del messaggio originale, e quindi rendere difficile trovare la chiave. Shannon ha individuato due proprietà fondamentali:

• Confusione
• Diffusione

L’obiettivo della confusione è di rendere molto complessa la relazione fra il testo cifrato e il valore della chiave. La chiave deve essere il più possibile scollegata dal testo cifrato, in modo da rendere difficile effettuare analisi statistiche. Ogni cifra binaria (bit) del testo cifrato dovrebbe dipendere da varie parti della chiave, oscurando quindi le connessioni fra loro. Come vedremo la confusione può essere ottenuta mediante algoritmi complessi di sostituzione e rimescolamenti dei caratteri del testo in chiaro.
L’obiettivo della diffusione è di rendere molto complessa la relazione fra il testo in chiaro e il testo cifrato, in modo da rendere impossibile decifrare il testo mediante un’analisi statistica. Ogni carattere del testo in chiaro dovrebbe influenzare diversi caratteri del testo cifrato e viceversa.
Nel caso ottimale, se cambiamo un singolo bit del testo in chiaro, allora mediamente dovrebbero cambiare la metà dei bit del testo cifrato, e viceversa.

---

3) Gli interi e i numeri primi

La Teoria dei Numeri studia gli interi e le loro proprietà: divisibilità, numeri primi, fattorizzazione, ecc. Nonostante in apparenza si tratti di una disciplina teorica, nel corso degli ultimi anni la Teoria dei Numeri ha assunto un ruolo importante in diversi settori della scienza e della tecnologia, e in particolare nello studio degli algoritmi della moderna Crittografia. In questa sede facciamo un breve riepilogo delle proprietà elementari; in articoli successivi studieremo argomenti più avanzati.

3.1) Divisibilità degli interi

L’insieme degli interi  \(\mathbb{Z}\) è ottenuto dai naturali aggiungendo i numeri negativi: 

\[ \mathbb{Z}=\{…,-4,-3,-2,-1,0,1,2,3,4,…\} \]

Si dice che un intero \(b\) è divisibile da un intero \(a \neq 0\) se risulta \(b=ax\), dove \(x\) è un intero. Si usa la notazione \(a |b\). Si assume che per ogni intero non nullo \(a\) risulti \(a | 0\) in quanto \(a\cdot 0 = 0\). Dati due interi \(a,b\), si chiama divisore comune un intero \(x\) che divide entrambi. Il massimo comune divisore di due interi non nulli di \(a,b\) è il più grande intero positivo che divide entrambi. Viene indicato con \(MCD(a,b)\) oppure semplicemente con \((a,b)\).
Il minimo comune multiplo di due interi \(a,b\) è il più piccolo intero positivo che è un multiplo di entrambi. Viene indicato con \(MCM(a,b)\) oppure con \( [a,b]\).

Esempio 3.1

\[ \begin{array}{l} (99,30)=3 \\ (25,3)= 1 \\ [10,31]=310 \\ [27,6]=54 \end{array} \]

Esercizio 3.1
Dimostrare che se \(a | b\) e \(a | c\) allora \(a |(bx+cy)\) per tutti gli \(x,y \in \mathbb{Z}\).

Esercizio 3.2
Dimostrare che se \(a | b\) e \(b | a\) allora \(a = \pm b\) .

Teorema 3.1 – Teorema di divisione di Euclide
Dato un intero \( k > 0\)  e un intero  \(n\), esistono due unici interi \(q,r\) tali che: 

\[ n = kq+ r \quad 0 \le r \lt k \]

Dimostrazione
Per dimostrare il teorema utilizzeremo il principio del buon ordinamento. Dimostriamo prima l’esistenza. Consideriamo l’insieme

\[ S = \{n- xk | x \in \mathbb{Z}, n-xk\ge 0\} \]

Si tratta di un insieme di interi non vuoto e limitato inferiormente, e quindi esiste un elemento minimo, indicato con \(r=n-kq\), che appartiene all’insieme. Il numero \(r\) verifica le seguenti disuguaglianze

\[ 0 \le r = n-kq \lt k \]

Vediamo ora l’unicità. Supponiamo per assurdo che esistano due rappresentazioni diverse \(n=kq+r=kq_{1}+r_{1}\). Ne deriva \( r-r_{1}=k(q_{1}-q)\). Da questo ne consegue

\[ k > |r-r_{1}| = |q-q_{1}|k \ge k \]

che implica \(q=q_{1},r=r_{1}\).

Teorema 3.2 – Algoritmo di Euclide
Dati due interi \(a,b\), non entrambi nulli, il massimo comune divisore \((a,b)\) esiste ed è unico.

Dimostrazione
L’esistenza viene dimostrata mediante l’algoritmo di Euclide, il quale permette anche di calcolare il massimo comune divisore di due interi. L’algoritmo si basa sull’osservazione che un divisore comune di due interi deve dividere anche la loro differenza. Dati due interi \(a,b\) con \(b > 0\) l’algoritmo di Euclide effettua un numero finito di divisioni secondo lo schema seguente: 

\[ \begin{array}{l} a = b q_{1}+ r_{1}, \quad 0 \lt r_{1} \lt b \\ b= r_{1}q_{2} + r_{2} \quad 0 \lt r_{2} \lt r_{1} \\ r_{1}= r_{2}q_{3} + r_{3} \quad 0 \lt r_{3} \lt r_{2} \\ \vdots \\ r_{n-2}= r_{n-1}q_{n} + r_{n} \quad 0 \lt r_{n} \lt r_{n-1} \\ r_{n-1}=r_{n}q_{n+1} \end{array} \]

L’algoritmo termina dopo un numero finito di passi poiché

\[ b \gt r_{1} \gt r_{2} \gt \cdots \]

Il massimo comune divisore \( (a,b)\) di \(a\) e \(b\) è  \( r_{n}\), l’ultimo resto non nullo nell’algoritmo di Euclide. Infatti, proseguendo all’indietro si verifica che \(r_{n}\) divide gli altri resti \(r_{n-1},r_{n-2}, \cdots ,r_{1}\) e quindi divide anche \(a\) e \(b\). Inoltre, se un altro intero \(d\) divide \(a\) e \(b\), allora procedendo dall’inizio si vede che divide tutti i resti fino a \(r_{n}\). L’algoritmo di Euclide quindi dimostra l’esistenza del MCD. D’altra parte è facile verificare anche che il MCD deve essere unico.

Teorema 3.3 – Bezout
Se \( (a,b)=d\), allora esistono due interi \( x,y \in \mathbb{Z}\) tali che

\[ ax + by = d \]

Per dimostrare il teorema di Bezout basta partire dall’algoritmo di Euclide. Prendere l’ultimo resto non nullo \(r_{n}\) e proseguire all’indietro, esprimendo \(r_{n}\) come combinazione lineare dei numeri iniziali \(a,b\).
È facile verificare che gli interi \(x,y\) non sono unici.

3.2) I numeri primi

Ogni intero è divisibile per se stesso e per il numero \(1\). Un intero positivo \(n >1\) si dice primo se non ha altri divisori, oltre quelli banali, altrimenti di dice composto. Il numero \(1\) non viene considerato primo. Negli ‘Elementi’ di Euclide viene data la dimostrazione che esistono infiniti numeri primi. Nel Libro VII degli Elementi, nella proposizione \(30\), viene enunciato quello che oggi è conosciuto come il lemma di Euclide, che in forma moderna è il seguente: 

Teorema 3.4 – Lemma di Euclide
Dato un numero primo \(p\) e due interi \(a,b\), se \(p\) divide il prodotto \(ab\), allora \(p\) divide \(a\) oppure \(p\) divide \(b\). In simboli

\[ p | ab \implies p|a \lor p|b \]

dove \(\lor\) è il simbolo logico usato per indicare “oppure”.

I numeri primi sono considerati i mattoni della matematica. Questo è dovuto al teorema fondamentale dell’aritmetica:

Teorema 3.5 – Teorema fondamentale dell’aritmetica
Ogni numero naturale \(n > 1\) può essere rappresentato in modo univoco come prodotto finito di potenze di primi distinti:

\[ n= p_{1}^{a_{1}}p_{2}^{a_{2}} \cdots p_{k}^{a_{k}} =\prod\limits_{i=1}^{k}p_{i}^{a_{i}} \]

La decomposizione è unica, a parte l’ordine dei fattori. La dimostrazione segue facilmente dal lemma di Euclide.

---

4) L’Aritmetica Modulare di Gauss

Dato un intero positivo \(m\), si dice che due interi \(a\) e \(b\) sono congruenti modulo \(m\) se danno lo stesso resto nella divisione per \(m\). Si usa la seguente notazione introdotta dal matematico tedesco Gauss:

\[ a \equiv b \pmod{m} \]

Ad esempio \(23 \equiv 2 \pmod {3}\) , \(1000 \equiv 1 \pmod {3}\).
Dal teorema di divisione di Euclide segue che, se \(m\) è un intero non negativo, allora per ogni intero \(a\) esiste un unico intero non negativo \(r\) tale che

\[ a \equiv r \pmod {m} \quad 0 \le r \lt m \]

Si può dimostrare facilmente che la relazione di congruenza è una relazione di equivalenza (riflessiva, simmetrica e transitiva) e quindi induce una partizione dell’insieme degli interi \(\mathbb{Z}\) in \(m\) classi di equivalenza disgiunte, che cioè non hanno elementi in comune. Ogni classe di equivalenza contiene tutti interi congruenti fra loro, cioè che danno lo stesso resto nella divisione per \(m\).
Un sistema completo di residui \(\pmod {m}\) è un insieme di \(m\) numeri distinti, ognuno preso da una delle \(m\) classi di equivalenza.
La rappresentazione standard per le classi della congruenza modulo \(m\) è formata prendendo come rappresentanti gli elementi dell’insieme \(\{0,1,2,\cdots,m-1\}\).
Ad esempio se \(m=3\) abbiamo \(3\) classi di equivalenza indicate con il simbolo \(\overline{n}\):
\(\overline{0} \) : contiene gli interi \({-6,-3,0,3,6,9,..}\)
\(\overline{1}\) : contiene gli interi \({-8,-5,-2,1,4,7,10,..}\)
\(\overline{2}\) : contiene gli interi \({-7,-4,-1,2,5,8,11,..}\)

Esercizio 4.1
Dimostrare che se \(a \equiv b \pmod{m}\) e \(c \equiv d \pmod{m}\) allora

\[ \begin{array}{l} (a+c) \equiv (b +d) \pmod{m} \\ ac \equiv bd \pmod{m} \end{array} \]

In base all’esercizio precedente possiamo definire le operazioni di addizione e moltiplicazione sulle classi residuo:

\[ \begin{array}{l} \overline{a} + \overline{b} = \overline{a+b} \\ \overline{a} \cdot \overline{b} = \overline{ab} \end{array} \]

Le operazioni sono ben definite e non dipendono dai particolari rappresentanti delle classi. L’insieme degli interi modulo \(m\) con le operazioni di somma e prodotto viene indicato con il simbolo \(\mathbb{Z}/m\mathbb{Z}\).

Esempio 4.1
Nell’insieme \(\mathbb{Z}/4\mathbb{Z}\) verificare le seguenti operazioni tra le classi

\[ \begin{array}{l} \overline{1} + \overline{3}=\overline{0} \\ \overline{2} + \overline{3}=\overline{1} \\ \overline{2} + \overline{2}=\overline{0} \\ \overline{3} + \overline{3}=\overline{2} \\ \end{array} \]

Teorema 4.1
Se \((k,m)=1\) allora

\[ ka \equiv kb \pmod{m} \implies a \equiv b \pmod {m} \]

Dimostrazione
Dalle ipotesi abbiamo

\[ k(a-b) = tm \quad t \in \mathbb{Z} \]

Poiché \(m\) non divide \(k\) deve essere \(m|(a-b)\), cioè \(a \equiv b \pmod{m}\).

4.1) Le equazioni congruenziali

Un settore importante della Teoria dei Numeri è lo studio delle equazioni alle congruenze, cioè equazioni del tipo \(f(x) \equiv 0 \pmod{m}\), dove \(f(x)\) è un polinomio a coefficienti interi. Le soluzioni vengono considerate distinte solo se appartengono a classi di equivalenza diverse.
Il caso più semplice è costituito dalle equazioni congruenziali lineari, cioè equazioni del tipo

\[ ax \equiv b \pmod{m} \]

dove \(a,b \in \mathbb{Z}\). Questa equazione alle congruenze è equivalente alla equazione aritmetica \(ax-my=b\), con \(m\) intero, che è risolubile in interi se e solo se \(d=(a,m)|b\). Questa proprietà è espressa nel seguente:

Teorema 4.2
Se \((a,m)=d\), allora l’equazione \(ax \equiv b \pmod{m}\) ammette soluzioni se e solo se \(d|b\).

Per quanto riguarda il numero delle soluzioni, vale il seguente:

Teorema 4.3
L’equazione lineare \(ax \equiv b \pmod {m}\), se \(d=(a,m)|b\), ha esattamente \(d\) soluzioni diverse \(\pmod{m}\).
Infatti se \(x_{0}\) è una soluzione, lo sono anche le seguenti

\[ \{x_{0} + \frac{m}{d},x_{0} + \frac{2m}{d},\cdots ,x_{0} + \frac{(d-1)m}{d}\} \]

In particolare, la soluzione è unica se \(d=(a, m)=1\).
Si definisce l’inverso di a \(\pmod {m}\) un intero b tale che \( a · b \equiv 1 \pmod {m}\). Si usa la notazione \(a^{-1}\) per indicare l’inverso di a \(\pmod {m}\).

Dal teorema precedente segue che un inverso di a \(\pmod {m}\) esiste se e solo se \((a,m)=1\).

Esempio 4.2
Consideriamo l’equazione \(3x \equiv 18 \pmod {21}\).
Abbiamo \(d=(3,21)=3\) e \(3|18\). Quindi esistono \(3\) soluzioni distinte.
Una soluzione che si può facilmente trovare è \(x_{0}=6\). Le altre due sono \(x_{1}= 6 + \dfrac{21}{3}=13\) e \(x_{2}= 6 + \dfrac {2 \cdot 21}{3}=20\).

Ricordiamo infine, senza dimostrazione, il seguente teorema che è molto utile:

Teorema 4.4 – Teorema cinese del resto
Siano \(m_{1},m_{2},\cdots,m_{k}\) interi positivi relativamente primi fra loro, e siano \(a_{1},a_{2},\cdots,a_{k}\) degli interi arbitrari. Allora esiste un intero \(x\) tale che

\[ \begin{array}{l} x \equiv a_{1} \pmod{m_{1}} \\ x \equiv a_{2} \pmod{m_{2}} \\ \vdots \\ x \equiv a_{k} \pmod{m_{k}} \\ \end{array} \]

Inoltre un altro intero \(y\) è soluzione del sistema di congruenze se e solo se

\[ x \equiv y \pmod{m} \quad \text{ dove } m=\prod\limits_{i=1}^{k}m_{i} \]

Per risolvere il sistema lineare di congruenze utilizzare il seguente algoritmo:

• per ogni \(i=1,2,\cdots,k\) calcolare \(z_{i}=\dfrac{m}{m_{i}}\);
• per ogni \(i=1,2,\cdots,k\) calcolare \(y_{i}=z_{i}^{-1} \pmod{m_{i}}\). Questo è possibile poiché \((z_{i},m_{i})=1\);
• la soluzione del sistema è \(x=a_{1}y_{1}z_{1}+ \cdots +a_{k}y_{k}z_{k}\).

Esercizio 4.2
Risolvere il seguente sistema di congruenze

\[ \begin{array}{l} x \equiv 2 \pmod{3} \\ x \equiv 2 \pmod{7} \\ \vdots \\ x \equiv 3 \pmod{5} \\ \end{array} \]

Soluzione: \(x \equiv 23 \pmod{105}\)

---

5) Richiami di Algebra: gruppi, anelli e campi

Ricordiamo brevemente alcuni concetti relativi alle strutture algebriche.

5.1) Gruppi

Un gruppo consiste in un insieme \(G\) sul quale è definita una operazione binaria che ad ogni coppia di elementi di \(G\) associa un elemento sempre dell’insieme \(G\), che indichiamo con \(a \cdot b\):

\[ (a,b) \to a \cdot b \]

tale che siano soddisfatte le seguenti proprietà:

• \(a,b \in G \implies a\cdot b \in G\).
• \(a,b,c \in G \implies a\cdot (b \cdot c) = (a \cdot b) \cdot c\).
• Esiste un \(e \in G\) tale che \(a \cdot e = e \cdot a = a \quad \forall a \in G\). L’elemento \(e\) si chiama elemento identità o elemento neutro.
• Per ogni \(a \in G \) esiste un \(b \in G\) tale che \(a\cdot b = b \cdot a = e\). L’elemento \(b\) viene chiamato l’inverso di \(a\) e denotato con \(a^{-1}\).

Un gruppo di dice commutativo o abeliano se

\[ a \cdot b=b \cdot a \quad \forall a,b\in G \]

L’operazione binaria può essere indicata con qualsiasi simbolo. In genere si utilizza il simbolo \(\cdot\). Per i gruppi additivi si utilizza il simbolo \(+\).
L’ordine di un gruppo è il numero degli elementi del gruppo. Può essere finito o infinito.
Un sottoinsieme H di G si dice sottogruppo se soddisfa tutte le proprietà di cui sopra con la stessa operazione binaria. Per i gruppi finiti vale il seguente importante teorema di Lagrange:

Teorema 5.1 – Lagrange
L’ordine di un sottogruppo di un gruppo finito \(G\) è un divisore dell’ordine di \(G\).

Esempio 5.1
L’insieme degli interi \(\mathbb{Z}\) è un gruppo rispetto alla operazione di addizione. L’inverso di un elemento \(a\) è l’opposto \(-a\). L’elemento neutro rispetto alla operazione di gruppo è lo zero.
Naturalemente l’insieme \(\mathbb{Z}\) non è un gruppo rispetto alla operazione di moltiplicazione. Solo i numeri \(\pm 1\) hanno un inverso moltiplicativo.
L’insieme dei numeri razionali \(\mathbb{Q}\) è un gruppo rispetto alla operazione di addizione.
L’insieme dei numeri razionali \(\mathbb{Q}\) non nulli è un gruppo rispetto alla operazione di moltiplicazione. L’inverso di un numero razionale non nullo \(\dfrac{a}{b},\ a,b \neq 0\), è \(\dfrac{b}{a}\).

Esempio 5.2 – Il gruppo simmetrico
Indichiamo con \(S_{n}\) l’insieme di tutte le permutazioni sull’insieme \(X = \{1,2,…,n\}\). Come operazione binaria utilizziamo la composizione di due permutazioni. È facile verificare che \(S_{n}\) è un gruppo con questa operazione. L’ordine di \(S_{n}\) è \(n!\), cioè il numero totale delle permutazioni.
Ad esempio

\[ S_{3} = \{123, 132, 213, 231, 312, 321\} \]

Data una permutazione \(\sigma \in S_{n},\ i \in \mathbb{N}\), definiamo la permutazione \(\sigma ^i \ge 0\), ottenuta componendo la \(\sigma\) con se stessa \(i\) volte. Allora l’insieme \(\{\sigma ^i| i\ge 0\}\) è il sottogruppo generato dalla permutazione \(\sigma\) e viene indicato con \(\langle \sigma \rangle\).

Esempio 5.3
È facile verificare che l’insieme delle classi residuo \(\mathbb{Z}/m\mathbb{Z}\) è un gruppo commutativo rispetto alla operazione di addizione di classi. L’elemento neutro è la classe \(\overline{0}\).

Esempio 5.4
L’insieme delle classi residuo \(\mathbb{Z}/m\mathbb{Z}\) in genere non è un gruppo rispetto alla operazione di moltiplicazione.
Ad esempio se \(m=6\) non esiste l’inversa moltiplicativa della classe \(\overline{2}\). In altri termini la congruenza

\[ 2x \equiv 1 \pmod{6} \]

non ha soluzione. Il problema è che il numero \(2\) non è primo con il modulo.
Vale infatti il seguente teorema:

Teorema 5.2
Supposto \(m >0\), una classe residuo \(\overline{a} \in \mathbb{Z}/m\mathbb{Z}\) ha un inverso moltiplicativo, cioè esiste una classe \(\overline{x}\) tale che

\[ \overline{a}\cdot \overline{x}=\overline{1} \]

se e solo se \((a,m)=1\).

Dimostrazione
Supponiamo che \((a,m)=1\). Allora per l’identità di Bezout sappiamo che esistono interi \(x,y\) tali che \(ax+my=1\), ma questo equivale alla congruenza \(ax \equiv 1 \pmod{m}\), e quindi alla \(\overline{a}\cdot\overline{x}=\overline{1} \).
Viceversa supponiamo che esista l’elemento inverso \(\overline{x}\). La congruenza \(ax \equiv 1 \pmod {m}\) equivale all’equazione \(ax+my = 1\) con \(y \in \mathbb{Z}\). Questa equazione implica che qualunque divisore di \(a,m\) deve dividere il numero \(1\) e quindi \(a,m\) sono primi fra loro.

Gruppi ciclici
Dato un elemento \(a\) di un gruppo \(G\) e un intero \(n\) possiamo definire le potenze:

\[ \begin{array}{l} a^{n}= a \cdot a \cdots a \\ a^{0}=1 \\ a^{-n}=(a^{-1})^{n}= a^{-1}\cdot a^{-1} \cdots a^{1} \end{array} \]

Teorema 5.3
Per ogni \(a \in G\) e \(n,m \in \mathbb{Z}\) si ha

\[ a^{n} \cdot a^{m}=a^{n+m}; \quad (a^{n})^{m}=a^{nm} \]

Si chiamo ordine di un elemento \(a \in G\) il più piccolo intero positivo, se esiste, tale che \(a^{n}=1\).
Nel caso di gruppi additivi si usa la notazione \(na=0\).

Un gruppo \(G\) si dice ciclico se esiste un elemento \(g \in G\) tale che, per ogni elemento \(h \in G\) si ha \(h = g^{n}\), per qualche intero \(n\). L’elemento \(h\) si chiama generatore del gruppo.
Tutti i gruppi ciclici sono commutativi (o abeliani), in quanto le operazioni di potenze hanno questa proprietà.

Esempio 5.5
Il gruppo additivo degli interi \(\mathbb{Z}\) è ciclico. I suoi generatori sono \(\pm 1\).

Esercizio 5.1
Dimostrare che il gruppo additivo \(\mathbb{Z}/m\mathbb{Z}\) è ciclico per ogni valore di \(m\).

5.2) Anelli

Sia \(R\) un insieme non vuoto nel quale sono definite due operazioni binarie chiuse, che chiamiamo addizione e moltiplicazione e indichiamo con i simboli \(+,\cdot\). La struttura \((R;+,\cdot)\) è un anello se sono verificate le seguenti proprietà per tutti gli \(a,b,c \in \mathbb{R}\):

• \((R;+) \quad \text{è un gruppo abeliano con l’operazione di addizione}\);
• \(a \cdot (b \cdot c) = (a \cdot b) \cdot c  \quad \quad \textbf{proprietà associativa}\);
• \(a \cdot (b + c) = a \cdot b+ a \cdot c \quad \textbf{proprietà distributiva}\);
• \((a+b)\cdot c = a \cdot c+ b \cdot c  \quad \textbf{proprietà distributiva}\).

Un anello (R) si dice commutativo se risulta \(a \cdot b=b \cdot a\) per tutti gli elementi \(a,b \in R\).
Un anello si chiama unitario o anello con unità se esiste un elemento neutro rispetto alla moltiplicazione. Tale elemento si indica con il simbolo \(1\). Per un anello con unità abbiamo quindi:

\[     a \cdot 1 = 1 \cdot a \quad \forall a \in R \]

Se non specificato diversamente, con il termine anello intenderemo anello unitario.
Un anello commutativo si chiama dominio di integrità se non ha divisori dello zero, cioè se il prodotto di due elementi non nulli è non nullo. In termini equivalenti se vale la legge di cancellazione del prodotto:

\[     a \cdot b = 0  \implies (a=0) \lor (b=0) \quad \forall a,b \in R \]

Dato un anello \(R\), un sottoinsieme \(S \subset R\) è un sottoanello se \(S\) verifica gli assiomi dell’anello con le stesse operazioni binarie.

Esempio 5.6
L’insieme degli interi \(\mathbb{Z}\) con le operazioni di addizione e moltiplicazione è l’esempio più importante di anello commutativo unitario. Naturalmente è anche un dominio di integrità, non avendo divisori dello zero.

Esempio 5.7
L’insieme delle classi residuo \(\mathbb{Z}/m\mathbb{Z}\) è un anello commutativo con unità. L’unità moltiplicativa è la classe \(\overline{1}\). Questo anello si chiama anello delle classi residuo modulo \(m\).
Non è tuttavia un dominio di integrità, in quanto in genere non vale la legge di cancellazione. Ad esempio

\[ 1 \cdot 2 \equiv 2 \cdot 4 \pmod{6}, \]

tuttavia non possiamo cancellare il fattore comune, in quanto \(1 \not \equiv 4 \pmod{6}\).
Vale il seguente teorema:

Teorema 5.4
L’anello \(\mathbb{Z}/m\mathbb{Z}\) è un dominio di integrità se e solo se \(m\) è un numero primo.

Dato un anello \(R\) si chiama caratteristica dell’anello, e si indica con \(\text{char}(R)\), il più piccolo intero positivo \(n\) tale che \(na =0\), per ogni \(a \in R\). Se tale \(n\) non esiste, si dice che l’anello ha caratteristica uguale a zero.
Chiaramente \(\text{char}(\mathbb{Z})=0\), mentre \(\text{char}(\mathbb{Z}/m\mathbb{Z})=m\).

Esercizio 5.2
Dimostrare che se \(R\) è un dominio di integrità con caratteristica positiva, allora \(\text{char}(R)=p\), dove \(p\) è un numero primo.

5.3) Campi

Un campo è un anello commutativo unitario \(\mathbb{F}\) tale che per ogni \( a \in \mathbb{F}\), con \(a \ne 0\), esiste un elemento \(a^{-1} \in \mathbb{F}\) tale che \(aa^{-1}=1\).
Un campo è anche un dominio di integrità, in quanto vale la legge di cancellazione. Infatti se \(ac=bc\) allora

\[ a = a1 = a (c c^{-1}) = (ac)c^{-1} = (bc)(c^{-1}) = b(cc^{-1}) = b \]

Si può dimostrare inversamente che ogni dominio di integrità finito è un campo.
In un campo è sempre possibile risolvere l’equazione

\[ ax=b \quad \text{ se } a \neq 0 \]

La soluzione unica è \(x =a^{-1}b\) e viene chiamata il quoziente di \(b\) e \(a\). Normalmente viene indicata con \(x = \dfrac{b}{a}\).

Esempio 5.8
L’insieme delle classi residuo \(\mathbb{Z}/p\mathbb{Z}\), dove \(p\) è un numero primo, è un campo.
Infatti abbiamo visto che se \(p\) è un numero primo, allora ogni elemento non nullo di \(\mathbb{Z}/p\mathbb{Z}\) ha un inverso moltiplicativo. Ad esempio nel caso \(\mathbb{Z}/5\mathbb{Z}\) abbiamo

\[ \begin{array}{l} 1 \cdot 1 = 1; \quad 2 \cdot 3 = 1; \quad 4 \cdot 4 = 1 \end{array} \]

---

6) Cifrari a sostituzione monoalfabetica

Il metodo di cifratura a sostituzione monoalfabetica consiste nel sostituire gli elementi base del messaggio in chiaro con altri caratteri, secondo uno schema fisso. La cifratura può essere fatta singolarmente sui singoli caratteri o su gruppi di caratteri. Si possono creare infiniti cifrari di questo tipo, in quanto ogni lettera può essere sostituita con qualsiasi simbolo, non necessariamente con un’altra lettera. Nonostante siano in genere poco efficienti secondo gli standard moderni, rappresentano un passo importante nel processo di sviluppo della Crittografia.

6.1) Cifrari a sostituzione semplice – Il cifrario di Cesare

L’esempio più famoso di codice a sostituzione semplice è il cifrario di Cesare, che si ritiene essere stato usato da Giulio Cesare per comunicare con i suoi ufficiali. In questo caso il messaggio viene crittografato sostituendo ogni lettera con la corrispondente lettera che si trova \(n\) posizioni più avanti nell’alfabeto. Ad esempio prendendo \(n=3\) abbiamo questa corrispondenza:

Per decifrare il messaggio basta fare l’operazione inversa, andando all’indietro nell’alfabeto. Naturalmente bisogna conoscere la chiave, cioè il numero intero positivo \(n\). Se non si conosce la chiave, si può effettuare una ricerca esaustiva provando tutte le \(26\) possibili chiavi, e vedere se il testo cifrato ha un senso. In questo semplice caso quindi occorreranno mediamente \(13\) tentativi per decifrare il testo.
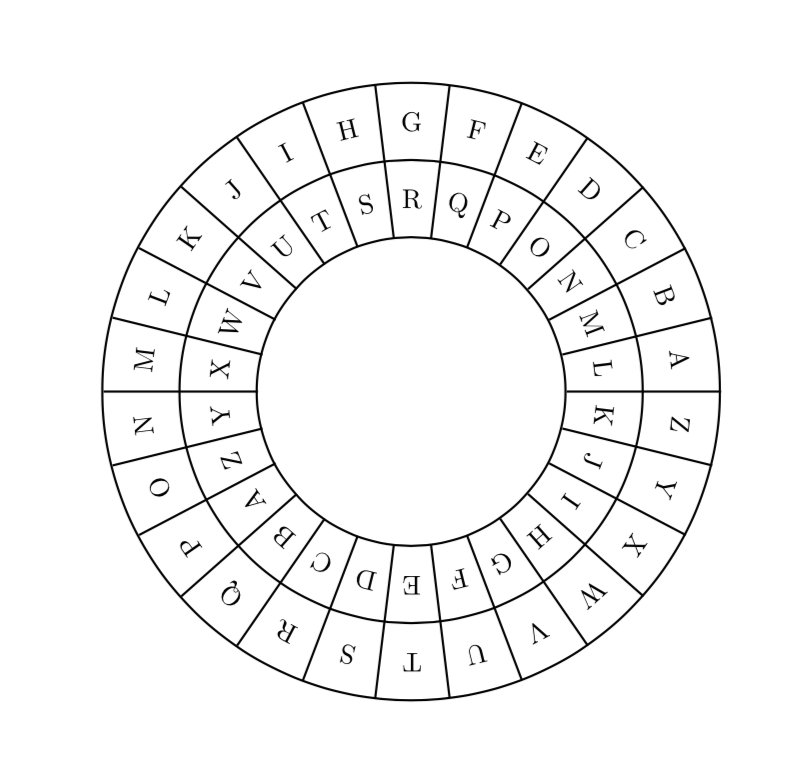
Una realizzazione fisica del cifrario di Cesare è il disco di Leon Battista Alberti (1404-1472), considerato il padre della Crittografia.

Nel disco esterno si trovano le lettere del testo in chiaro e nel disco interno quelle del testo cifrato.
Per rendere più complesso il compito di crittoanalisi si può prendere come chiave una qualunque permutazione delle \(26\) lettere dell’alfabeto. Ad ogni lettera del testo in chiaro può corrispondere quindi nel testo cifrato una qualunque delle lettere dell’alfabeto. In questo caso la chiave è costituita da una stringa di 26 lettere, e il numero di chiavi possibili è \(26! \approx 2^{88}\).
Osserviamo comunque che non tutte le permutazioni sono delle buone scelte, in quanto molte delle lettere del testo in chiaro rimangono invariate.
Lo spazio delle chiavi è talmente grande che anche disponendo di un super computer è molto difficile decifrare il codice con il metodo di forza bruta, cioè effettuando il test su tutte le \(26!\) possibili chiavi.
C’è anche un altro aspetto da considerare: se la crittoanalisi viene fatta tramite un computer, esiste comunque il problema (non semplice) di analizzare in modo automatico se il testo risultante dopo ogni tentativo ha un senso nella lingua utilizzata.
In generale possiamo affermare che, tranne nei casi più semplici, il metodo di forza bruta non è una buona scelta. La Crittoanalisi utilizza metodi più eleganti e sofisticati.

6.2) Crittoanalisi di un codice a sostituzione semplice

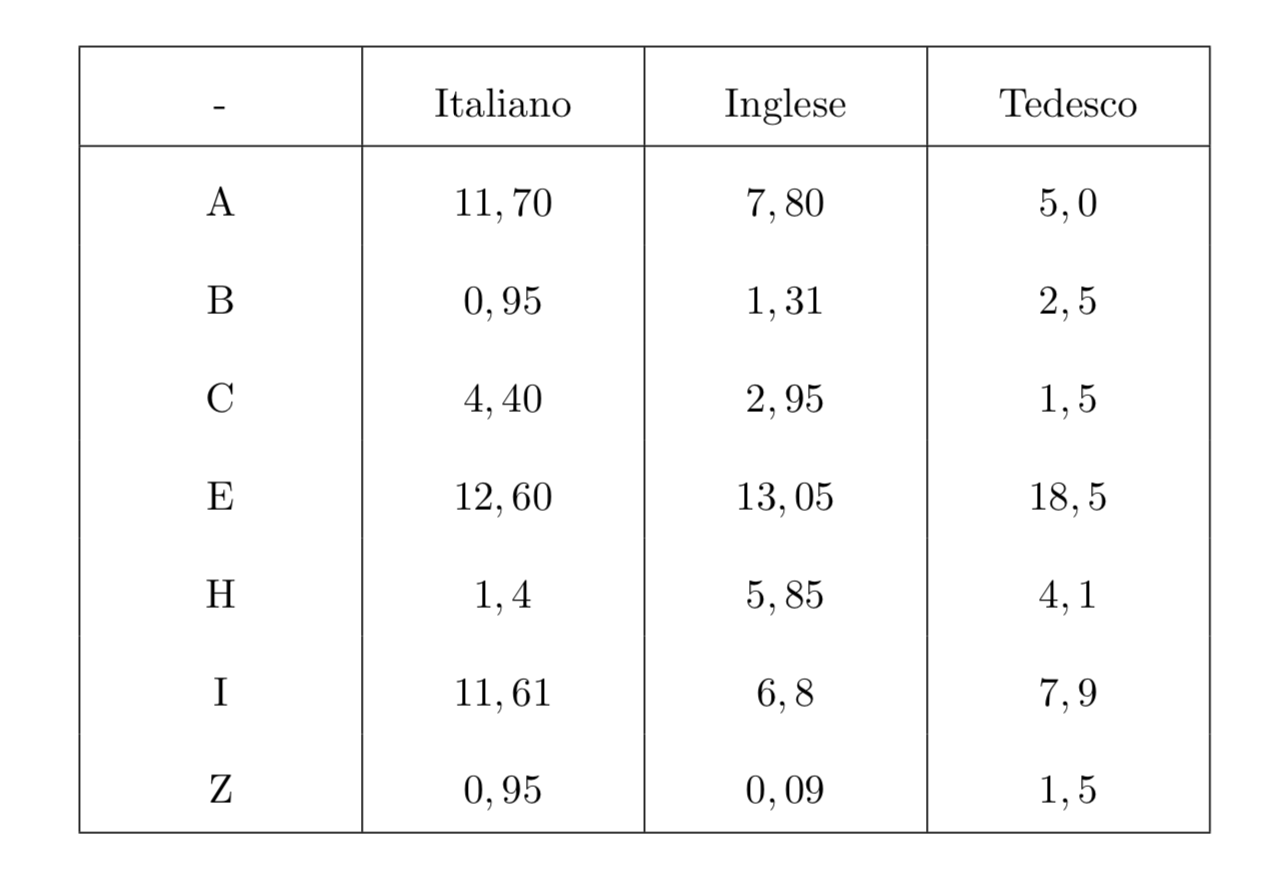
Un metodo molto utilizzato è l’analisi statistica, che consiste nel confrontare le proprietà statistiche (ad esempio la frequenza delle varie lettere) del testo cifrato con le proprietà statistiche del linguaggio utilizzato per il testo in chiaro.
Come è noto in ogni lingua la frequenza di ogni lettera varia di molto. Nella tabella sottostante vediamo le frequenze di alcune lettere in tre lingue diverse:

Oltre ad analizzare le frequenze delle singole lettere, è utile analizzare anche le frequenze dei digrammi e dei trigrammi, cioè combinazioni di due e tre caratteri. Inoltre ogni lingua possiede delle regole speciali che possono essere utili, ad esempio la regola per la lettera \(q\) nella lingua italiana.
Il metodo statistico può essere eseguito tramite dei programmi al computer e in genere ha successo, se i testi da analizzare sono abbastanza lunghi.
Uno spazio di chiavi molto grande non garantisce quindi la sicurezza di un sistema di crittografia. In realtà non c’è mai la certezza che un cifrario, comunque sofisticato, sia sicuro. Al massimo si può dire che è sicuro fino a quando non viene effettuato un attacco con successo.
Non esiste una definizione matematica rigorosa di cifrario sicuro. La presenza di uno spazio di chiavi molto grande da rendere impraticabile una ricerca esaustiva è una condiizone necessaria, ma non sufficiente. Un sistema crittografico ben disegnato deve in aggiunta garantire che non esistano metodi alternativi più brevi di una ricerca esaustiva.

6.3) Cifrari affini

I cifrari a sostituzione semplice sono troppo facili da decifrare, grazie all’analisi statistica e alla disponibilità di computer potenti. Codici più efficienti possono essere creati ricorrendo a delle trasformazioni affini del gruppo delle classi residuo \(\mathbb{Z}/m\mathbb{Z}=\{0,1,2,\cdots,m-1\}\).
Supponiamo di avere un alfabeto di \(m\) caratteri ai quali associamo gli interi \(\{0,1,2,\cdots,m-1\}\). Il numero \(m\) può assumere il valore \(21\) per l’alfabeto italiano, il valore \(26\) per l’alfabeto inglese oppure altri valori, se aggiungiamo alcuni caratteri speciali. Un esempio semplice di cifrario affine è una funzione \(f\) che cifra i caratteri secondo lo schema seguente:

\[ C \equiv aP + b \pmod{m} \]

dove \(a,b\) sono interi, mentre \(P\) corrisponde ad una lettera del testo in chiaro.

Esempio 6.1
Supponiamo di scegliere \(a=5,b=11,m=26\). Allora la codifica della parola \(ROMA\) è \(SDTL\).

Per decifrare un messaggio cifrato con la funzione \(C \equiv aP+b \pmod{m}\) si utilizza la trasformazione inversa:

\[ P \equiv a^{-1}(C-b) \pmod{m} \]

Ricordiamo che l’inverso moltiplicativo \(a^{-1}\) nel gruppo \(\mathbb{Z}/m\mathbb{Z}\) esiste solo se \((a,m)=1\).
Per decifrare il cifrario bisogna conoscere i due parametri \(a,b\). Per questo si può ricorrere all’analisi statistica basata sulla frequenza dei caratteri.

La procedura può essere generalizzata prendendo come singole unità le coppie di caratteri, chiamati digrammi. In questo caso ci sono \(N^{2}\) possibili coppie e la congruenza per cifrare è la seguente:

\[ C \equiv aP + b \pmod{N^{2}} \quad (a,N)=1 \]

Questo tipo di cifrario è un pò più difficile da decifrare rispetto al caso semplice. Un limite è dovuto al fatto che la seconda lettera di ogni coppia cifrata dipende solo dalla seconda lettera della coppia in chiaro. Quindi tramite l’analisi statistica delle frequenze delle lettere nelle posizioni pari si può riuscire a decifrare il testo.

---

7) Cifrari a sostituzione polialfabetica

I cifrari monoalfabetici sono facilmente attaccabili mediante l’analisi statistica delle lettere, in quanto mantengono fissa la relazione fra i simboli in chiaro e i simboli cifrati. In un cifrario polialfabetico a sostituzione viene eliminata questa relazione fissa, rendendo il cifrario meno vulnerabile di fronte ad attacchi basati sulla frequenza dei caratteri.
Il primo esempio di codice polialfabetico venne proposto nel \(1495\) da Leon Battista Alberti nel suo trattato ‘De Cifris’. Il sistema venne creato su richiesta del Vaticano che aveva l’esigenza di trasmettere i messaggi in modo sicuro.
Nel suo trattato Alberti analizza le proprietà statistiche del linguaggio e in particolare la frequenza delle lettere. Consapevole della debolezza dei sistemi di cifratura monoalfabetici, propone un metodo di cifratura polialfabetica. L’implementazione è basata sul disco cifrante visto in precedenza, con alcune modifiche sostanziali. Nel cerchio esterno, fisso, ci sono 24 caselle con i numeri \(1,2,3,4\) e le lettere dell’alfabeto in ordine (escluse le lettere poco frequenti \(H,J,Q,W,Y\)). Nel cerchio interno, mobile, ci sono \(24\) caselle con le lettere dell’alfabeto in ordine casuale, che rappresentano il testo cifrato.
L’algoritmo di Leon Battista Alberti è caratterizzato da un continuo cambio di chiave, che rende inutili gli attacchi basati sulla frequenza dei caratteri. Per i dettagli vedere ^[2].
Il disco cifrante di Leon Battista Alberti, nonostante la sua semplicità, è stato in uso per un periodo di oltre cinquecento anni, durante i quali è stato un riferimento importante nella Crittografia.

7.1) Codice Vigenère

Sulla base delle idee di Alberti il diplomatico francese Blaise de Vigenère (1523-1596) sviluppò nel \(1586\) il cifrario che porta il suo nome.
L’algoritmo di Vigenère richiede due elementi: una parola chiave e il quadrato di Vigenère. Il quadrato di Vigenère consiste di 26 copie dell’alfabeto, ognuna delle quali è ottenuta effettuando uno spostamento a sinistra di una posizione. Di fatto equivale a \(26\) cifrari a sostituzione monoalfabetici simili a quello di Cesare (cifrari additivi).

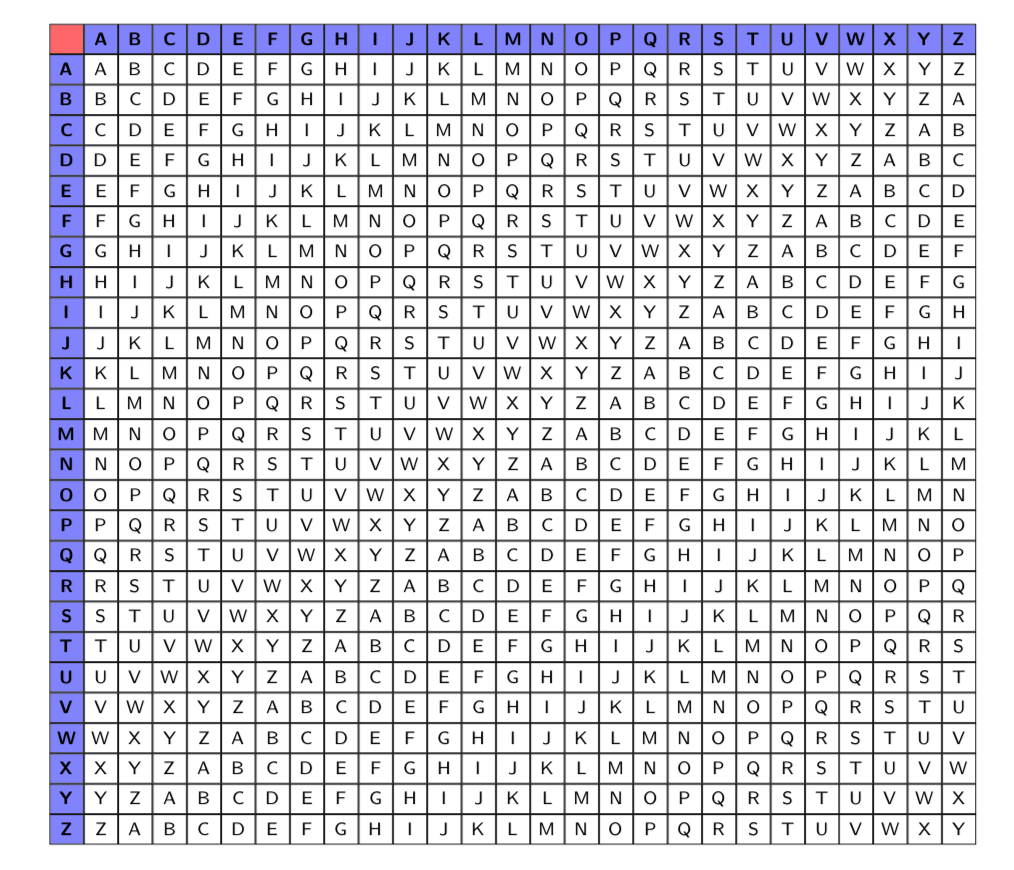
La parola chiave può essere una qualunque sequenza di lettere. L’algoritmo di cifratura di Vigenère è il seguente:

• scrivere ripetutamente le lettere della parola chiave sopra le lettere del testo in chiaro;
• per ogni lettera \(\alpha\) del testo in chiaro, determinare la corrispondente lettera \(\beta\) della chiave che si trova direttamente sopra;
• scegliere la riga del quadrato di Vigenère che inizia con la lettera \(\beta\);
• la lettera cifrata è quella che si trova nell’intersezione con la colonna relativa alla lettera in chiaro \(\alpha\).

Esempio 7.1
Supponiamo di scegliere come parola chiave la stringa “DANTE”. Allora la cifratura del testo “LADIVINACOMMEDIA” è “OAQBZLNNVSPMRWMD”.

Nei paragrafi successivi vedremo come è possibile decifrare il cifrario di Vigenère.

---

8) Cifrari a trasposizione

I cifrari a trasposizione si basano sulla permutazione delle lettere presenti nel testo in chiaro. Nel caso più semplice si fissa un numero intero positivo \(P\), chiamato il periodo della trasposizione. Un esempio con \(P=6\) è:

\[ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 2 & 3 & 5 & 6 & 1 & 4 \\ \end{pmatrix} \]

Il messaggio in chiaro viene scomposto in blocchi di lunghezza \(P=6\) e in ogni blocco le lettere vengono rimescolate secondo la permutazione scelta.
Per decifrare il testo cifrato si utilizza la permutazione inversa.
Con questo algoritmo le frequenze delle lettere sono le stesse del testo in chiaro. Non vengono alterate le lettere effettivamente usate nel testo in chiaro.
Uno schema più complesso è dato dalla trasposizione doppia: le lettere del testo in chiaro vengono scritte sulle righe di una matrice di una data dimensione. Il testo cifrato si ottiene effettuando una permutazione di righe e una permutazione di colonne. Ad esempio supponiamo di crittografie la frase “VENIVIDIVICI” di Giulio Cesare. In primo luogo scriviamo il testo in chiaro sulle righe di una matrice:

\[ \begin{pmatrix} V & E & N & I \\ V & I & D & I \\ V & I & C & I \\ \end{pmatrix} \]

Effettuiamo ora una trasposizione di righe \((1,2,3) \to (3,1,2)\) e poi una trasposizione di colonne \((1,2,3,4) \to (3,4,1,2)\). Abbiamo

\[ \begin{pmatrix} V & E & N & I \\ V & I & D & I \\ V & I & C & I \\ \end{pmatrix} \rightarrow \begin{pmatrix} V & I & D & I \\ V & I & C & I \\ V & E & N & I \\ \end{pmatrix} \rightarrow \begin{pmatrix} D & I & V & I \\ C & I & V & I \\ N & I & V & E \\ \end{pmatrix} \]

Il messaggio cifrato è quindi “DIVICIVINIVE“. La chiave per decifrare il messaggio è costituita dalle dimensioni della matrice e dalle permutazioni di righe e di colonne effettuate. Conoscendo questi elementi si può ricostruire il messaggio originale in chiaro.
Nonostante la sua semplicità questo cifrario è difficile da decifrare, in quanto le proprietà statistiche del testo non vengono conservate nel testo cifrato.
La cifratura a trasposizione può essere resa significativamente più sicura eseguendo la trasposizione in più fasi. Il risultato è ancora una permutazione (più complessa) che risulta più difficile da ricostruire. „
Prima dello sviluppo dei cifrari moderni e dell’utilizzo dei computer sono stati creati i rotori, cioè dispositivi che permettevano la creazione multipla di algoritmi di sostituzione e trasposizione.
La più celebre di queste macchine è l’Enigma, inventata nel 1918 dal tedesco Arthur Scherbius e in seguito migliorata. Venne usata dai tedeschi nel corso della seconda guerra mondiale. Nonostante l’apparente complessità, il funzionamento venne ricostruito da alcuni matematici polacchi. Le loro scoperte vennero comunicate ai servizi inglesi che lavoravano nel campo della Crittoanalisi. Il gruppo inglese che riuscì a decifrare il cifrario era diretto dal matematico Alan Turing, considerato il padre dell’Intelligenza Artificiale.

---

9) Tecniche di crittoanalisi

Scopo della Crittoanalisi è ricostruire il messaggio in chiaro a partire dal messaggio cifrato. Un punto fondamentale della Crittoanalisi moderna è il principio di Kerckhoffs, formulato dall’olandese Auguste Kerckhoffs (1835 – 1903) nel suo libro ‘La criptographie militaire’ (1883).

Il Principio di Kerckhoffs
La segretezza di un sistema crittografico non deve dipendere dalla conoscenza dell’algoritmo utilizzato, ma soltanto dalla segretezza della chiave.

In altre parole si assume che il funzionamento della procedura di cifratura sia completamente pubblico.
A prima vista sembrerebbe che il compito di decifrare un sistema crittografico dovrebbe essere molto più difficile se oltre alla chiave non è noto neanche l’algoritmo. Tuttavia nella realtà è molto difficile che i dettagli di un sistema crittografico rimangano segreti per molto tempo. Inoltre i sistemi moderni basati sul software possono essere decifrati mediante tecniche di reverse engineering. Per verificare quindi la sicurezza di un sistema crittografico non ci si affida alla segretezza dell’algoritmo, ma al contrario l’algoritmo stesso viene reso noto e sottoposto all’analisi approfondita di esperti, al fine di evidenziare eventuali punti deboli.
La crittoanalisi viene svolta dagli hackers per ottenere informazioni in modo illegale, ma è utile anche agli studiosi per analizzare i sistemi informativi e scoprire eventuali punti deboli per la sicurezza.
Possiamo prevedere situazioni diverse nelle quali si trova il crittoanalista:

• Ipotesi 1: conoscenza del solo testo cifrato (known ciphertext attack).
  In questo caso si conosce soltanto un testo cifrato, più o meno lungo.
• Ipotesi 2: conoscenza di un testo in chiaro (known plaintext attack).
  In questo caso si conosce un testo in chiaro e il corrispondente cifrato.
• Ipotesi 3: conoscenza di un testo in chiaro scelto a piacere (chosen plaintext attack).

I sistemi monoalfabetici sono facilmente attaccabili anche nell’ipotesi 1, che è la più debole. Una tecnica efficiente per la crittoanalisi dei cifrari monoalfabetici è l’analisi della frequenza dei vari caratteri del testo.
Introduciamo ora un parametro che è molto importante per la crittoanalisi dei cifrari polialfabetici.

9.1) L’indice di coincidenza

Supponiamo di avere un testo di \(n\) lettere dell’alfabeto e di voler calcolare la probabilità che due lettere scelte in modo casuale dal testo siano uguali. Ricordiamo che il numero totale delle coppie di lettere è \(\dfrac{n(n-1)}{2}\).
Indichiamo con \(n_{1}\) il numero delle lettere \(a\), con \(n_{2}\) il numero delle lettere \(b\), e così via fino a \(n_{26}\), il numero delle lettere \(z\). Per ogni lettera, il numero di coppie della stessa lettera è

\[ \frac{n_{k}(n_{k}-1)}{2}, \quad k=1,2,\cdots, 26 \]

La probabilità che, scegliendo a caso due lettere dal testo, queste siano uguali è quindi

\[ IC = \frac{\sum\limits_{k=1}^{26}n_{k}(n_{k}-1)}{n(n-1)} \]

Il numero IC viene chiamato indice di coincidenza.
L’indice di coincidenza può essere calcolato anche mediante l’analisi statistica del testo. Come è noto ogni lingua, come l’italiano o l’inglese, è caratterizzata da una distribuzione di frequenze delle varie lettere dell’alfabeto. Definiamo ora con \(p_{1},p_{2},\cdots,p_{26}\) le probabilità (frequenze) con cui si presentano le lettere \(a,b,c,\cdots,z\), senza fare distinzioni fra maiuscole e minuscole. Scegliendo a caso in modo indipendente due posizioni in un testo di lunghezza \(n\), la probabilità che in entrambe ci sia la lettera \(a\) è \(p_{1}^{2}\). In realtà dovremmo escludere di scegliere la stessa posizione in entrambe le prove, ma per grandi valori di \(n\) l’errore è trascurabile. Quindi la probabilità che in entrambe le posizioni ci sia una stessa lettera, tra le \(26\) dell’alfabeto, è data dall’indice di coincidenza

\[ IC=\sum\limits_{k=1}^{26}p_{k}^{2} \]

Per la lingua italiana il valore approssimato è \(\text{IC(italiano)} = 0,075\). Per la lingua inglese il valore approssimato è \(\text{IC(inglese)} = 0,068\).
Se invece i caratteri del testo sono generati in modo casuale, allora la probabilità di ogni lettera è \(p_{k}=\dfrac{1}{26}\) e quindi la probabilità che in entrambe le posizioni ci sia una stessa lettera, tra le \(26\) dell’alfabeto, è

\[ \text{IC(casuale)}=\sum\limits_{k=1}^{26}p_{k}^{2}= \sum\limits_{k=1}^{n}\frac{1}{26^{2}} \approx 0,038 \]

L’indice di coincidenza assume un valore maggiore se il testo ha un maggiore grado di irregolarità. Viceversa è minore nel caso della distribuzione uniforme.

Esercizio 9.1
Dimostrare che il valore minimo della somma \(\sum\limits_{k=1}^{26}p_{k}^{2}\) è uguale a \(\dfrac{1}{26} \approx 0,038\).

Suggerimento

\[ \sum\limits_{k=1}^{26}p_{k}^{2}= \frac{1}{26} + \sum\limits_{k=1}^{26}\left(p_{k}- \frac{1}{26}\right)^{2} \]

9.2) Crittoanalisi dei sistemi polialfabetici

Per decifrare gli algoritmi polialfabetici come quello di Vigenère è necessario in primo luogo riuscire a determinare la lunghezza della chiave. Questo permette di scomporre il testo cifrato in un gruppo di cifrari monoalfabetici, per ognuno dei quali è possibile utilizzare l’analisi statistica basata sulle frequenze.

9.2.1) Il test di Kasiski

Questo test venne pubblicato nel \(1863\) da Friedrich Kasiski, anche se era già stato usato alcuni anni prima da Charles Babbage, maggiormente noto per i suoi lavori che anticiperanno l’avvento dei computer.
L’idea base del test di Kasiski è che se due sequenze uguali di lettere si trovano ad una distanza che è un multiplo della lunghezza della chiave, allora anche le sequenze corrispondenti nel testo cifrato sono uguali. Il metodo di Kasiski si basa quindi sulla ricerca di sequenze di lettere che si ripetono nel testo cifrato.
Se le sequenze si ripetono nel testo cifrato, allora si ipotizza che la loro distanza è un multiplo della lunghezza della chiave.

Esempio 9.1
La tabellina sotto illustra il concetto alla base del test di Kasiski. La parola chiave è “CASA”, quindi la distanza è uguale a \(4\).

Perciò se si trovano parole ripetute si può supporre che siano delle cifrature dello stesso testo in chiaro. Naturalmente può essere una ipotesi errata, tuttavia spesso funziona, in quanto nei testi normali molte parole si ripetono.
Una volta che si è riusciti a determinare la lunghezza della chiave, si può scomporre il testo cifrato polialfabetico in un insieme di testi monoalfabetici. Ad ognuno di questi può essere applicata l’analisi statistica della frequenza delle lettere e quindi determinare la sua chiave.
Nel paragrafo seguente illustriamo in dettaglio il test di Friedman, che fornisce una formula per il calcolo approssimato della lunghezza della chiave.

9.2.2) Il test di Friedman per la crittoanalisi del cifrario di Vigenère

Questo metodo è stato proposto nel \(1925\) dal crittologo americano William Friedmann. Il metodo di Friedmann è un test statistico basato sulla frequenza delle lettere. Come strumento Friedman utilizza l’indice di coincidenza, che come abbiamo visto serve per determinare la probabilità che due lettere scelte a caso da un testo siano uguali.
Nel caso di un cifrario monoalfabetico la distribuzione di probabilità è la stessa nel testo in chiaro e in quello cifrato, in quanto si tratta di una semplice permutazione delle lettere. Quindi l’indice di coincidenza rimane invariato. Nel caso dei cifrari polialfabetici l’indice di coincidenza diminuisce, in quanto le frequenze delle lettere tendono ad uguagliarsi.
Questo permette di determinare se un cifrario è monoalfabetico o polialfabetico.
Una volta stabilito che si tratta di un cifrario polialfabetico, ad esempio di Vigenère, si tratta di determinare la lunghezza della chiave, che dipende dalla differenza fra l’indice di coincidenza del testo in chiaro, ad esempio \(0,075\) per la lingua italiana, e l’indice di coincidenza calcolato per il testo cifrato.
Supponiamo di avere un testo di lunghezza \(n\) e ordiniamo le lettere su \(L\) colonne, dove \(L\) è la lunghezza della chiave. Ogni colonna ne contiene quindi \(n/L\), trascurando errori di arrotondamento. L’esempio sottostante utilizza la parola chiave “DANTE” e il testo in chiaro “NELMEZZODELCAMMINDINOSTRAVITA”:

Le lettere di ogni colonna sono cifrate con un cifrario monalfabetico; quindi, supponendo di utilizzare la lingua italiana, la probabilità che due lettere scelte a caso in una colonna siano uguali è \(p_{it} \approx 0,075\). Se prendiamo due lettere su colonne diverse allora la probabilità sarà molto più piccola, supponiamo il minimo assoluto \(p_{min}\approx 0,038\). Il test di Friedman consiste nel determinare la probabilità che due lettere scelte a caso siano uguali. Prendiamo a caso una tra le \(n\) lettere; per calcolare il valore medio delle coppie di lettere uguali dobbiamo distinguere fra la colonna in cui si trova la lettera che abbiamo scelto e le altre \(L-1\) colonne. È facile vedere che il valore medio atteso \(M\) del numero delle coppie di lettere uguali è

\[ M = \frac{n(n-L)}{2L}\cdot p_{it}+ \frac{n^{2}(L-1)}{2L}\cdot p_{min} \ , \]

dove \(p_{it}=0,075\) e \(p_{min}=0,038\).

Per calcolare la probabilità che una coppia contenga due lettere uguali, e quindi l’indice di coincidenza, basta dividere per il numero totale delle coppie. Tale probabilità è quindi:

\[ \frac{2M}{n(n-1)} \]

Questa probabilità è approssimativamente uguale all’indice di coincidenza. Quindi effettuando i calcoli otteniamo la formula di Friedman per la lunghezza della chiave:

\[ L = \frac{0,037n}{(n-1)IC – 0,038n + 0,075} \ , \]

dove \(IC = \dfrac{\sum_{k=1}^{26}n_{k}(n_{k}-1)}{n(n-1)}\).

Naturalmente spesso non verrà un numero intero. Tuttavia la lunghezza effettiva della chiave sarà in genere l’intero più vicino.
Una volta determinata la lunghezza, si può determinare il valore della chiave. La prima lettera della chiave può essere determinata analizzando le lettere nelle colonne \(1,L+1,2L+1,\cdots\), che sono cifrate con lo stesso cifrario monoalfabetico. Lo stesso procedimento si segue per le altre lettere della chiave.

---

Conclusione

In questo articolo abbiamo esaminato alcuni semplici algoritmi di crittografia e crittoanalisi. In articoli successivi studieremo alcuni algoritmi più complessi attualmente in uso, sia per la crittografia simmetrica, sia per la crittografia a chiave pubblica.

---

Bibliografia

^[1]David Kahn – The Codebreakers (Scribner, Rev Sub edition; December 5, 1996)

^[2]Leon Battista Alberti – Il De Cifris di Leon Battista Alberti (Galimberti; Torino, 1464−2009)

^[3]Simon Singh – The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography (Anchor, 2000)

^[4]J. Kraft, L. Washington – An Introduction to Number Theory with Cryptography (Chapman and Hall, 2018)