Gli Interi di Gauss e le Somme di due Quadrati

In questo articolo studieremo il problema della rappresentazione degli interi come somma di quadrati. Il problema consiste nel determinare sotto quali condizioni un intero positivo \(n\) si può scrivere come somma di due quadrati di interi, cioè nella forma

\[ n = x^{2}+ y^{2} \ , \quad x,y \in \mathbb{Z} \]

Alcuni esempi sono i seguenti:

\[ \begin{array}{l} 1 = 0^{2}+ 1^{2} \\ 5 = 2^{2}+1^{2} \\ 13 = 2^{2}+ 3^{2} \\ 20 = 2^{2}+ 4^{2} \\ 65 = 1^{2} + 8^{2} \\ 85=2^{2}+ 9^{2}=6^{2}+7^{2} \end{array} \]

Tuttavia per altri interi questa rappresentazione non è possibile. Ad esempio non è possibile per i seguenti numeri:

\[ 3,6,7,11,12,14,15,\cdots \]

Il matematico francese Albert Girard (1595-1632) fu il primo ad affermare – senza tuttavia dare una dimostrazione – che ogni numero primo della forma \(4k+1\) è rappresentabile come somma di due quadrati. Fermat (1601-1665) affermò di avere una dimostrazione, senza tuttavia pubblicarla. La prima dimostrazione fu pubblicata nel \(1747\) da Eulero.
In questo articolo studieremo i teoremi di Fermat ed Eulero; a tal fine introdurremo le proprietà aritmetiche degli interi di Gauss, che costituiscono uno strumento molto utile per questo tipo di problemi.

---

1) Le strutture algebriche: i gruppi e gli anelli

Un’operazione binaria su un insieme \(G\) è una funzione che ad ogni coppia di elementi di \(G\) associa un unico elemento di \(G\). L’operazione binaria può essere di vario tipo: addizione, moltiplicazione, composizione di funzioni, ecc. Associando delle operazioni binarie ad un insieme otteniamo una struttura algebrica. In questo contesto ricordiamo le definizioni delle strutture algebriche di gruppo e anello.

Definizione 1.1 – Gruppi
Un gruppo consiste in un insieme \(G\) sul quale è definita una operazione binaria \(\cdot : G \times G \to G\), tale che siano soddisfatte le seguenti proprietà:

\[ \begin{array}{l} a \cdot b \in G \quad \forall a,b \in G \\ a \cdot (b \cdot c) = (a \cdot b) \cdot c \quad \forall a,b,c \in G \\ \exists{e} \in G \quad \text{tale che } a \cdot e = a \quad \textbf{(elemento neutro)}\\ \forall a \in G \quad \exists{b}\in G \quad \text{tale che} \quad a \cdot b = e \quad \textbf{(elemento inverso)}\\ \end{array} \]

Un gruppo si dice commutativo o abeliano se

\[ a \cdot b= b \cdot a \quad \forall a,b \in G \]

Per indicare l’operazione binaria di un gruppo si possono utilizzare simboli qualsiasi. Tuttavia nel caso di gruppi riguardanti gli insiemi numerici si utilizzano in genere i simboli \(+,\cdot\) per le operazioni binarie di addizione e moltiplicazione, per gli elementi neutri si utilizzano rispettivamente i simboli \(0,1\) e per l’inverso di un elemento \(a\) si usa il simbolo \(-a\) oppure \(a^{-1}\).

Esempio 1.1
I seguenti sono gruppi abeliani:

\[ \begin{array}{l} (\mathbb{Z};+) \quad \text{l’insieme degli interi rispetto alla operazione di addizione} \\ (\mathbb{Q};+) \quad \text{l’insieme dei numeri razionali rispetto alla operazione di addizione} \\ (\mathbb{Q}\setminus{0};\cdot) \quad \text{l’insieme dei numeri razionali non nulli rispetto all’operazione di moltiplicazione} \\ \end{array} \]

Esempio 1.2
Indichiamo con \(M(2,\mathbb{Z})\) l’insieme delle matrici quadrate \(2 \times 2\), con elementi interi. La somma di due matrici \(A=\{a_{ij}\}\) e \(B=\{b_{ij}\}\) è così definita:

\[ A+B= \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ \end{pmatrix} = \begin{pmatrix} a_{11}+ b_{11} & a_{12}+b_{12} \\ a_{21}+b_{21} & a_{22}+b_{22} \\ \end{pmatrix} \]

Tale insieme è un gruppo rispetto alla operazione di somma di due matrici. L’elemento neutro rispetto all’operazione di somma è la matrice nulla, con tutti i coefficienti uguali a zero.
Naturalmente sono dei gruppi algebrici anche le strutture \(M(2,\mathbb{Q})\), \(M(2,\mathbb{R})\), \(M(2,\mathbb{C})\).

Definizione 1.2 – Anelli e domini di integrità
Sia \(R\) un insieme non vuoto nel quale sono definite due operazioni binarie, che chiamiamo addizione e moltiplicazione e indichiamo con i simboli \(+,\cdot\). La struttura \((R;+,\cdot)\) è un anello se sono verificate le seguenti proprietà:

\[ \begin{array}{l} (R;+) \quad \text{è un gruppo abeliano con l’operazione di addizione} \\ a \cdot (b \cdot c) = (a \cdot b) \cdot c \quad \forall a,b,c \in R \quad \textbf{(proprietà associativa)} \\ a \cdot (b + c) = a \cdot b+ a \cdot c \quad \forall a,b,c \in R \quad \textbf{(proprietà distributiva)} \\ \end{array} \]

Un anello si dice commutativo se risulta

\[ a \cdot b = b \cdot a \quad \forall a,b \in R \]

L’elemento neutro rispetto alla operazione di addizione viene indicato con il simbolo \(0\). Per ogni anello risulta quindi:

\[ a + 0 = 0+ a \quad \forall a \in R \]

Un anello si chiama anello unitario o con unità se esiste un elemento neutro rispetto alla moltiplicazione. Tale elemento si indica con il simbolo \(1\). Per un anello con unità abbiamo quindi:

\[ a \cdot 1 = 1 \cdot a \quad \forall a \in R \]

Un elemento \(a \in R\) di un anello unitario si chiama unità se esiste un elemento \(b \in R\) tale che \( a \cdot b =1\). L’elemento \(b\) si chiama inverso di \(a\), e viene indicato con \(a^{-1}\).
L’insieme degli interi \(\mathbb{Z}\) è l’esempio fondamentale di anello commutativo con unità, con le usuali operazioni di addizione e moltiplicazione. L’elemento neutro rispetto alla moltiplicazione è il numero \(+1\). Gli unici elementi unità di \(\mathbb{Z}\) sono i numeri \(+1,-1\).
Un anello commutativo si chiama dominio di integrità se non ha divisori dello zero, cioè se il prodotto di due elementi non nulli è non nullo. In termini equivalenti se vale la legge di cancellazione del prodotto:

\[ a \cdot b = 0 \implies a=0 \lor b=0 \quad \forall a,b \in R \]

Esercizio 1.2 – Anello delle matrici
Date due matrici \(A,B \in M(2,\mathbb{R})\), oltre all’operazione di addizione, possiamo definire anche l’operazione di prodotto nel seguente modo:

\[ A \cdot B = \left( \begin{array}{cc} a & b \\ c & d \\ \end{array} \right) \cdot \left( \begin{array}{cc} e & f \\ g & h \\ \end{array} \right) = \left( \begin{array}{cc} ae+bg & af + bh\\ ce+dg & cf + dh\\ \end{array} \right) \]

Dimostrare che \(M(2,\mathbb{R})\) è un anello unitario non commutativo. Determinare la matrice neutra rispetto alla moltiplicazione. Trovare un esempio di due matrici \(A,B\) tali che \( A \cdot B \neq B \cdot A\).
Infine trovare un esempio di due matrici non nulle \(A,B\) tali che \(A \cdot B = 0\), dimostrando quindi che l’anello \(M(2,\mathbb{R})\) non è un dominio integrità.

---

2) Gli interi di Gauss

Definizione 2.1
Gli interi di Gauss sono i numeri complessi che appartengono al seguente insieme:

\[ \mathbb{Z}[i]= \{a + bi \in \mathbb{C}: a,b \in \mathbb{Z}\} \]

dove \(i\) è l’unità immaginaria tale che \(i^{2}=-1\).
Essendo un sottoinsieme del campo dei numeri complessi, è facile dimostrare che gli interi di Gauss formano un anello commutativo con unità. L’unità per la moltiplicazione è chiaramente il numero \(\alpha=1+0i\). Inoltre, è ovviamente un dominio di integrità.
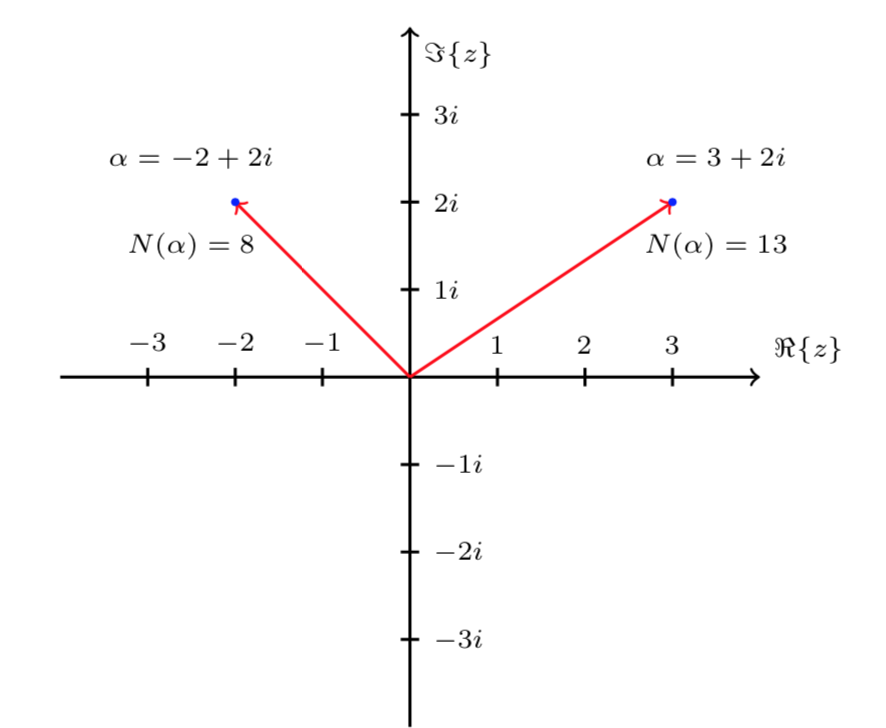
Dato \(\alpha = a+bi\) un intero di Gauss, il coniugato di \(\alpha\) è il numero \(\overline{\alpha}=a-bi\). La norma di \(\alpha\) è la seguente

\[ N(\alpha) = \alpha \overline{\alpha}= a^{2}+b^{2}=|\alpha|^{2} \]

Possiamo rappresentare gli interi di Gauss come vettori del piano, con l’origine del punto \((0,0)\) e con il vertice nei punti a coordinate intere (reticolo degli interi). La norma corrisponde al quadrato della lunghezza del vettore e si calcola con il teorema di Pitagora.

Esercizio 2.1
Dimostrare che la norma è una funzione moltiplicativa, cioè:

\[ N(\alpha \beta) = N(\alpha)N(\beta) \quad \forall \alpha,\beta \in \mathbb{Z}[i] \]

Definizione 2.2
Un elemento \(\alpha\) di \(\mathbb{Z}[i]\) si chiama unità se \(N(\alpha)=1\).
Due interi di Gauss si dicono associati se possono essere ottenuti ognuno dall’altro moltiplicato per una unità. Il concetto è simile a due interi ordinari che differiscono per il segno.

Esercizio 2.2
Dimostrare che le unità di \(\mathbb{Z}[i]\) sono solamente gli interi di Gauss \(\pm 1,\pm i\).

Esercizio 2.3
Dimostrare che un elemento \(\alpha \in \mathbb{Z}[i]\) è un’unità se e solo se è invertibile, cioè se esiste un intero di Gauss \(\beta\) tale che \(\alpha\beta=1\).

2.1) Divisibilità e primi di Gauss

Le nozioni di divisibilità definite per gli interi ordinari \(\mathbb{Z}\) possono essere estese in modo naturale anche per gli interi di Gauss.

Definizione 2.3
Siano dati due interi di Gauss \(\alpha,\beta\). Si dice che \(\alpha\) divide \(\beta\) se risulta

\[ \beta = \alpha \gamma \ , \quad \gamma \in \mathbb{Z}[i] \]

Esempio 2.1
Verificare che \(4+4i\) divide \(-4+12i\).
Verificare che \(1+5i\) non divide \(1+3i\).

Esercizio 2.4
Siano dati due interi di Gauss \(\alpha,\beta\). Allora

\[ \beta | \alpha \implies N(\beta)|N(\alpha ) \]

Esercizio 2.5
Un intero di Gauss \(\alpha=a+bi\) è divisibile da un intero ordinario \(n\) se e solo se \(n|a\) e \(n|b\).

Due interi di Gauss si dicono relativamente primi fra loro se gli unici divisori comuni sono delle unità.

2.2) Algoritmo di Euclide in \(\mathbb{Z}[i]\)

Ricordiamo il lemma di divisione di Euclide nell’anello degli interi ordinari \(\mathbb{Z}(+,\cdot)\).

Teorema 2.1 – Euclide
Dati due interi ordinari \(a,b\), esistono due unici interi ordinari \(q,r\) tali che

\[ a= bq + r \ , \quad 0 \le r \lt b \]

Per la dimostrazione si può vedere l’articolo su questo blog.
Sulla base del teorema precedente viene realizzato l’algoritmo di Euclide, che permette di calcolare il massimo comune divisore fra due interi ordinari.
Nell’anello degli interi di Gauss \(\mathbb{Z}[i]\) vale un teorema simile:

Teorema 2.2
Siano due interi di Gauss \(\alpha,\beta\) non nulli. Allora esistono un quoziente \(\gamma \in \mathbb{Z}[i]\) e un resto \(\rho \in \mathbb{Z}[i]\) tali che:

\[ \alpha = \beta \gamma + \rho \quad \text{ dove } N(\rho) \lt N(\beta) \]

In base a questa prorpietà si dice che l’anello \(\mathbb{Z}[i]\) è un dominio euclideo.

Dimostrazione
Per determinare il quoziente \(\gamma\) e il resto \(\rho\) in primo luogo calcolare il valore del numero complesso \(\dfrac{\alpha}{\beta}\). Questo numero si troverà in una delle celle del reticolo fondamentale del piano, sui vertici del quale si trovano gli interi di Gauss. Quindi possiamo sempre scegliere uno degli interi di Gauss che si trova a distanza inferiore all’unità dal numero complesso \(\dfrac{\alpha}{\beta}\). Questo intero di Gauss è il quoziente \(\gamma\). Il resto è \(\rho= \alpha -\beta \gamma \). Ovviamente \(N(\rho) \lt N(\beta)\).

Esempio 2.2
Dati \(\alpha= 2+7i\), \(\beta=1+2i\). Abbiamo

\[ \frac{2+7i}{1+2i}=\frac{(2+7i)(1-2i)}{1+4}= \frac{16+3i}{5} \]

In questo caso possiamo scegliere \(\gamma=3+i\). Quindi

\[ (2+7i)=(1+2i)(3+i) +1 \]

Anche nell’anello degli interi di Gauss si può utilizzare l’algoritmo di Euclide per determinare il massimo comune divisore fra due numeri.

Definizione 2.4 – Massimo comune divisore
Un elemento \(\delta \in \mathbb{Z}[i]\) si dice un massimo comune divisore di due interi di Gauss \(\alpha,\beta\) se

• \(\delta |\alpha \) e \(\delta | \beta\)
• ogni altro divisore comune di \(\alpha\) e \(\beta\) divide \(\delta\)

Si può dare una definizione equivalente:
Un massimo comune divisore di \(\alpha,\beta\) è un divisore comune con la massima norma.

Notiamo che se \(\delta\) è un massimo comune divisore e \(\varepsilon\) è un’unità, allora anche il prodotto \(\varepsilon \delta\) è un massimo comune divisore.

Teorema 2.3 – Algoritmo di Euclide
Dati due interi di Gauss \(\alpha,\beta\) applicare l’algoritmo specificato nel seguente schema di divisioni, fino a raggiungere un resto nullo:

\[ \begin{array}{l} \alpha = \beta \gamma_{1} + \rho_{1} \quad N(\rho_{1}) \lt N(\beta) \\ \beta = \rho_{1} \gamma_{2} + \rho_{2} \quad N(\rho_{2}) \lt N(\rho_{1}) \\ \rho_{1} = \rho_{2} \gamma_{3} + \rho_{3} \quad N(\rho_{3}) \lt N(\rho_{2}) \\ \vdots \\ \rho_{k} = \rho_{k+1} \gamma_{k+2} + \rho_{k+2} \quad N(\rho_{k+2}) \lt N(\rho_{k+1}) \\ \rho_{k+1} = \rho_{k+2} \gamma_{k+3} + 0 \\ \vdots \end{array} \]

Il massimo comune divisore di \(\alpha\) e \(\beta\) è l’ultimo resto non nullo.

Esempio 2.3
Siano dati \(\alpha=-21+18i\) e \(\beta=-13-i\). Calcoliamo il \(MCD(\alpha,\beta\)).

\[ \begin{array}{l} \frac{-21-18i}{-13-i}=\frac{(-21-18i)(-13+i)}{(-13-i)(-13+i)}=\frac{3}{2}- \frac{3}{2}i \\ \end{array} \]

Scegliamo quindi \(\gamma= 1-i\). Proseguendo con lo stesso procedimento troviamo \(MCD(\alpha,\beta)=-7+6i\).

2.3) I numeri primi di Gauss

Definizione 2.5
Sia \(\pi\) un intero di Gauss tale che \(N(\pi) \gt 1\). Allora

• \(\pi\) si dice primo di Gauss se \(\pi | \alpha \beta \implies \pi |\alpha \lor \pi | \beta\)
• \(\pi\) si dice irriducibile se i suoi divisori sono soltanto le unità e gli associati di \(\pi\)

Se un intero di Gauss non è primo, allora si dice composto. Vale il seguente teorema:

Teorema 2.4
Un intero di Gauss è irriducibile se e solo se è un primo di Gauss.

In base al teorema precedente possiamo affermare che un intero di Gauss \(\alpha\) è un primo di Gauss se non è un’unità e gli unici divisori sono:

\[ \pm 1, \pm i, \pm \alpha, \pm i \alpha \]

Esempio 2.4
Il numero intero \(5\) non è un primo di Gauss in quanto \(5=(2+i)(2-i)\).

Esercizio 2.6
Dimostrare che i numeri \(\alpha=1+i\) e \(\beta=1-i\) sono primi di Gauss.

Esercizio 2.7
Dimostrare che i numeri \(\alpha=2+5i\) e \(\beta=4+i\) sono primi di Gauss.

Un criterio per riconoscere i primi di Gauss è dato dal seguente teorema:

Teorema 2.5
Se \(N(\pi)\) è un numero primo ordinario in \(\mathbb{Z}\), allora \(\pi\) è un primo di Gauss.

Dimostrazione
Supponiamo \(\pi = \alpha \beta\). Allora \(N(\pi)=N(\alpha)N(\beta)\). Quindi abbiamo \(N(\alpha)=1\) oppure \(N(\beta)=1\), da cui segue che \(\pi\) è irriducibile.

Esempio 2.5
Il numero \(2+3i\) è un numero primo. Lo stesso vale per i suoi associati: \(-2-3i,-2i+3,2i-3\).

Il teorema precedente fornisce una condizione sufficiente che tuttavia non è necessaria, cioè esistono primi di Gauss la cui norma non è un primo ordinario, come vediamo nel seguente esempio.

Esempio 2.6
Il numero \(3\), con \(N(3)=9\), è un numero primo di Gauss. Se non fosse primo si avrebbe \(3=(\alpha + i \beta)\gamma + i \delta\). Ma allora si avrebbe

\[ 9=(\alpha^{2}+\beta^{2})(\gamma^{2}+\delta^{2}) \]

Poiché il numero \(3\) non può essere somma di due quadrati, la relazione precedente implica che \(\alpha^{2}+\beta^{2}=1\) oppure \(\gamma^{2}+\delta^{2}=1\), e quindi uno dei due fattori è un’unità.

Ovviamente se un numero intero ordinario è un primo di Gauss, allora è anche un primo ordinario. Tuttavia non vale non vale il viceversa. Ad esempio

\[ 17 = (4+i)(4-i) \]

Esercizio 2.8
Dimostrare che il numero \(2\) non è un primo di Gauss.

Esercizio 2.9
Dimostrare che non esistono interi di Gauss la cui norma è del tipo \(4n+3\).

Suggerimento
Dimostrare che che la somma di due quadrati non può essere del tipo \(4n+3\).

Esercizio 2.10
Dimostrare che se \(p=4n+3\) è un primo ordinario in \(\mathbb{Z}\) allora è anche un primo di Gauss.

Mediante i teoremi precedenti si può dimostrare il teorema fondamentale dell’aritmetica nell’anello \(\mathbb{Z}[i]\):

Teorema 2.6 – Esistenza della fattorizzazione
Sia \(\alpha \in \mathbb{Z}[i]\) un intero di Gauss non nullo e diverso da una unità. Allora è possibile esprimere \(\alpha\) come prodotto finito di primi di Gauss.

Come per gli interi ordinari la fattorizzazione è unica.

Teorema 2.7 – Unicità della fattorizzazione
Sia \(\alpha \in \mathbb{Z}[i]\) un intero di Gauss non nullo e diverso da una unità. La fattorizzazione è unica, fatta eccezione per l’ordine, la presenza di unità, e la possibile ambiguità dovuta alla presenza di associati di numeri primi.

In base al teorema precedente l’anello \(\mathbb{Z}[i]\) è anche un Dominio a Fattorizzazione Unica (UFD).
Infine ricordiamo il seguente teorema che riassume i risultati precedenti e permette di identificare tutti i numeri primi di Gauss:

Teorema 2.8
A meno di numeri associati, i numeri primi di Gauss sono i seguenti:

• \(1+i\) con norma uguale a \(2\)
• i numeri primi ordinari \(q \equiv 3 \pmod{4}\) con norma \(q^{2}\)
• \(a \pm ib\) con \(p=a^{2}+b^{2}\) primo ordinario del tipo \(p \equiv 1 \pmod{4}\)

Per approfondire lo studio degli interi di Gauss e per una introduzione alla teoria algebrica dei numeri vedere ad esempio ^[1].

---

3) Rappresentazione di interi come somma di due quadrati

Definizione del problema
Dato un intero positivo \(n\), determinare se esiste una rappresentazione come somma di due quadrati di interi, cioè

\[ n = a^{2}+ b^{2} \ , \quad a,b \in \mathbb{Z} \]

Una rappresentazione si dice primitiva se \((a,b)=1\). Si contano come distinte anche le rappresentazioni che differiscono per l’ordine o per il segno. Inoltre, è ammessa anche la presenza dello zero.
Oltre a stabilire se esiste almeno una rappresentazione come somma di quadrati, esiste il problema collegato di determinare il numero delle diverse rappresentazioni possibili per ogni fissato \(n\).
Un formulazione equivalente del problema mediante gli interi di Gauss è la seguente.

• Quali interi positivi \(n\) possono essere norme di interi di Gauss?
• Dato un intero positivo \(n\), determinare tutti gli interi di Gauss \(\alpha\) tali che \(N(\alpha)=n\).

Anche il numero zero è ammesso tra i valori di \(a,b\). Vediamo alcuni esempi:

\[ \begin{array}{l} 17 = 4^{2}+ 1^{2} \\ 50 = 5^{2}+ 5^{2} \\ 16 = 4^{2} + 0^{2} \\ 25= 5^{2}+0^{2}=3^{2}+4^{2}\\ \end{array} \]

Non tutti gli interi possono essere rappresentati come somma di due quadrati di interi. Alcuni esempi sono i numeri \(7,11,19\).
Per studiare il problema ricordiamo in primo luogo la seguente identità, già dimostrata da Diofanto di Alessandria.

Teorema 3.1 – Diofanto

\[ (a^{2}+b^{2})(c^{2}+d^{2}) = (ac-bd)^{2}+(ad+bc)^{2} \]

Questa formula è nota anche come identità di Brahmagupta-Fibonacci.

Dimostrazione
Per dimostrare l’identità si possono svolgere i calcoli eliminando le parentesi e quindi verificare l’uguaglianza dei due membri.
In realtà l’identità deriva direttamente dalle proprietà della moltiplicazione di due numeri complessi. Dati \(z=a+bi\) e \(w=c+di\), abbiamo

\[ \begin{array}{l} |z|^{2}=z \overline{z}=a^{2}+b^{2} \\ zw =(ac-bd)+(ad+bc)i \\ |zw|^{2}=zw \overline{zw}=|z|^{2}|w|^{2} \\ \end{array} \]

La terza formula è equivalente all’identità di Diofanto.
Dall’identità di Diofanto deriva quindi che se due numeri sono rappresentabili some somma di quadrati, lo è anche il loro prodotto.

Esercizio 3.1
Dato il numero \(493=17 \cdot 29\), determinare la sua rappresentazione come somma di due quadrati, applicando l’identità di Diofanto.

Risposta: \(493=13^{2}+ 18^{2}\)

3.1) Numeri primi somma di due quadrati

Vediamo ora alcuni teoremi di Fermat che stabiliscono le condizioni necessarie e sufficienti affinché un numero intero abbia almeno una rappresentazione come somma di due quadrati. Analizziamo prima il problema della rappresentazione dei numeri primi come somma di due quadrati. È sufficiente considerare soltanto i numeri primi dispari, poiché chiaramente \(2=1^{2}+1^{2}\).
Ricordiamo prima il seguente teorema:

Teorema 3.2
Sia \(p\) un numero primo dispari. Allora la congruenza

\[ x^{2}+1 \equiv 0 \pmod{p} \]

ammette soluzioni se solo se \(p \equiv 1 \pmod{4}\), cioè se \(p\) è del tipo \(p=4k+1\).

Dimostrazione
Chiaramente \(x=0\) non è una soluzione. Supponiamo ora \(p=4k+3\). Possiamo scrivere \(t=\dfrac{p-1}{2}=2k+1\), con \(t\) numero dispari. Elevando entrambi i membri dell’equazione alla potenza \(t\) abbiamo \(x^{p-1} \equiv 1 \pmod{p}\) per il piccolo teorema di Fermat e quindi abbiamo una contraddizione in quanto \( 1 \equiv -1 \pmod{p}\) solo se \(p=2\).
Supponiamo ora \(p=4k+1\). Allora abbiamo

\[ \begin{array}{l} 4k=p-1 \equiv -1 \pmod{p} \\ 4k-1 =p-2 \equiv -2 \pmod{p} \\ \vdots \\ 2k+1=p-2k \equiv -2k \pmod{p} \\ \end{array} \]

Ricordando il teorema di Wilson \((p-1)! \equiv -1 \pmod{p}\), abbiamo

\[ \begin{array}{l} (4k)!\equiv (-1)(-2) \cdots (-2k)(2k)(2k-1) \cdots 2 \cdot 1= \\ [(2k)!]^{2}(-1)^{2k} \equiv -1 \pmod{p} \end{array} \]

Quindi il numero \(x=(2k)!\) è soluzione dell’equazione \(x^{2}+1 \equiv 0 \pmod{p}\).

Nota
Il teorema 3.2 può essere formulato usando la notazione del simbolo di Legendre della teoria dei residui quadratici:

Teorema 3.2 (seconda versione)
Il numero intero \(-1\) è un residuo quadratico dei primi della forma \(p=4k+1\) e un non-residuo quadratico dei primi della forma \(p=4k+3\), cioè

\[ \left (\frac{-1}{p}\right) =\left(-1 \right)^{\dfrac{p-1}{2}} \]

Per la teoria dei residui quadratici si può vedere l’articolo in questo blog.

Teorema 3.3 – Eulero
Un numero primo \(p\) dispari può essere espresso come somma di due quadrati se e solo se è della forma \(p \equiv 1 \pmod{4}\). In simboli

\[ p=x^{2} + y^{2} \quad \text{se e solo se } p=4k+1 \]

Dimostrazione
Osserviamo che il quadrato di un numero pari è divisibile per \(4\), mentre il quadrato di un numero dispari è congruente a \(1 \pmod {4}\), cioè il resto della divisione per \(4\) è uguale a \(1\). Quindi la somma di due quadrati può avere resto uguale a \(0,1,2\) ma non \(3\) nella divisione per \(4\). Da ciò deriva che un primo della forma \(p=4k+3\) non può essere espresso come somma di due quadrati.
Quindi se \(p=x^{2} + y^{2}\) è dispari, \(p\) deve essere necessariamente del tipo \(p=4k+1\).
Dimostriamo ora che la condizione è anche sufficiente. Scegliamo un intero \(r\) tale che \(r^{2}\equiv -1 \pmod{p}\) e consideriamo il multiinsieme costituito dai numeri

\[ X=\{ar+b; 0 \le a,b \le \lfloor\sqrt{p}\rfloor \} \]

Notiamo che \(\sqrt{p}\) non è un intero. Il multiinsieme \(X\) contiene più di \(p\) elementi e quindi, per il principio dei cassetti di Dirichlet, esistono due coppie diverse \((a_{1},b_{1}), (a_{2},b_{2})\), con \(0 \le a_{1},b_{1},a_{2},b_{2} \le \lfloor\sqrt{p}\rfloor \), tali che

\[ a_{1}r + b_{1} \equiv a_{2}r + b_{2} \pmod{p} \]

Se indichiamo \(x=a_{2}-a_{1}\) e \(y=b_{2}-b_{1}\) abbiamo

\[ y^{2} \equiv x^{2}r^{2} \equiv – x^{2} \pmod{p} \]

Quindi \(p|x^{2}+y^{2}\). Notiamo ora che essendo \(p\) primo si ha \(\lfloor\sqrt{p}\rfloor \lt \sqrt{p}\). Quindi poiché \(0 < x^{2}+y^{2}<2 (\lfloor \sqrt{p}\rfloor)^{2}<2p\) allora deve essere \(p=x^{2}+y^{2}\).

Seconda dimostrazione
Diamo una seconda dimostrazione utilizzando gli interi di Gauss. Dal teorema 3.2 sappiamo che esiste un intero \(x\) tale che

\[ kp = x^{2}+1 = (x+i)(x-i) \ , \quad k,x \in \mathbb{Z} \]

Supponiamo ora che \(p\) sia irriducibile nell’anello \(\mathbb{Z}[i]\). Allora è anche un primo di Gauss e quindi deve essere \(p|(x+i)\) oppure \(p|(x-i)\). Ma questo non è possibile in quanto l’elemento \(\dfrac{x+i}{p}=\dfrac{x}{p}+ \dfrac{i}{p}\) non è un intero di Gauss. Quindi \(p\) non è irriducibile e si fattorizza in modo non banale in due interi di Gauss che non sono delle unità:

\[ p =(a+bi)(c+di) \]

con \( N(a+bi) \gt 1\) e \(N(c+di) \gt 1\). Quindi abbiamo

\[ N(p)=p^{2} =(a^{2}+b^{2})(c^{2}+d^{2}) \]

Questa è una equazione nell’anello degli interi ordinari. Poiché i due interi di Gauss non sono delle unità, l’unica soluzione possibile è

\[ p=N(a+bi)= a^{2}+b^{2} \]

Ne deriva anche che deve essere \(c+di=a-bi\).

Per una altra dimostrazione interessante proposta da Don Zagier vedere ^[2].

Nota
Per la sua dimostrazione Eulero utilizzò il cosiddetto metodo della discesa infinita (infinite descent). Si tratta di un metodo di dimostrazione per assurdo basato sul fatto che i numeri naturali minori di un dato numero naturale \(n\) sono un insieme finito. Di fatto è logicamente equivalente al più noto principio di induzione matematica. Per studiare la dimostrazione originale di Eulero vedere ^[5].

3.2) Numeri composti somma di due quadrati

Teorema 3.4
Se \(p=4k+3\) e \(p|n\), allora \(n\) non ha alcuna rappresentazione primitiva come somma di due quadrati.

Dimostrazione
Supponiamo che esista una rappresentazione primitiva:

\[ p|(a^{2}+b^{2}) \ , \quad (a,b)=1 \]

L’equazione diofantea \(b=ax \pmod{p}\) ammette una soluzione, in quanto \(p \nmid a\) e \(p \nmid b\). Quindi esiste un \(t\) tale che

\[ a^{2}(1+t^{2})= a^{2}+b^{2} \equiv 0 \pmod{p} \]

Poiché \((a,p)=1\) ne segue che

\[ 1 + t^{2} \equiv 0 \pmod{p} \]

Ma questo è impossibile in quanto sappiamo che \( \left(\frac{-1}{p}\right)=(-1)^{\frac{p-1}{2}}\), e quindi se \(p=4k+3\) il numero \(-1\) non è un residuo quadratico modulo \(p\).

Ricordiamo che il simbolo \(p^{k}||n\) indica che \(k\) è la massima potenza di \(p\) che divide \(n\), cioè \(p^{k}|n\) ma \(p^{k+1}\nmid n\). Ad esempio \(2^{2} ||12\) e \(3^{2}||54\).

Dal teorema precedente deriva subito il seguente:

Teorema 3.5
Sia \(p=4k+3\) un numero primo. Se \(p^{r}||n\) e r è dispari, allora \(n\) non è rappresentabile come somma di quadrati.

Nel caso di un numero composto, le condizioni per poter rappresentare un intero come somma di due quadrati sono contenute nel seguente teorema di Fermat:

Teorema 3.6 – Fermat
Sia dato un intero positivo \(n\) con la seguente scomposizione in fattori primi:

\[n = 2^{t}\prod_{i}p_{i}^{r_{i}} \prod_{j}q_{j}^{s_{j}} \]

dove \(p_{i} \equiv 1 \pmod{4}\) e \(q_{j} \equiv 3 \pmod{4}\). Allora è possibile scrivere \(n=x^{2}+ y^{2}\) se e solo se tutti gli esponenti \(s_{j}\) sono pari.

Per una dimostrazione vedere uno dei testi della bibliografia.

3.3) Interi somma di due quadrati non nulli

Il teorema di Fermat non esclude che uno dei due addendi della somma di quadrati sia nullo. Ad esempio \(9 = 3^{2}+0^{2}\). Ci si può chiedere cosa cambia se imponiamo che entrambi i quadrati siano non nulli.
Ricordiamo soltanto i seguenti risultati:

Teorema 3.7
Sia \(n \gt 1\) un intero. Allora esistono due interi \(a,b \in \mathbb{Z}\) con \((a,b)=1\) tali che \(n=a^{2}+b^{2}\) se e solo se \(-1\) è un residuo quadratico modulo \(n\), cioè \(\left(\dfrac{-1}{n}\right)=1\).

Teorema 3.8
Un intero \(n\) può essere scritto come somma di due quadrati non nulli se e solo se tutti i suoi fattori primi della forma \(q \equiv 3 \ \pmod 4\) hanno esponenti pari, e, se \(n\) è un quadrato perfetto, allora deve essere divisibile da qualche numero primo \(p \equiv 1 \pmod {4}\).

Esercizio 3.2
Verificare quali dei seguenti numeri possono essere rappresentati come somma di due quadrati non nulli:

\[ \begin{array}{l} 45,10,25,100 \\ 36,81,144,400,10000 \\ \end{array} \]

---

4) La funzione aritmetica \(r(n)\)

Definiamo la funzione aritmetica \(r(n)\) come il numero delle rappresentazioni di \(n\) nella forma

\[ n=x^{2}+y^{2} \ , \quad x,y \in \mathbb{Z} \]

Tale funzione viene anche indicata con il simbolo \(r_{2}(n)\).
Come abbiamo detto in precedenza, si contano come diverse le rappresentazioni che differiscono per i segni o per l’ordine, ed è ammesso anche lo zero. Alcuni esempi sono i seguenti:

\[ \begin{array}{l} 0 = 0^{2} +0^{2} \implies r(0)=1 \\ 1 = (\pm 1)^{2}+ 0^{2}=0^{2} + (\pm 1)^{2} \implies r(1)=4 \\ 2= (\pm 1)^{2}+ (\pm 1)^{2} \implies r(2)=4 \end{array} \]

Dai teoremi dimostrati nel paragrafo precedente abbiamo il seguente risultato parziale:

Teorema 4.1
Se \(p\) è un primo del tipo \(4k+1\) allora \(r(p)=8\). La rappresentazione è di fatto unica; le altre sono diverse solo per l’ordine e per i segni.
Se \(n\) è un intero positivo del tipo \(4k+3\) allora \(r(n)=0\).

Sia \(n=p_{1}^{a_{1}} \cdots p_{k}^{a_{k}}\) la fattorizzazione di un intero positivo. Ricordiamo che il numero dei divisori di \(n\), indicato con \(d(n)\), è dato dalla seguente formula

\[ d(n)=(a_{1}+1) \cdots (a_{k}+1)=\prod\limits_{i=1}^{k}(a_{i}+1) \]

Il seguente teorema è stato dimostrato da Carl Gustav Jacobi (1804-1851), uno dei più grandi matematici del secolo XIX. Uno dei suoi maggiori contributi è la teoria delle funzioni ellittiche e delle funzioni theta, sviluppata nella sua importante opera ‘Fundamenta nova theoriae functionum ellipticarum‘, pubblicata in latino nel \(1829\). Una forma sostanzialmente equivalente del teorema era stata dimostrata anche da Gauss nella sua opera fondamentale ‘Disquisitiones Arithmeticae’, pubblicata nel \(1801\) in latino.

Teorema 4.2 – Jacobi-Gauss

\[ r(n)=4(d_{1}(n) – d_{3}(n)) \]

dove \(d_{1}(n),d_{3}(n)\) sono rispettivamente il numero di divisori di \(n\) della forma \(4k+1\) e \(4k+3\).

Dimostrazione
Seguiamo la dimostrazione dal libro di Hardy-Wright. Poniamo

\[ n = A^{2}+ B^{2}=2^{\alpha} n_{1}n_{2} \] \[ \begin{array}{l} n_{1}=\prod\limits_{p \equiv 1 \pmod{4}}p^{r} \\ n_{2}= \prod\limits_{q \equiv 3 \pmod{4}}q^{s} \end{array} \]

Utilizzando la teoria degli interi di Gauss possiamo scrivere la seguente fattorizzazione

\[ n = \{(1+i)(1-i)\}^{\alpha}\prod\limits_{}\{(a+bi)(a-bi)\}^{r} \prod\limits_{}q^{s} \]

Gli interi di Gauss \(1 \pm i,a \pm bi, q\) sono primi nell’anello \(\mathbb{Z}[i]\). Ogni primo \(p\) essendo del tipo \(4k+1\) è somma di quadrati: \(p=a^{2}+b^{2}\). Gli interi \(a,b\) sono positivi e diversi tra loro. Per ipotesi

\[ n=A^{2}+B^{2}=(A+Bi)(A-Bi) \]

e quindi possiamo scrivere

\[ \begin{array}{l} A+Bi=i^{t}(1+i)^{\alpha_{1}}(1-i)^{\alpha_{2}}\prod\limits_{}\{(a+bi)^{r_{1}}(a-bi)^{r_{2}}\} \prod\limits_{}q^{s_{1}} \\ A-Bi=i^{-t}(1-i)^{\alpha_{1}}(1+i)^{\alpha_{2}}\prod\limits_{}\{(a-bi)^{r_{1}}(a+bi)^{r_{2}}\} \prod\limits_{}q^{s_{2}} \\ \end{array} \]

dove \(t=0,1,2,3, \quad \alpha_{1}+\alpha_{2}=\alpha, \quad r_{1}+r_{2}=r\). Inoltre \(s\) deve essere pari e \(s_{1}=s_{2}=\dfrac{s}{2}\).
Ne deduciamo che \(n_{2}=\prod\limits_{q}q^{2s_{1}}\) è un quadrato. I fattori \(q\) sono quindi equamente divisi fra \(A+Bi\) e \(A-Bi\).
Per gli altri fattori il numero delle possibili scelte sembrerebbe essere

\[ 4 (\alpha+1) \prod\limits_{}(r+1) \]

Tuttavia, l’intero di Gauss \(\frac{1-i}{1+i}=-i\) è un’unità e quindi una modifica negli esponenti \(\alpha_{1},\alpha_{2}\) non produce alcuna variazione rispetto a quella prodotta dall’esponente \(t\). Quindi il numero effettivo delle possibili scelte che possono produrre variazioni in \(A\) e in \(B\) è

\[ 4 \prod\limits_{}(r+1)=4d(n_{1}) \]

dove \(d(n_{1})\) indica il numero dei divisori di \(n_{1}\).
Il numero delle diverse possibili rappresentazioni di \(n\) come somma di quadrati corrisponde ai diversi valori di \(A,B\) che possiamo scegliere. Tenendo conto del teorema fondamentale dell’aritmetica nell’anello \(\mathbb{Z}[i]\), si trova che tale numero è dato dai diversi valori degli esponenti \(t,r_{1},r_{2}\). Ci sono quindi \(4d(n_{1})\) differenti insiemi di valori possibili per i numeri \(A,B\).
Questo completa la dimostrazione. Infatti basta osservare che vale la seguente relazione

\[ d(n_{1})=d_{1}(n) -d_{3}(n) \]

Se \(n=2^{\alpha}n_{1}n_{2}\) il fattore \(2^{\alpha}\) non influisce sul calcolo di \(d_{1}(n) -d_{3}(n)\). Inoltre i divisori di \(n_{1}n_{2}\) sono i termini del prodotto

\[ \prod\limits_{}(1+p+ \cdots + p^{r})\prod\limits_{}(1+q+ \cdots + q^{s}) \]

Un divisore è del tipo \(4k+1\) se contiene un numero pari di fattori \(q\), altrimenti è del tipo \(4k+3\). La differenza \(d_{1}(n)-d_{3}(n)\) è quindi uguale a zero se almeno un esponente \(s\) è dispari, altrimenti è uguale a \(d(n_{1})\).

4.1) La funzione theta di Jacobi

Il teorema 4.2 è stato inizialmente dimostrato da Jacobi mediante la sua teoria delle funzioni ellittiche e delle funzioni theta.

Definizione 4.1 – La funzione theta di Jacobi

\[ \theta(x)= 1+ 2x + 2x^{4}+ 2x^{9}+ \cdots = \sum\limits_{n=-\infty}^{\infty}x^{n^{2}} \]

Partendo da questa definizione calcoliamo il quadrato

\[ \theta^{2}(x)= \left( 1+ 2x + 2x^{4}+ 2x^{9}+ \cdots \right)^{2} \]

Notiamo che nello sviluppo di \(\theta^{2}(x)\) il coefficiente di \(x^{n}\) è proprio \(r_{2}(n)\), in quanto ogni coppia \((a,b)\) tale che \(a^{2}+b^{2}=n\) contribuisce con un valore unitario. Quindi vale il seguente teorema:

Teorema 4.3

\[ \theta^{2}(x)= \left(\sum\limits_{n=-\infty}^{\infty}x^{n^{2}}\right) \cdot \left(\sum\limits_{m=-\infty}^{\infty}x^{m^{2}}\right)= \\ \sum\limits_{(n,m) \in \mathbb{Z}\times \mathbb{Z}}^{\infty}x^{n^{2}+m^{2}}=\sum\limits_{n=0}^{\infty}r(n)x^{n} \]

Jacobi ha dimostrato la seguente identità:

Teorema 4.4 – Jacobi

\[ \theta^{2}(x)= 1+ 4\left(\frac{x}{1-x}- \frac{x^{3}}{1-x^{3}} + \frac{x^{5}}{1-x^{5}} – \frac{x^{7}}{1-x^{7}}+ \cdots\right) \]

Mediante l’identità di Jacobi possiamo dare un’altra dimostrazione della formula per la funzione \(r_{2}(n)\).

Teorema 4.5

\[ r_{2}(n) = 4 \sum\limits_{d \text{ dispari} \\ d|n} (-1)^{\dfrac{d-1}{2}} \]

Dimostrazione
Ricordando lo sviluppo della serie geometrica

\[ \frac{1}{1-x^{n}}=1+ x^{n}+ x^{2n}+ \cdots \]

e utilizzando i teoremi 4.3 e 4.4 troviamo facilmente

\[ \theta^{2}(x)= 1 + 4 \sum\limits_{n=1}^{\infty} \left(\frac{x^{4n-3}}{1- x^{4n-3}} -\frac{x^{4n-1}}{1- x^{4n-1}}\right) = \\ 1 + 4 \sum\limits_{m=1}^{\infty} \left(\sum\limits_{r=1}^{\infty}x^{(4m-3)r} -\sum\limits_{r=1}^{\infty}x^{(4m-1)r}\right) = \\ 1 + 4 \sum\limits_{n=1}^{\infty} \left(\sum\limits_{\substack{d|n\\ d \equiv 1 \pmod{4}}} 1 -\sum\limits_{\substack{d|n \\ d \equiv 3 \pmod{4}}}1\right)x^{n} \\ \]

Uguagliando i coefficienti di \(x^{n}\) abbiamo

\[ r_{2}(n)=4(d_{1}(n) – d_{3}(n)) \]

Le funzioni theta hanno una grande importanza nello studio delle funzioni ellittiche e degli integrali ellittici. Le proprietà delle funzioni theta sono caratterizzate da un grande bellezza e hanno applicazioni non solo nella teoria dei numeri, ma in varie branche della matematica pura e applicata. Per una introduzione vedere il libretto di Bellman ^[7].

---

5) Il metodo di fattorizzazione di Eulero

Supponiamo di voler fattorizzare un intero positivo \(x\) nel prodotto di due interi. Possiamo supporre \(x\) dispari senza perdere generalità. Supponiamo di conoscere due diverse rappresentazioni di \(n\) come somma di due quadrati:

\[ x = a^{2}+b^{2}=c^{2}+d^{2} \]

Poiché \(x\) è dispari, possiamo supporre \(a,c\) dispari e \(b,d\) pari. Scomponiamo in fattori mediante i prodotti notevoli

\[ (a-c)(a+c)=(d-b)(d+b) \]

Sia \((a-c,d-b)=k\); allora

\[ \begin{array}{l} a-c = kl \\ d-b= km \\ (l,m)=1 \\ \end{array} \]

Notiamo che \(k\) è un numero pari, poiché \(a-c\) e \(d-b\) sono pari.
Eliminando \(k\) e sostituendo nell’equazione precedente troviamo

\[ l(a+c)=m(d+b) \]

Poiché \((l,m)=1\) allora \(m\) deve dividere \(a+c\) e quindi

\[ a+c=mn \]

per un certo intero \(n\). Sostituendo nell’equazione precedente abbiamo

\[ d+b=ln \]

Dalle espressioni precedenti deriva che \(n=(a+c,d+b)\) e quindi \(n\) è pari, essendo \(a,c\) dispari e \(b,d\) pari. Ora con un facile calcolo abbiamo

\[ x =\frac{(a-c)^{2}+(a+c)^{2}+(d-b)^{2}+(d+b)^{2}}{4} \]

Eliminando le variabili \(a,b,c,d\) nelle espressioni precedenti otteniamo la fattorizzazione dell’intero \(x\):

\[ x =\left[\left(\frac{k}{2}\right)^{2}+\left(\frac{n}{2}\right)^{2}\right](m^{2}+l^{2}) \]

Esempio 5.1
Con il metodo di Eulero fattorizzare i seguenti numeri:

\[ \begin{array}{l} 221 = 5^{2}+14^{2}=10^{2}+11^{2} \\ 493 = 22^{2}+3^{2}=18^{2}+13^{2} \\ \end{array} \]

---

Conclusione

Il problema della somma di due quadrati può essere esteso al caso di \(3,4\) quadrati. Legendre ha dimostrato che un intero può essere espresso come somma di \(3\) quadrati se e solo se non è della forma \(4^{k}(8n+7)\), con \(k,n \ge 0\) .
Nel \(1770\) Lagrange ha dimostrato che ogni intero può essere espresso come somma di \(4\) quadrati.
Waring nel \(1770\) formulò la congettura che ogni intero positivo è somma di \(9\) cubi positivi o nulli, e anche che ogni intero positivo è somma di \(19\) quarte potenze. In generale, congetturò che per ogni intero positivo \(k\) esiste un intero positivo \(g(k)\) tale che ogni intero positivo è somma di \(g(k)\) potenze con esponente \(k\). La congettura di Waring è stata dimostrata nel \(1909\) da Hilbert.
In articoli successivi studieremo il teorema di Lagrange e il problema generale di Waring.

---

Bibliografia

^[1]F. Jarvis – Algebraic Number Theory (Springer)

^[2]M. Aigner – Proofs from THE BOOK (Springer)

^[3]T. Apostol – Modular Functions and Dirichlet Series in Number Theory (Springer)

^[4]Niven, Zuckerman, Montgomery – An introduction to the Theory of Numbers (Wiley)

^[5]http://nonagon.org/ExLibris/euler-proves-fermats-theorem-sum-two-squares

^[6]C. G. Jacobi – Fundamenta nova theoriae functionum ellipticarum (Cambridge U.P.)

^[7]R. Bellman – A Brief Introduction to Theta Functions (Dover)