Introduzione alla Trigonometria – La Misura degli Angoli e le Funzioni Trigonometriche

La trigonometria può essere considerata come una branca della geometria. La parola “geometria” deriva dal greco, come unione delle due parole “geo” (terra) e “metron” (misura). Riguarda lo studio delle proprietà e delle relazioni dei punti, delle linee, degli angoli, delle superfici piane e dei solidi. Gli ‘Elementi’ di Euclide costituiscono il testo base della geometria. Quest’opera, composta da \(13\) libri, è il testo matematico più diffuso nella storia. Contiene i risultati fondamentali della matematica del mondo antico: teoria dei numeri, algebra, teoria delle proporzioni, geometria piana e solida, metodi per il calcolo delle aree e dei volumi.
Nell’opera di Euclide la geometria viene sviluppata con il metodo assiomatico: a partire da concetti primitivi, postulati ed assiomi vengono dimostrati numerosi teoremi, tramite il metodo deduttivo della logica matematica.
La parola trigonometria deriva dalla parole greche trigonon (tre angoli) e metron (misura). La trigonometria studia le relazioni fra i lati e gli angoli di un triangolo. Per esprimere queste relazioni vengono introdotte le funzioni trigonometriche (seno, coseno, tangente, ecc.) che vedremo in seguito.
Molte proprietà, che negli Elementi di Euclide vengono espresse in modo puramente geometrico, possono essere anche formulate nel linguaggio della trigonometria.

1) Breve storia della trigonometria

In questo articolo considereremo esclusivamente la trigonometria piana, che studia gli angoli dei triangoli e dei poligoni piani. Ricordiamo che esiste anche la trigonometria sferica, che viene utilizzata per studiare gli angoli su una sfera, ed è importante in astronomia e nella navigazione. Infatti storicamente la trigonometria è nata come ausilio agli astronomi Babilonesi, Egizi e Greci, per misurare le grandezze degli angoli e degli archi di circonferenza. A quel tempo la Terra veniva considerata al centro della sfera celeste. Per calcolare la posizione delle stelle e dei pianeti era necessario studiare la geometria dei triangoli sferici, cioè di triangoli i cui lati sono archi che stanno sulla superficie della sfera.
Il padre della trigonometria viene considerato l’astronomo greco Ipparco (190 – 120 a.C.). Ipparco introdusse il sistema sessagesimale, inventato dai Babilonesi, per misurare gli angoli mediante gradi, minuti e secondi. La posizione di un oggetto celeste veniva espressa mediante le coordinate astronomiche ascensione retta e declinazione (vedi Treccani).
Ipparco e in seguito Tolomeo (100 d.C. circa – 170 d.C. circa) pubblicarono delle tabelle con i valori degli angoli corrispondenti a varie corde su un cerchio.

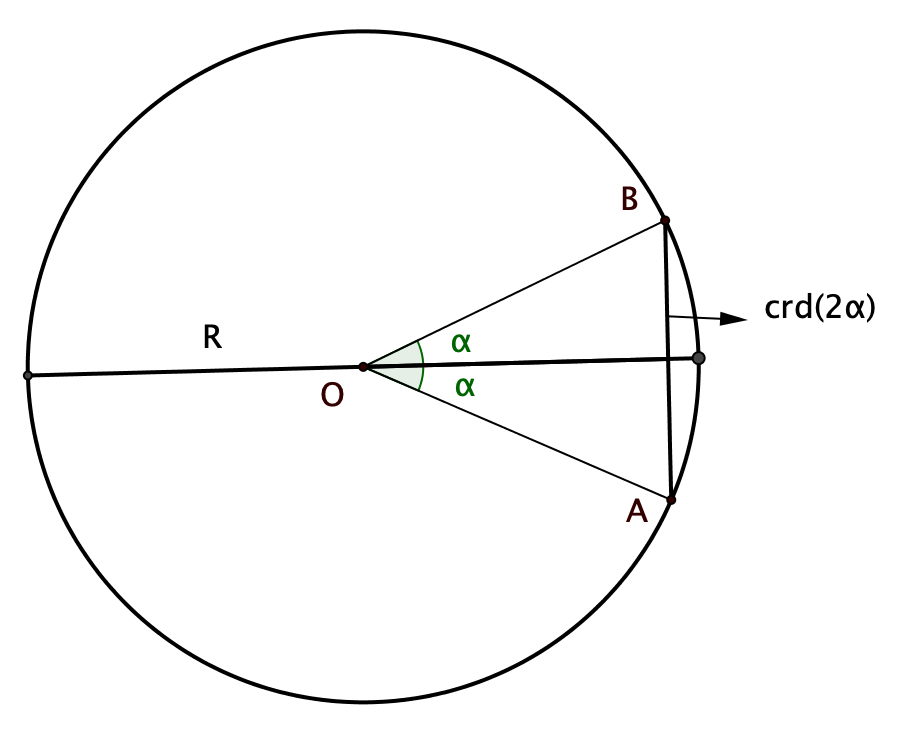
La formula per calcolare la lunghezza di una corda che sottende un dato arco di circonferenza di raggio \(R\) è la seguente:

\[ \text{crd}(2\alpha)= 2R \sin \alpha \]

Le tavole di Ipparco e Tolomeo vennero riprese e ampliate dai matematici indiani e arabi. La traduzione in latino delle opere degli Arabi contiene la parola sinus. L’utilizzo del termine sinus venne favorito dal matematico Leonardo Pisano (1170-1242 circa), detto il Fibonacci.
La parola “trigonometria” apparve per la prima volta nel libro del matematico e teologo tedesco Bartholomeo Pitiscus (1561-1613). Il titolo del libro, pubblicato nel \(1595\), è ‘Trigonometria, sive de solutione triangulorum tractatus brevis et perspicuus’.
Con Eulero (1707-1783) la trigonometria divenne una branca autonoma della matematica, separata dall’astronomia. Nella sua opera fondamentale ‘Introductio in analysin infinitorum’ (1748) Eulero presenta le principali proprietà delle grandezze trigonometriche, come il seno e il coseno, considerate ora come funzioni piuttosto che come misure di grandezze geometriche.
Per un approfondimento completo sulla storia della trigonometria vedere il testo di Brummelen ^[1].

2) La misura degli angoli

Nella geometria piana euclidea l’angolo è definito come una delle due parti di piano individuate da due semirette aventi l’origine in comune. L’angolo \(\angle AOB\) nella figura sottostante è generato dalla semiretta \(\overline{OA}\) che ruota nel piano fino a raggiungere la posizione finale \(\overline{OB}\). La posizione iniziale \(\overline{OA}\) si chiama lato iniziale dell’angolo, mentre la posizione finale \(\overline{OB}\) si chiama lato finale dell’angolo. L’angolo si considera positivo se la rotazione è antioraria, altrimenti è negativo.

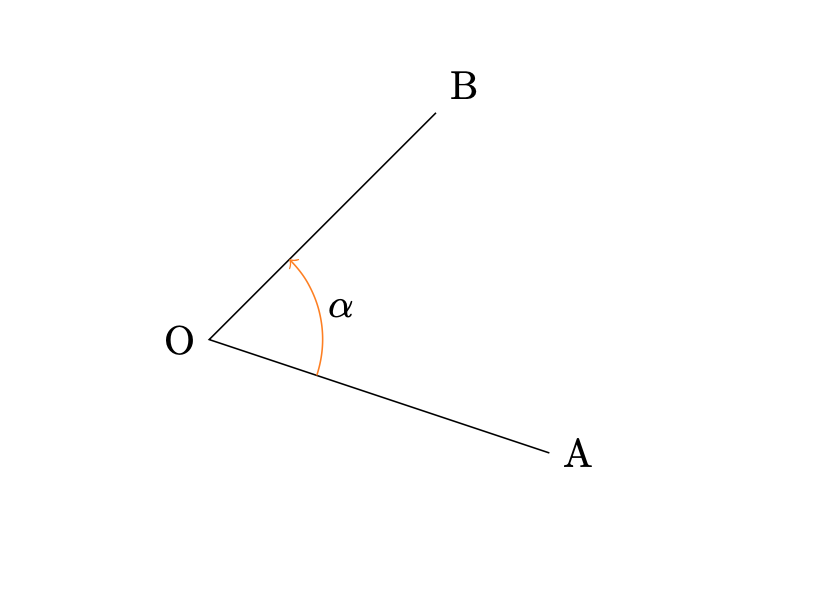
Se la rotazione è uguale ad un quarto di un giro completo l’angolo si dice retto.

2.1) La misura degli angoli in gradi – Il sistema sessagesimale

È noto che se conosciamo le lunghezze dei lati di un triangolo, allora sono determinati in modo univoco anche gli angoli. Un teorema della geometria euclidea afferma che la somma dei tre angoli di ogni triangolo è uguale al doppio di un angolo retto. Tuttavia tranne che in casi particolari (ad esempio un triangolo equilatero) non è semplice determinare la misura degli angoli.
In primo luogo è necessario stabilire una unità di misura per gli angoli, così come viene fatto con le lunghezze. Una unità pratica di misura per gli angoli è il grado. Un angolo che consiste in una rotazione antioraria completa viene definito uguale a \(360\) gradi, o \(360^{\circ}\), e viene chiamato angolo giro. La metà di una rotazione completa è un angolo piatto, che misura \(180\) gradi. Infine un quarto di rotazione completa è un angolo retto di \(90\) gradi. Nel caso servano misure più accurate, vengono utilizzati anche i minuti e i secondi:

\[ \begin{array}{l} 1 \text{ grado} = 60 \text{ minuti}\\ 1 \text{ minuto} = 60 \text{ secondi} \end{array} \]

Ad esempio un angolo \(\alpha\) che misura \(70\) gradi, \(20\) minuti e \(15\) secondi viene indicato con la simbologia \(\alpha = 70^{\circ} 20′ 15″\).
Dalla definizione segue che un angolo può avere una misura qualsiasi, negativa (se rotazione oraria) o positiva (se rotazione antioraria). Ad esempio \(10\) rotazioni complete in senso antiorario corrispondono ad un angolo di \(3600\) gradi.

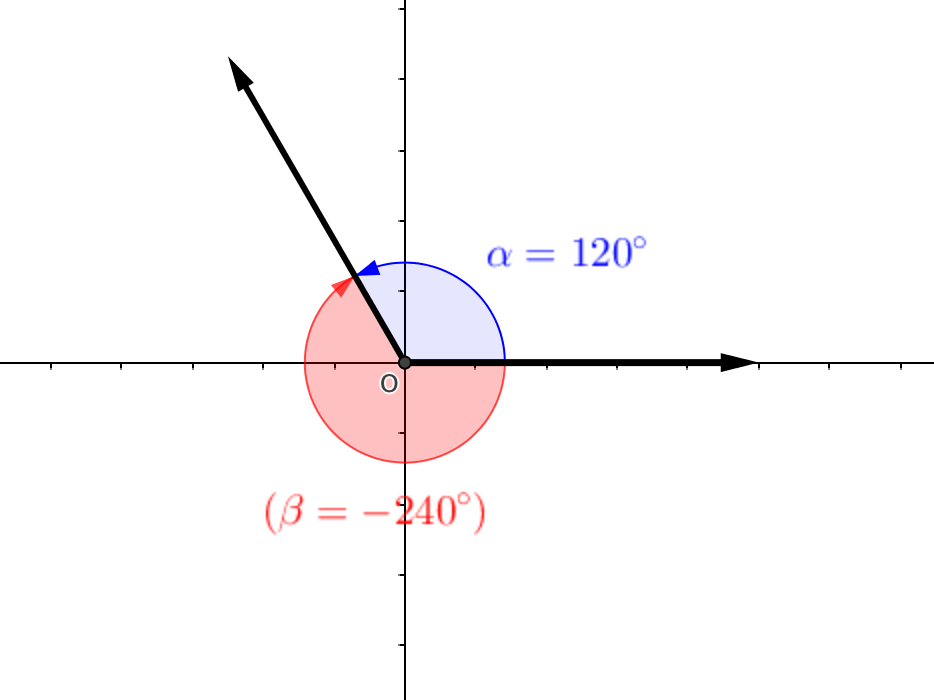
La scelta del valore \(360\) per una rotazione completa probabilmente è dovuta agli astronomi babilonesi, i quali calcolavano in \(360\) giorni il periodo necessario per l’apparente rivoluzione completa del Sole intorno alla Terra.
Un’altra spiegazione possibile è di natura matematica: il numero \(360\) ha molti divisori, precisamente \(24\). Questo fatto è utile quando si devono fare calcoli manuali.
La trigonometria degli astronomi babilonesi si basava sulla misura delle corde del cerchio. In particolare una corda di lunghezza uguale al raggio era considerata \(\dfrac{1}{6}\) della lunghezza della circonferenza, assumendo quindi un valore \(\pi = 3\). In alcune tavole dei Babilonesi dei secoli successivi si assumeva un valore più preciso, cioè \(\pi \approx 3,125\), molto vicino al valore corretto.

Esercizio 2.1
Determinare i \(24\) divisori del numero \(360\).

Il sistema centesimale
Nel \(1795\), dopo la Rivoluzione francese, venne proposto in Francia il sistema centesimale. In questo sistema un angolo retto viene diviso in \(100\) parti chiamati gradi, quindi un angolo giro contiene \(400\) gradi. Ogni grado a sua volta è suddiviso in \(100\) parti chiamati minuti, e ogni minuto è suddiviso in \(100\) parti chiamati secondi. Nonostante i suoi meriti questo sistema non ha avuto diffusione, anche perché ormai il sistema sessagesimale era ampiamente utilizzato, e sarebbe stato necessario un lavoro dispendioso per ricalcolare molte tavole.

2.2) La misura in radianti

Il radiante costituisce un’altra fondamentale unità per la misura degli angoli. E’ una misura assoluta che non dipende da un valore arbitrario scelto come valore unitario. Per questo viene utilizzata in preferenza nella matematica e nelle scienze esatte. Si tratta di una misura che deriva direttamente dalla geometria del cerchio. Consideriamo la figura seguente:

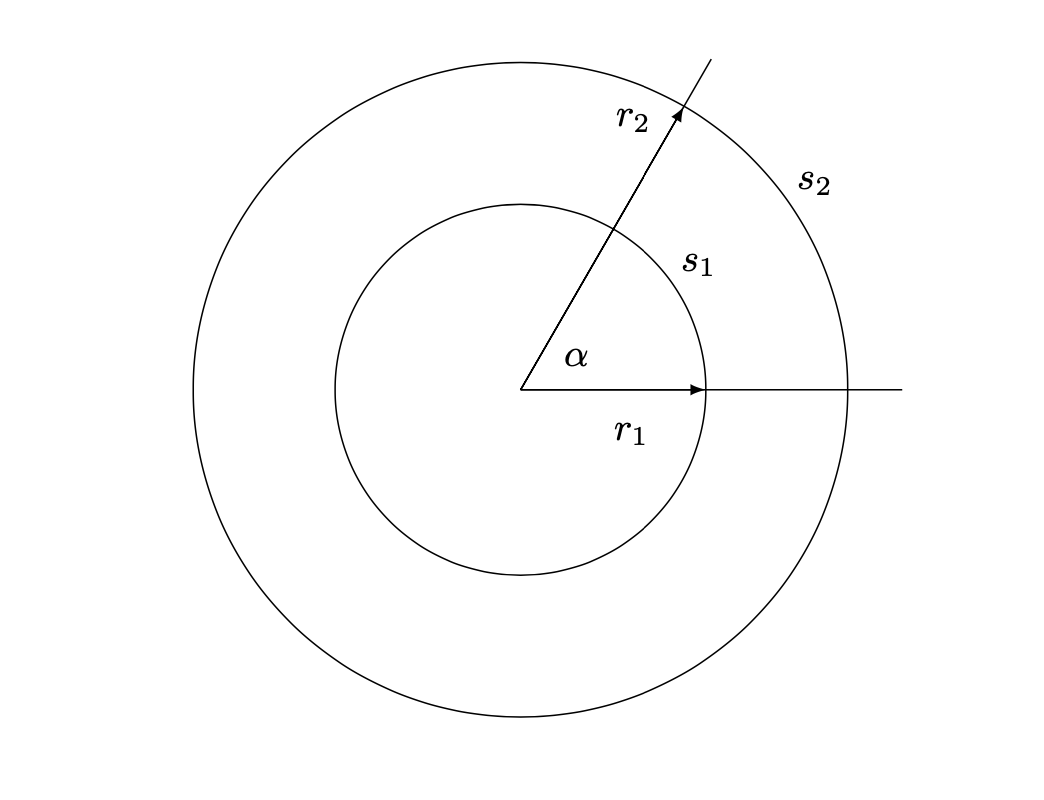
Definizione 2.1
La misura in radianti di un angolo è uguale al rapporto fra la lunghezza dell’arco di circonferenza che sottende l’angolo e il raggio del cerchio:

\[ \alpha = \frac{s}{r} \]

La misura in radianti di un angolo retto è quindi uguale a \(\dfrac{\pi}{2}\).

Esercizio 2.2
Dimostrare che questa definizione è indipendente dalla grandezza del cerchio. Cioè, dati due cerchi di raggi \(r_{1},r_{2}\) (vedi figura 2.1) si ha:

\[ \frac{s_{1}}{r_{1}}= \frac{s_{2}}{r_{2}} \]

La seguente tabella contiene la misura in radianti di alcuni angoli:

\[ \begin{array}{|c|c|} \hline \text{ gradi} & \text{ radianti} \\ \hline 30 & \dfrac{\pi}{6} \approx 0,5235988 \\ \hline 60 & \dfrac{\pi}{3} \approx 1,0471976 \\ \hline 90 & \dfrac{\pi}{2} \approx 1,5707963 \\ \hline 180 & \pi \approx 3,1415927 \\ \hline 270 & \dfrac{3\pi}{2} \approx4,7123890 \\ \hline 360 & 2\pi \approx 6,2831853 \\ \hline \end{array} \]

Origine della misura in radianti
Il concetto della misura in radianti viene in genere attribuito al matematico Roger Cotes (1682-1716). Comunque l’idea di misurare gli angoli mediante la lunghezza dell’arco di circonferenza unitaria era già presente in altri matematici del secolo XVIII. All’angolo giro si sarebbe potuto assegnare il valore di \(1\) radiante, invece si preferì assegnare il valore \(2\pi\), cioè la lunghezza della circonferenza unitaria. Questa scelta permette di semplificare diverse equazioni, anche se ne complica altre.
La parola radiante appare per la prima volta nel \(1873\), in alcuni documenti di James Thomson, fratello del famoso scienziato Lord Kelvin.

2.3) Conversione fra gradi e radianti

La formula di conversione della misura in gradi \(\theta_{g}\) e radianti \(\theta_{r}\) di un angolo è data dalla seguente proporzione:

\[ \theta_{r}:\theta_{g}=2\pi:360 \]

Ad esempio abbiamo:

\[ \begin{array}{l} 1 \text{ rad} = \dfrac{180^{\circ}}{\pi} \approx 57,29578^{\circ} \\ 1^{\circ} = \dfrac{\pi}{180} \approx 0,0174533 \text{ rad} \\ \end{array} \]

Possiamo riassumere le seguenti regole:

• Conversione da radianti a gradi: moltiplicare il valore in radianti per il numero \(\dfrac{180}{\pi}\).
• Conversione da gradi a radianti: moltiplicare il valore in gradi per il numero \(\dfrac{\pi}{180}\).

Esercizio 2.3
Convertire \(2,5\) radianti in gradi, minuti e secondi.
Lo schema da seguire è il seguente:

\[ \begin{array}{l} 2,5 \cdot 57,29578 = 143,2395 \\ 0,2395 \cdot 60 = 14,3670 \\ 0,3670 \cdot 60 = 22,02 \end{array} \]

Il risultato finale è quindi \(2,5 \text{ rad}= 143^{\circ} 14′ 22″\).

Esercizio 2.4
Convertire \(40^{\circ} 36′ 30″ \) in radianti.
Lo schema da seguire è il seguente:

\[ \begin{array}{l} 40^{\circ} 36′ 30″ = 40 + \dfrac{36}{60}+ \dfrac{30}{3600} = 40,6083^{\circ} \\ 40,6083^{\circ} = 40,6083\cdot 0,0174533 =0,7087 \text{ rad} \end{array} \]

Il risultato finale è quindi \(40^{\circ} 36′ 30″= 0,7087 \text{ rad}\).

Esercizio 2.5
Dato un cerchio di raggio \(5 \text{ cm} \). Determinare la lunghezza dell’arco che sottende un angolo al centro di \(2\) radianti.
Soluzione: \([10 \text{ cm}]\)

Esercizio 2.6
Trasformare \(3,5 \) radianti in gradi, minuti e secondi.
Soluzione: \([200^{\circ} 32′ 6″]\)

Esercizio 2.7
Esprimere in radianti gli angoli di un triangolo equilatero e di un esagono regolare.

Esercizio 2.8
Gli angoli di un triangolo stanno in rapporto di \(2:3:5\). Determinare i valori degli angoli in radianti e in gradi.

Esercizio 2.9
Le due lancette di un orologio sono allineate alle ore \(12:00\). Determinare quanti sono gli altri istanti nei quali le lancette si sovrappongono nel giro di \(24\) ore.
Soluzione: \([22]\)

2.4) Alcune semplici applicazioni

Consideriamo la figura seguente:

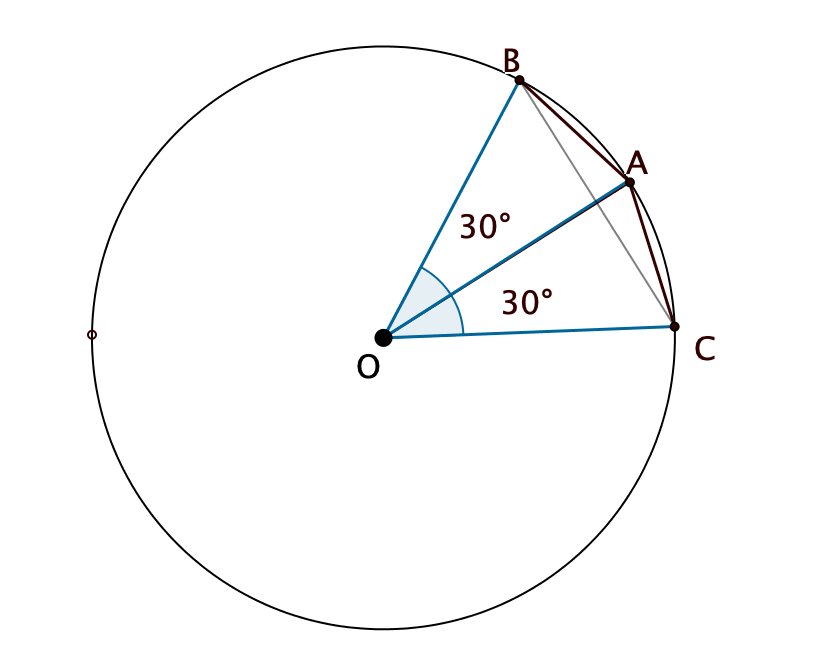
Un angolo \( 0 \le \theta \le 2\pi\) determina in modo univoco la lunghezza \(L\) dell’arco che lo sottende su una circonferenza di raggio \(R\) tramite la formula \(L = R \theta\), dove \(\theta\) è la misura in radianti. Anche la lunghezza della corda che sottende l’angolo è determinata in modo univoco. Ad esempio la corda \(\overline{AC}\) relativa all’angolo \(\angle AOC\).
In alcuni casi particolari si può calcolare la lunghezza della corda tramite gli strumenti della geometria elementare. Ad esempio se l’angolo è \(\dfrac{\pi}{2}\) allora tramite il teorema di Pitagora si trova la lunghezza della corda uguale a \(R\sqrt{2}\). In generale tuttavia bisogna ricorrere alle formule della trigonometria, come vedremo in seguito.
Un altro problema interessante è determinare come cambia la lunghezza della corda che sottende l’angolo, se si raddoppia l’angolo. L’arco corrispondente a \(60^{\circ}\) è il doppio dell’arco corrispondente a \(30^{\circ}\). Tuttavia non è immediato capire quanto è lunga la corda corrispondente all’angolo di \(60^{\circ}\), conoscendo la lunghezza della corda corrispondente all’angolo di \(30^{\circ}\). Dalla geometria sappiamo che è minore della somma delle corde associate ai due angoli di \(30^{\circ}\). Questo è dovuto al teorema di geometria secondo il quale in un triangolo un lato è minore della somma degli altri due. Per determinare la relazione precisa fra le la lunghezza delle corde è necessario utilizzare le formule della trigonometria.

Esercizio 2.10
Sia dato un cerchio di raggio \(R=2\). Determinare la lunghezza della corda corrispondente ad un angolo di \(90^{\circ}\).

Nel seguito, salvo indicazioni contrarie, gli angoli saranno sempre considerati misurati in radianti.

Esercizio 2.11 – Area del settore circolare
Dalla geometria elementare è noto che l’area di un settore circolare di lunghezza \(L\) è uguale a \(A=\dfrac{RL}{2}\). Basta applicare la proporzione:

\[ \pi R^{2}: 2\pi R= A : L \]

La lunghezza dell’arco è uguale a \(L=R\theta\), dove \(\theta\) è la misura in radianti dell’angolo sotteso dall’arco. Quindi

\[ \text{Area settore circolare}= \frac{R^{2} \theta}{2} \]

Esercizio 2.12
Calcolare l’area di un settore circolare relativo ad un angolo di \(30^{\circ}\) in un cerchio di raggio \(R=10\).

Esercizio 2.13
Calcolare la distanza percorsa da una ruota circolare di raggio \(50 \text{ cm}\), che compie \(2\) rotazioni complete senza strisciare.
Soluzione: \([\approx 628 \text{ cm}]\)

Ricordiamo che la velocità angolare \(\omega\) di un punto materiale che si muove su una circonferenza è definita come il rapporto fra l’angolo percorso e il tempo impiegato: \(\omega = \dfrac{\Delta \theta}{\Delta t}\). L’unità di misura della velocità angolare è data dal numero di radianti percorsi al secondo. La relazione tra la velocità lineare \(v\) e la velocità angolare \(\omega\) è \(v=R\omega\).

Esercizio 2.14
Una ruota gira con velocità angolare costante uguale a \(\dfrac{5 \pi}{3}\) radianti al secondo. Calcolare il numero di giri effettuati in un’ora.
Soluzione: \([ 3000 \text{ rotazioni in un’ora}]\)

Esercizio 2.15
Un settore circolare ha perimetro uguale a \(\dfrac{2}{3}\) della circonferenza di un cerchio di raggio \(R\). Determinare il valore in gradi dell’angolo del settore circolare.
Soluzione: \( [\approx 125^{\circ} 24′ 32″]\)

Esercizio 2.16
Determinare la velocità lineare di un punto che si trova all’equatore della Terra. Il raggio della Terra è circa \(6372 \text{ km}\). Supporre inoltre che la Terra compia una rotazione completa in \(24\) ore (in realtà il periodo è circa \(23 \text{ h}, 56 \text{ min}, 4 \text{ sec})\).
Soluzione: \([\approx 463,15 \text{ m/sec}]\)

Esercizio 2.17
A quale distanza un uomo alto \(2\) metri sottende un angolo di \(10^{\circ}\).

Esercizio 2.18
Due archi della stessa lunghezza su due cerchi diversi sottendono angoli di \(30^{\circ}\) e \(45^{\circ}\). Determinare il rapporto delle aree dei due cerchi.

Esercizio 2.19
Determinare la distanza dall’occhio al quale una moneta di \(2 \text{ cm}\) di diametro nasconde la Luna piena, il cui diametro angolare è \(31’\).

3) Le funzioni trigonometriche

3.1) Funzioni trigonometriche per angoli acuti

Definiamo inizialmente le funzioni trigonometriche di un angolo acuto \(0 \le \theta \le \dfrac{\pi}{2}\), mediante le proprietà dei triangoli rettangoli. La figura seguente illustra le definizioni delle funzioni seno, coseno e tangente.

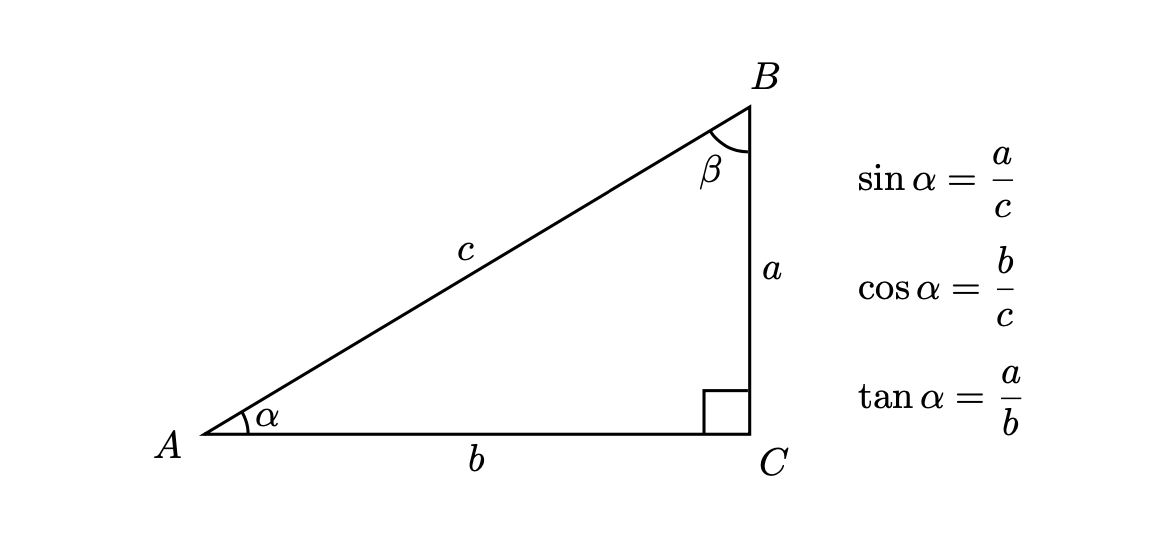
Come è noto due triangoli simili hanno gli angoli corrispondenti uguali e i lati corrispondenti in proporzione. In base al teorema di Talete, in due triangoli simili qualsiasi il rapporto fra coppie di lati corrispondenti è lo stesso. In particolare tutti i triangoli rettangoli che hanno lo stesso angolo acuto sono simili. Quindi la definizione data delle funzioni trigonometriche non dipende dalle dimensioni dei lati, ma solo dai rapporti fra di essi.
Le tre funzioni sopra descritte sono le più utilizzate. Sono definite anche queste altre tre seguenti funzioni:

\[ \begin{array}{l} \sec \alpha = \dfrac{1}{\cos \alpha} \quad \text{ (secante)} \\ \csc \alpha = \dfrac{1}{\sin \alpha} \quad \text{ (cosecante)} \\ \cot \alpha = \dfrac{1}{\tan \alpha} \quad \text{ (cotangente)} \\ \end{array} \]

Esercizio 3.1
Dimostrare le seguenti identità:

\[ \begin{array}{l} \sin^{2}\alpha+ \cos^{2}\alpha=1 \\ 1 + \tan^{2}\alpha = \dfrac{1}{\cos^{2}\alpha} \\ 1 + \cot^{2}\alpha = \dfrac{1}{\sin^{2}\alpha} \\ \end{array} \]

Come vedremo, queste relazioni dimostrate per gli angoli acuti valgono in generale, con l’eccezione degli angoli nei quali si annullano le funzioni seno e coseno.

Esercizio 3.2
Consideriamo la figura precedente. Indichiamo con \(\beta = \dfrac{\pi}{2}- \alpha\) l’angolo complementare di \(\alpha\). Verificare le seguenti relazoni:

\[ \begin{array}{l} \sin \beta = \cos \alpha \ ,\quad \cos \beta = \sin \alpha \\ \tan \beta = \cot \alpha \ ,\quad \cot \beta = \tan \alpha \\ \sec \beta = \csc \alpha \ ,\quad \csc \beta = \sec \alpha \end{array} \]

Esercizio 3.3
Sia dato un triangolo rettangolo i cui lati hanno lunghezze \(5,12,13\). Determinare i valori delle sei funzioni trigonometriche per l’angolo opposto al cateto minore del triangolo rettangolo.

3.2) Funzioni trigonometriche per angoli qualsiasi

La definizione data sopra ha delle limitazioni, in quanto considera soltanto angoli acuti di un triangolo rettangolo. Possiamo utilizzare il cerchio per estendere le definizioni ad angoli qualsiasi con valori dell’intervallo \(0 \le \theta \le 2\pi\).
Consideriamo un sistema di coordinate cartesiane ortogonali con origine \(O\) e un cerchio di raggio \(r\) con centro nell’origine. Sia dato un angolo \(\theta\) con vertice nell’origine, un lato coincidente con l’asse della ascisse e l’altro lato intersecante il cerchio in un punto \(P(x,y)\). Le tre funzioni trigonometriche sono definite mediante le coordinate cartesiane del punto di intersezione, come illustrato nella seguente figura:

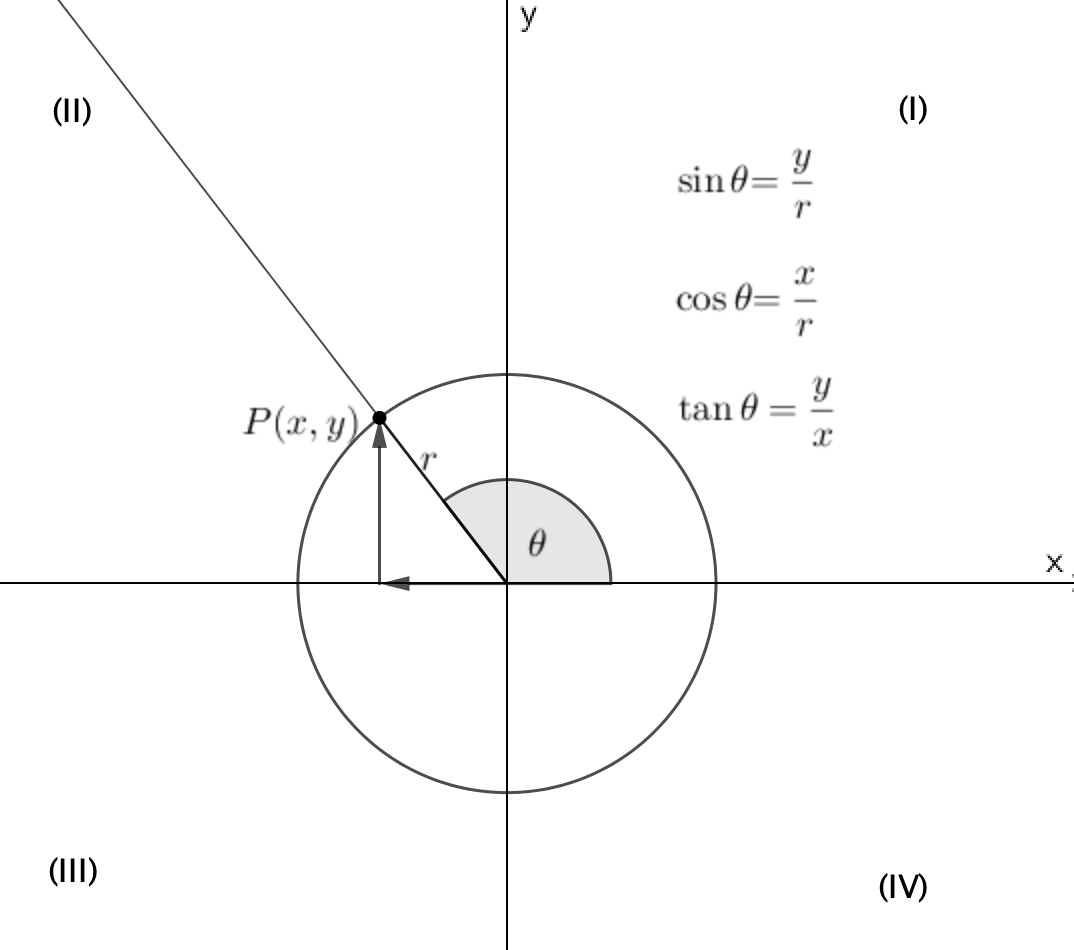
Nel caso dell’angolo acuto di un triangolo rettangolo i valori delle tre funzioni trigonometriche sono tutti positivi. Nel caso di angoli maggiori di un angolo retto vediamo che le funzioni trigonometriche assumono valori sia positivi sia negativi. Dividiamo il piano in quattro parti, chiamati i quadranti I,II,III,IV, iniziando da destra in alto e andando in senso antiorario. La seguente tabella descrive il valori dei segni nei quattro quadranti:

\[ \begin{array}{|c|c|c|c|} \hline \text{quadrante} & \text{seno} & \text{coseno} & \text{tangente} \\ \hline \text{I} & + & + & + \\ \hline \text{II} & + & – & – \\ \hline \text{III} & – & – & + \\ \hline \text{IV} & – & + & – \\ \hline \end{array} \]

Di seguito sono specificati i valori delle funzioni trigonometriche per alcuni angoli speciali:

\[ \begin{array}{|c|c|c|c|c|c|c|c|} \hline x & 0 & \dfrac{\pi}{6} &\dfrac{\pi}{4} &\dfrac{\pi}{3} &\dfrac{\pi}{2} &\pi &\dfrac{3\pi}{2} \\ \hline \sin x & 0 & \dfrac{1}{2} &\dfrac{\sqrt{2}}{2} &\dfrac{\sqrt{3}}{2} &1 &0 &-1 \\ \hline \cos x & 1 & \dfrac{\sqrt{3}}{2} &\dfrac{\sqrt{2}}{2} &\dfrac{1}{2} &0 &-1 &0 \\ \hline \tan x & 0 & \dfrac{\sqrt{3}}{3} &1 &\sqrt{3} &- &0 & – \\ \hline \end{array} \]

Come vediamo la tangente non è definita per angoli di \(90^{\circ}\) e \(270^{\circ}\), in quanto abbiamo una divisione per zero.

3.3) Estensione delle funzioni trigonometriche a tutti i valori reali

Ricordiamo che una funzione reale \(f(x)\) di una variabile reale \(x\), definita su un insieme di numeri reali \(A\), è una regola che ad ogni numero reale \(x \in A\) assegna un numero reale \(f(x)\). In simboli

\[ f : A \subset \mathbb{R} \to \mathbb{R} \]

L’insieme \(A\) viene chiamato il dominio della funzione. Può essere un sottoinsieme oppure coincidere con tutto l’insieme dei numeri reali \(\mathbb{R}\). L’insieme dei valori assunti dalla funzione, indicato con \(f(A)\), è il codominio.
In generale con il termine funzione si intende funzione ad un solo valore, in quanto ad ogni valore di \(x\) corrisponde un unico valore di \(y\). Se ad un valore di \(x\) corrispondono più valori di \(y\) allora parliamo di funzioni a più valori. In questo caso abbiamo una collezione di funzioni, ognuna delle quali viene chiamata determinazione della funzione a più valori. Per avere una funzione ad un solo valore in genere si sceglie una delle determinazioni, chiamata determinazione principale.
Una funzione \(f: A \to B\) si dice iniettiva se ogni elemento di B è associato al massimo a un solo elemento di A. In simboli

\[ x_{1} \neq x_{2} \implies f(x_{1}) \neq f(x_{2}) \]

Una funzione \(f: A \to B\) si dice suriettiva se ogni elemento di B è associato ad almeno  un  elemento di A. In simboli

\[ \forall y \in B \quad \exists x \in A : f(x)=y \]

Una funzione si dice biettiva, o biunivoca, se è sia iniettiva che suriettiva.
Una funzione si dice pari se \(f(-x)=f(x)\), si dice dispari se \(f(-x)=-f(x)\).
Una funzione si dice periodica se i valori assunti si ripetono ad intervalli regolari. Il periodo \(p\) della funzione è il più piccolo valore tale che

\[ f(x+p)=f(x) \]

Una volta definite le tre funzioni trigonometriche nell’intervallo \(0 \le \theta \le 2\pi\), possiamo definirle su tutti i valori reali tramite le seguenti relazioni:

\[ \begin{array}{l} \sin (\theta + 2\pi) = \sin \theta \\ \cos (\theta + 2\pi) = \cos \theta \\ \tan (\theta + \pi) = \tan \theta \\ \end{array} \]

Le formule precedenti mostrano che il seno e il coseno sono funzioni periodiche con periodo \(2\pi\), mentre la tangente ha periodo \(\pi\).
In modo simile possiamo estendere le funzioni secante, cosecante e cotangente.

Esempio 3.1

\[ \begin{array}{l} \sin (390^{\circ})= \sin 30^{\circ}= \dfrac{1}{2} \\ \cos (390^{\circ})= \cos 30^{\circ}= \dfrac{\sqrt{3}}{2} \\ \tan (390^{\circ})= \tan 30^{\circ}= \dfrac{1}{\sqrt{3}} \\ \end{array} \]

Possiamo quindi considerare le funzioni trigonometriche come funzioni di una variabile reale \(x\), dove la variabile \(x\) non è necessariamente la misura di un angolo in radianti.

Esercizio 3.4
Determinare il segno delle seguenti funzioni:

\[ \begin{array}{l} \sin (10000^{\circ}) \\ \cos (20000^{\circ}) \\ \tan (100000^{\circ}) \\ \sin (2000 \pi) \end{array} \]

4) Grafici delle funzioni trigonometriche

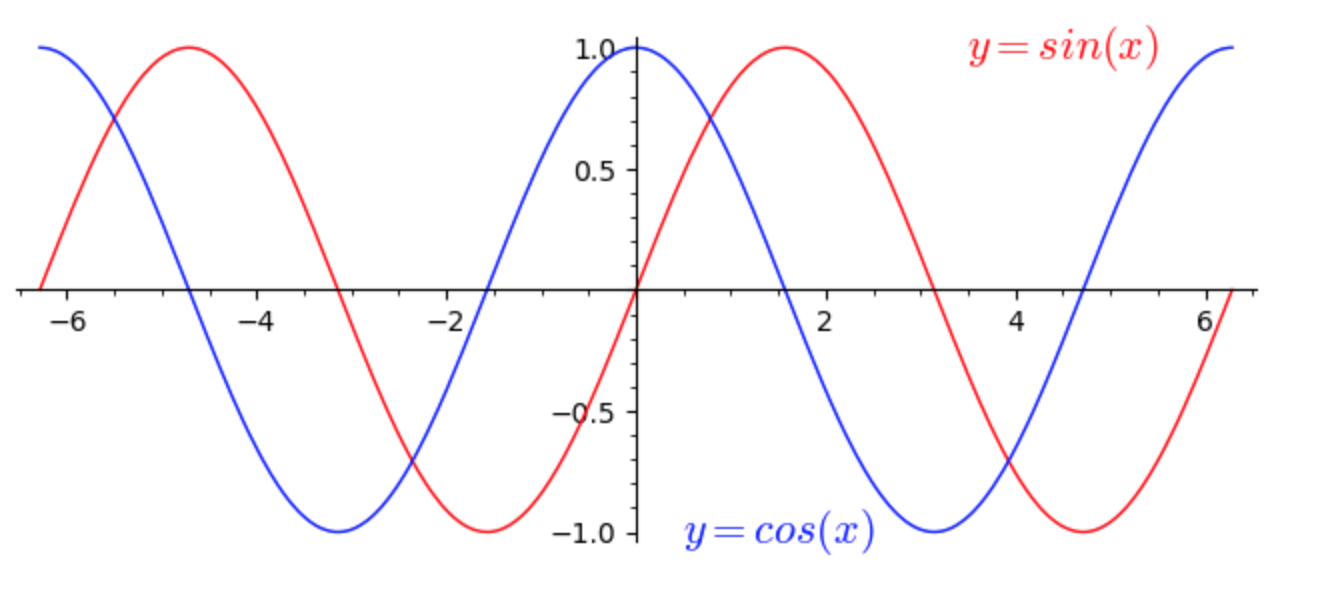
4.1) Le funzioni seno e coseno

Le funzioni seno e coseno sono definite su tutto l’asse reale. Quindi il dominio coincide con l’insieme dei numeri reali \(\mathbb{R}\). Il codominio, cioè l’insieme dei valori assunti, coincide con l’intervallo \([-1,1]\).

Esercizio 4.1
Calcolare il periodo della funzione \(y=\sin 5x\). Disegnare il grafico.
Soluzione: \(\left[p=\dfrac{2\pi}{5}\right]\)

Esercizio 4.2
Calcolare il periodo e disegnare il grafico delle seguenti funzioni:

\[ \begin{array}{l} y = \sin 2\left(x+ \dfrac{\pi}{3}\right) \\ y= 3 \cos \left(x + \dfrac{\pi}{3}\right) \end{array} \]

4.2) La funzione tangente

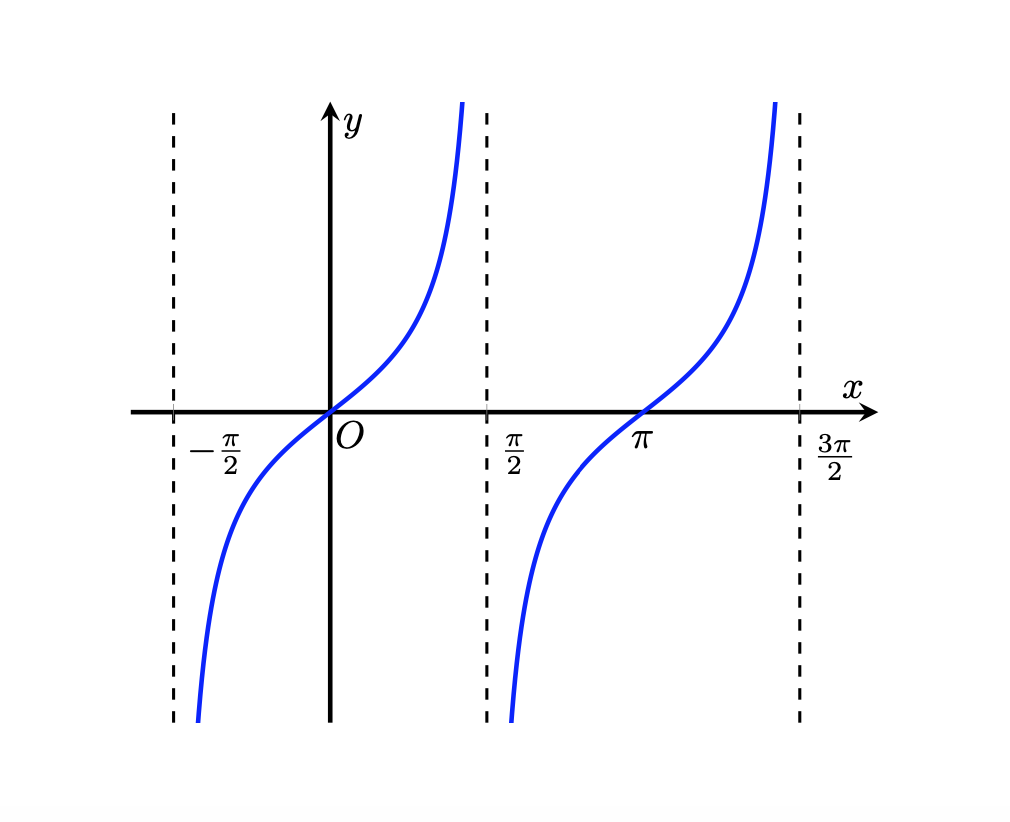
La tangente è una funzione dispari con periodo \(\pi\) ed è illimitata. Non è definita nei punti \(x_{k}=\left (2k+1\right)\dfrac{\pi}{2}, k=0, \pm 1,\pm2, \cdots\). Nelle vicinanze di questi punti la funzione tende ai valori \(\pm \infty\) e si avvicina, senza mai toccarle, alle rette \(x= \left(2k+1\right)\dfrac{\pi}{2}\), chiamate asintoti verticali.

4.3) La funzione cotangente

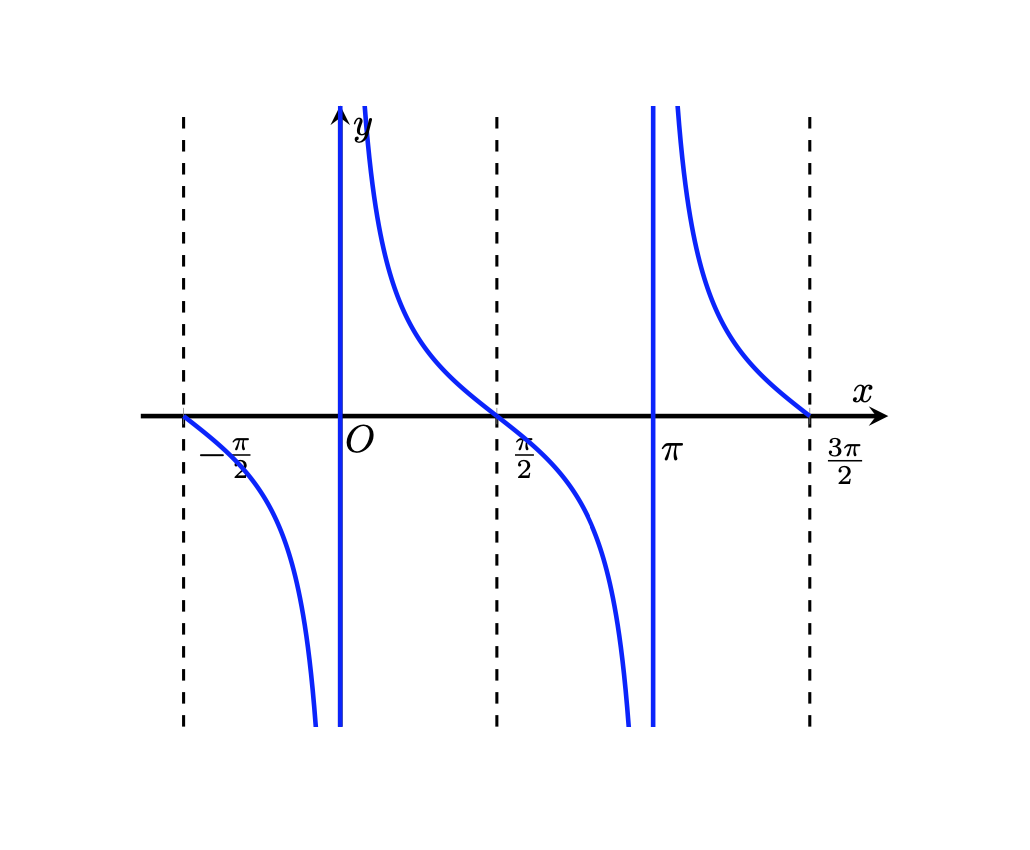
La cotangente è una funzione dispari con periodo \(\pi\) ed è illimitata. Non è definita nei punti \(x_{k}= k\pi, k=0, \pm 1,\pm2, \cdots\). Nelle vicinanze di questi punti la funzione tende ai valori \(\pm \infty\) e si avvicina, senza mai toccarle, alle rette \(x= k\pi\), chiamate asintoti verticali.

Esercizio 4.3
Disegnare il grafico delle seguenti funzioni:

\[ \begin{array}{l} y = \tan \left(x + \dfrac{\pi}{6}\right) \\ y= \cot \left(x + \dfrac{\pi}{4}\right) \end{array} \]

Esercizio 4.4
Dimostrare, senza utilizzare i teoremi dell’analisi matematica, che

\[ \lim_{n \to \infty} n \sin \left(\frac{x}{n}\right)=x \]

Dimostrazione
Per la dimostrazione utilizziamo la formula \(\sin 2x=2 \sin x \cos x\), che vedremo nei paragrafi successivi.
Possiamo supporre \( x \gt 0\). In base alla formula sopra ricordata abbiamo

\[ \sin x= 2 \sin \frac{x}{2}\cos \frac{x}{2} =2 \tan \frac{x}{2}\left(1- \sin^{2}\frac{x}{2}\right) \]

Ricordando che \(\sin x \le x \) e \( \tan x \ge x \) dimostrare la seguente disuguaglianza:

\[ x -\frac{1}{4}\frac{x^{3}}{n^{2}} \le n \sin \frac{x}{n} \le x \]

Quindi concludere la dimostrazione.

Esercizio 4.5
Sfruttando il risultato precedente dimostrare, sempre con metodi elementari, che

\[ \begin{array}{l} \lim\limits_{x \to 0} \dfrac{\sin x}{x}= 1 \\ \lim\limits_{x \to 0} \dfrac{\cos x – 1}{x}= 0 \\ \end{array} \]

5) Le funzioni trigonometriche inverse

In base alla definizione, una funzione \(y=f(x)\) associa ad ogni elemento \(x\) del dominio un unico elemento \(y\) del condominio. Se la funzione è iniettiva allora è possibile invertire il ruolo delle variabili \(x,y\) e considerare la funzione inversa \(x=f^{-1}(y)\), la quale associa ad ogni elemento \(y\) un unico elemento \(x\).
Ad esempio, se \(y=f(x)=5x+ 8\) allora la funzione inversa è \(x=f^{-1}(y)= \dfrac{y-8}{5}\).
Le funzioni seno, coseno e tangente non sono funzioni iniettive, quindi non è possibile determinare le funzioni inverse su tutto il codominio. Tuttavia, se ci si limita ad un parte del codominio è possibile definire le funzioni inverse.

Esempio 5.1 – La funzione inversa del seno

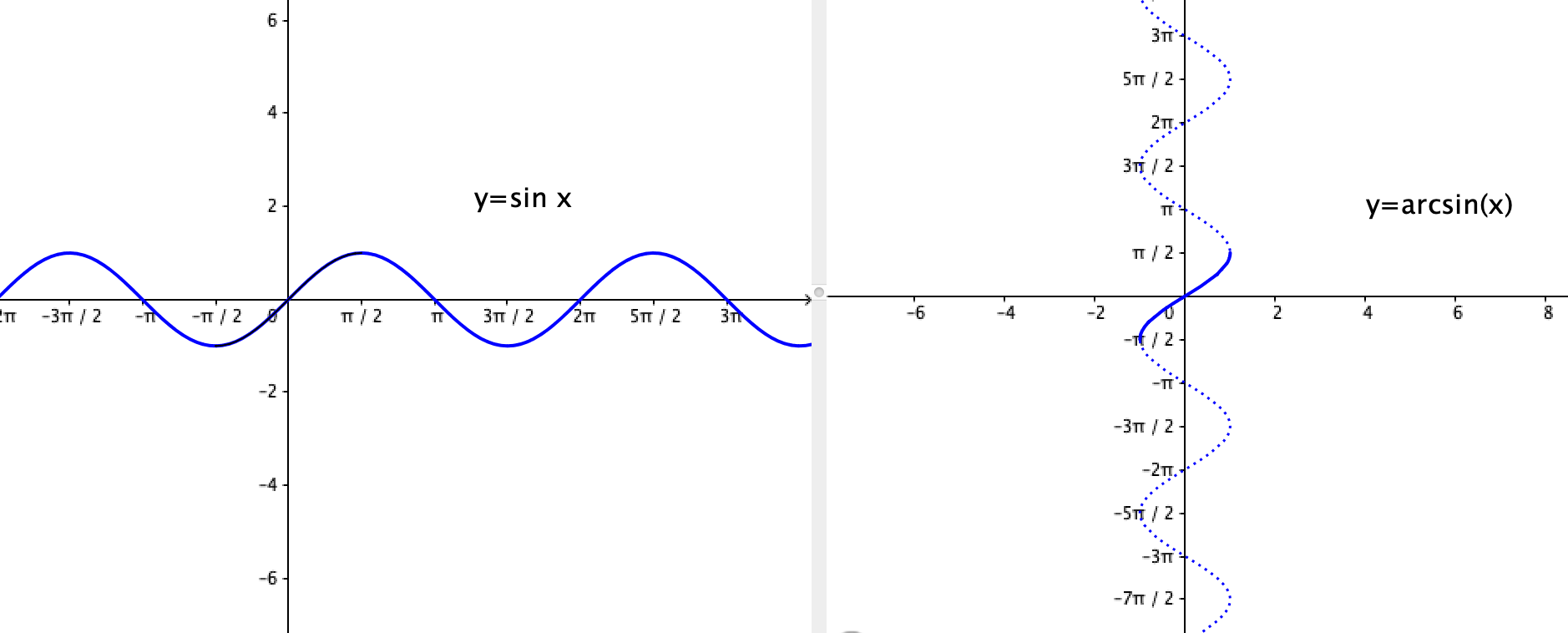
La funzione inversa del seno \(y=\sin^{-1}x\) viene anche indicata con \(y =\arcsin x\). Il dominio e il codominio sono i seguenti:

\[ \begin{array}{l} y= \arcsin x \ ,\quad x \in [-1,+1] \ ,\quad y \in \left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right] \end{array} \]

La tabella seguente riassume le definizioni delle tre funzioni inverse:

\[ \begin{array}{|c|c|c|} \hline \text{funzione} & \text{dominio} & \text{codominio} \\ \hline \arcsin x & [-1,1] & \left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right] \\ \hline \arccos x & [-1,1] & [0,\pi] \\ \hline \arctan x & [-\infty,\infty] & \left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right) \\ \hline \end{array} \]

Esercizio 5.1
Dimostrare le seguenti identità:

\[ \begin{array}{l} \arccos (x) + \arccos (-x)= \pi \\ \arcsin (x) + \arccos(x) = \dfrac{\pi}{2} \\ \arctan(x)=-\arctan(-x) \end{array} \]

Esercizio 5.2

\[ \begin{array}{l} \sin \left(\arcsin \dfrac{1}{2}\right)= \dfrac{1}{2}\\ \arcsin \left( \sin \dfrac{\pi}{3}\right)= \dfrac{\pi}{3} \\ \sin (2 \arctan 3) = \dfrac{3}{5} \end{array} \]

6) Trigonometria del triangolo

Per ogni triangolo ci sono \(6\) elementi che devono essere calcolati: \(3\) lati e \(3\) angoli. I valori di queste \(6\) grandezze non sono indipendenti. Ad esempio se conosciamo due angoli, anche il terzo è determinato, in quanto la somma dei tre deve essere \(180\) gradi. Tuttavia sappiamo che la conoscenza dei tre angoli non è sufficiente per determinare le lunghezze dei lati, in quanto tutti i triangoli simili fra loro hanno gli stessi angoli. Il problema della risoluzione di un triangolo consiste nel determinare quante di queste grandezze è necessario conoscere, per poter calcolare anche le restanti.

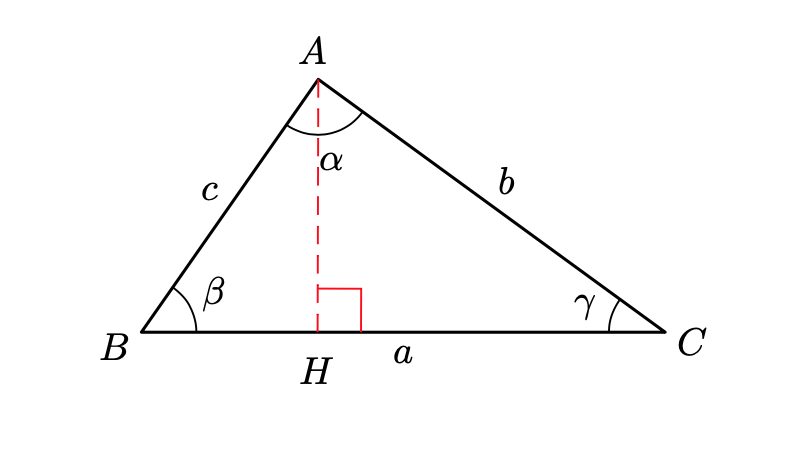
Possiamo dividere il problema della risoluzione del triangolo nei seguenti casi:

\[ \begin{array}{|c|c|c|} \hline \text{Caso} & \text{Dati conosciuti} & \text{Dati da calcolare} \\ \hline LLL & \text{I tre lati } & \text{I tre angoli} \\ \hline LAL & \text{Due lati e l’angolo compreso fra essi } & \text{Un lato e due angoli} \\ \hline LLA & \text{Due lati e l’angolo opposto ad uno dei due lati } & \text{Un lato e due angoli} \\ \hline ALA & \text{Un lato e i due angoli adiacenti } & \text{Due lati ed un angolo} \\ \hline AAL & \text{Un lato e due angoli, non entrambi adiacenti } & \text{Due lati ed un angolo} \\ \hline \end{array} \]

Se il triangolo è rettangolo la soluzione è abbastanza semplice, dato che un angolo ha il valore fissato uguale a \(90^{\circ}\) e inoltre si può utilizzare il teorema di Pitagora. Ad esempio se si conosce l’ipotenusa ed un cateto si può procedere in questo modo:

• Calcolare l’altro cateto tramite il teorema di Pitagora.
• Calcolare il seno di uno degli angoli acuti tramite il rapporto del cateto opposto e l’ipotenusa.
• Determinare l’angolo mediante la funzione inversa del seno.

Oltre al seno si possono usare anche le altre funzioni trigonometriche, in particolare il coseno e la tangente.
Per i triangoli rettangoli vale il seguente teorema:

Teorema 6.1
Un triangolo rettangolo può essere risolto in ognuno dei seguenti casi:
a) si conosce un lato e un angolo acuto
b) si conoscono le lunghezze di due lati

Esercizio 6.1
Definire un algoritmo di soluzione per ognuno dei \(5\) casi elencati in precedenza.

Il problema diventa più difficile nel caso di triangoli obliqui, non rettangoli, in quanto servono più informazioni. Vale il seguente teorema:

Teorema 6.2
Un triangolo generico può essere risolto se sono conosciuti tre dei suoi elementi, e uno è la lunghezza di un lato.

Presentiano ora due teoremi fondamentali, la legge dei seni e la legge dei coseni, utili per risolvere il problema del triangolo nel caso generale.

6.1) Legge dei seni

Teorema 6.3
Sia dato il triangolo generico della figura 6.1. Allora

\[ \frac{a}{\sin \alpha}= \frac{b}{\sin \beta}= \frac{c}{\sin \gamma} \]

Dimostrazione
In relazione alla figura 6.1 abbiamo \(\overline{AH}=c \sin \beta = b \sin \gamma\). Dividendo per \(\sin \beta \cdot \sin \gamma\) otteniamo

\[ \frac{c}{\sin \gamma}= \frac{b}{\sin \beta} \]

In modo analogo otteniamo le formule per le altre coppie di lati e angoli.

Esercizio 6.2 – Legge dei seni estesa
Supponiamo che un triangolo sia inscritto in un cerchio di raggio \(R\). Dimostrare che vale la seguente relazione:

\[ \frac{a}{\sin \alpha}= \frac{b}{\sin \beta}= \frac{c}{\sin \gamma}= 2R \]

Suggerimento
Tracciare il diametro che passa per un vertice del triangolo inscritto. Quindi ricordare che un triangolo inscritto in una semicirconferenza è rettangolo, e che due angoli alla circonferenza che insistono sullo stesso arco sono uguali.

6.2) Legge dei coseni (teorema di Carnot)

Il teorema di Carnot è una generalizzazione del teorema di Pitagora. Facciamo riferimento alla figura 6.1.

Teorema 6.4 – Carnot
Dato un triangolo \(ABC\), con l’angolo \(\gamma\) opposto al lato \(AB\), si ha:

\[ c^{2}=a^{2}+ b^{2}- 2ab \cos \gamma \]

Dimostrazione
Per la dimostrazione applicare il teorema di Pitagora ai due triangoli \(AHB\) e \(AHC\), quindi semplificare.

Mediante il teorema dei seni e il teorema dei coseni è possibile risolvere il problema del triangolo, nel caso generale. Ad esempio, se si conoscono i tre lati possiamo calcolare il valore di due angoli applicando due volte il teorema di Carnot, quindi calcolando il terzo angolo come differenza fra l’angolo di \(180\) gradi e la somma dei due calcolati.

Esercizio 6.3
Definire un algoritmo di soluzione per ognuno dei \(5\) casi elencati in precedenza, nel caso del triangolo generico.

6.3) Area di un triangolo

La formula classica per calcolare l’area \(S\) di un triangolo è

\[ S=\dfrac{\text{base x altezza}}{2} \]

Se non si conosce l’altezza, ma si conoscono due lati e l’angolo fra essi compreso, allora si può usare la formula del teorema seguente. Facciamo riferimento alla figura 6.1.

Teorema 6.5
L’area \(S\) di un triangolo è data dalle seguenti espressioni:

\[ \begin{array}{l} S = \dfrac{1}{2}a b \sin \gamma \\ S = \dfrac{1}{2}a c \sin \beta \\ S = \dfrac{1}{2}b c \sin \alpha \\ \end{array} \]

Dimostrazione
L’area del triangolo è \(S=\dfrac{1}{2}\overline{BC}\cdot \overline{AH}\). Dalla definizione del seno abbiamo

\[ \overline{AH}=\overline{AC} \sin \gamma \]

Dalle precedenti relazioni abbiamo

\[ S=\dfrac{1}{2}\overline{BC}\cdot \overline{AH}=\dfrac{1}{2}\overline{BC} \cdot \overline{AC} \sin \gamma \]

Allo stesso modo si dimostrano le altre due formule:

\[ \begin{array}{l} S=\dfrac{1}{2}\overline{AB} \cdot \overline{BC} \sin \beta \\ S=\dfrac{1}{2}\overline{AB} \cdot \overline{AC} \sin \alpha \\ \end{array} \]

6.4) Formula di Erone

Prima di esporre la formula di Erone risolviamo i seguenti esercizi. Indichiamo con \(p\) il semiperimetro del triangolo (fig. 6.1), cioè

\[ p = \frac{a+b+c}{2} \]

Esercizio 6.4
Dimostrare le seguenti formule

\[ \begin{array}{l} \sin \dfrac{\gamma}{2} = \sqrt{\dfrac{(p-a)(p-b)}{ab} } \\ \cos \dfrac{\gamma}{2} = \sqrt{\dfrac{p(p-c)}{ab}} \\ \end{array} \]

Suggerimento
Utilizzare la legge del coseno e ricordare che

\[ \cos \gamma = 2 \cos^{2}\frac{\gamma}{2}- 1 = 1- 2 \sin^{2}\frac{\gamma}{2} \]

Teorema 6.6 – Formula di Erone

\[ S = \sqrt{p(p-a)(p-b)(p-c)} \ ,\quad \quad p = \frac{a+b+c}{2} \]

Dimostrazione

\[ \begin{array}{l} S = \dfrac{ab\sin \gamma}{2}=\dfrac{ab}{2}\cdot 2 \sin \dfrac{\gamma}{2}\cos \dfrac{\gamma}{2} = \\ ab \cdot \sqrt{\dfrac{(p-a)(p-b)}{ab} }\cdot \sqrt{\dfrac{p(p-c)}{ab}} = \\ \sqrt{p(p-a)(p-b)(p-c)} \end{array} \]

Esercizio 6.5
Siano \(a,b,c\) i lati di un triangolo e \(\alpha,\beta,\gamma\) gli angoli (figura 6.1). Dimostrare la seguente formula di Karl Mollweide (1774–1825) :

\[ \frac{a-b}{c}= \frac{\sin \dfrac{\alpha – \beta}{2}}{\cos \dfrac{\gamma}{2}} \]

7) Le identità trigonometriche

Un’identità trigonometrica è un’espressione contenente funzioni trigonometriche, che risulta valida per tutti i valori degli angoli per i quali sono definite le funzioni trigonometriche presenti. Un esempio è l’identità \(\sin^{2} x + \cos^{2}x=1\).
In generale per dimostrare un’identità trigonometrica si trasforma un membro dell’identità nell’altro, mediante varie sostituzioni.

Esercizio 7.1
Dimostrare le seguenti identità trigonometriche:

\[ \begin{array}{l} \sin 2x = 2 \sin x \cos x \\ \cos 2x = 2\cos^{2}x -1 \\ \tan 2x = \dfrac{2 \tan x}{1- \tan^{2}x} \ ,\quad (x \neq \dfrac{\pi}{2}+ k\pi; x \neq \dfrac{\pi}{4}+ k \dfrac{\pi}{2}) \end{array} \]

Dimostrazione
Dimostriamo soltanto la prima formula. Consideriamo la figura seguente:

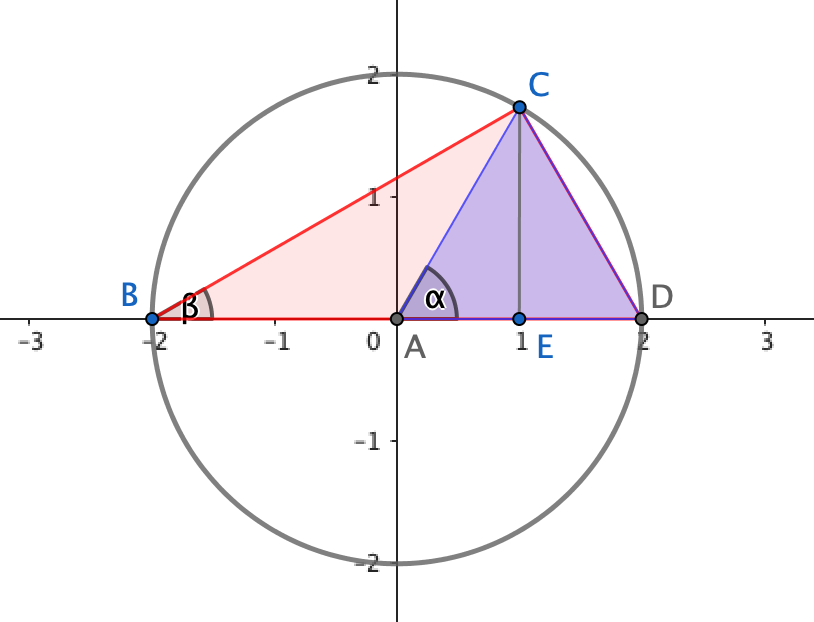
Utilizzando i teoremi di Pitagora ed Euclide abbiamo:

\[ \begin{array}{l} AE = x \ ,\quad EC = y \\ x^{2}+ y^{2}=R^{2} \\ \alpha = 2 \beta \\ \sin \alpha = \dfrac{y}{R} \\ \cos \alpha = \dfrac{x}{R} \\ \sin \beta = \dfrac{y}{\sqrt{2R^{2}+2Rx}} \\ \cos \beta = \dfrac{x+R}{\sqrt{2R^{2}+2Rx}} \\ \sin \beta \cos \beta = \dfrac{y}{2R}= \dfrac{ \sin \alpha}{2} \\ \end{array} \]

7.1) Formule per somma, differenza e prodotto

Teorema 7.1

\[ \begin{array}{l} \sin (x+y) = \sin x \cos y + \sin y \cos x \\ \cos (x+y) = \cos x \cos y – \sin x \sin y \\ \tan (x+y) = \dfrac{\tan x + \tan y}{1- \tan x \tan y} \\ \sin (x-y) = \sin x \cos y – \sin y \cos x \\ \cos (x-y) = \cos x \cos y + \sin x \sin y \\ \tan (x-y) = \dfrac{\tan x – \tan y}{1+ \tan x\ \tan y} \end{array} \]

Dimostriamo soltanto la prima formula, nel caso i due angoli e la loro somma siano angoli acuti.
Consideriamo il seguente triangolo:

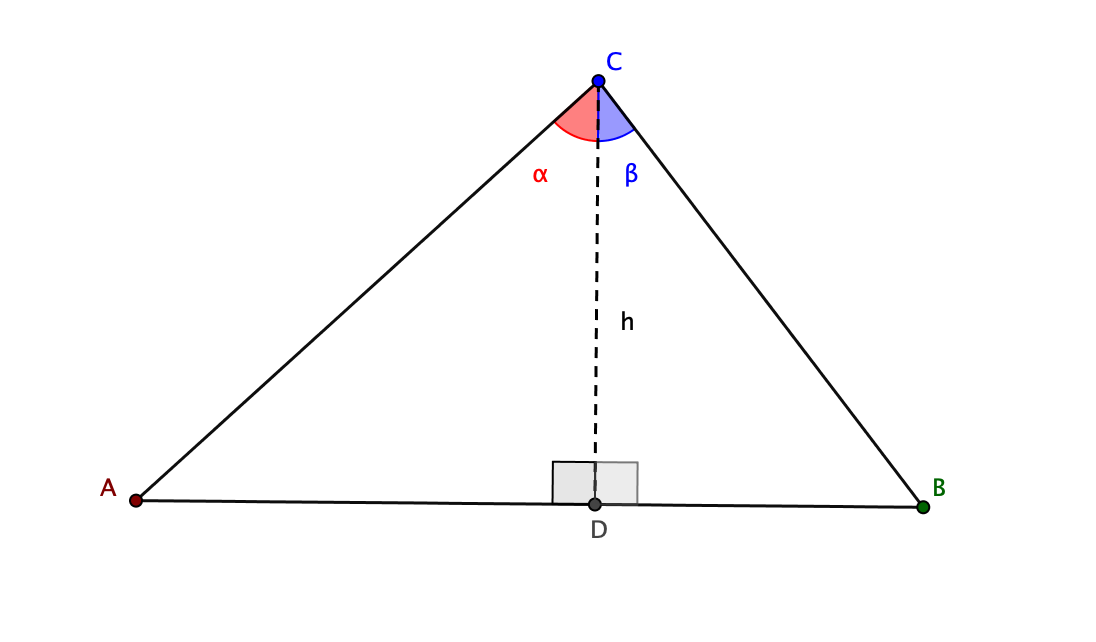
Gli angoli \(\alpha,\beta,\alpha+\beta\) sono acuti. Calcoliamo il \(\sin(\alpha + \beta)\). L’area del triangolo \(\Delta ABC\) è uguale a

\[ S_{1} = \frac{1}{2}\overline{AC}\cdot \overline{BC} \sin (\alpha + \beta) \]

Inoltre dalle definizioni abbiamo

\[ \begin{array}{l} \overline{AD}= \overline{AC}\sin \alpha \ ,\quad h= \overline{AC}\cos \alpha \\ \overline{BD}= \overline{BC}\sin \beta \ ,\quad h= \overline{BC}\cos \beta \\ \end{array} \]

Calcoliamo ora l’area del triangolo totale mediante le formule della geometria elementare:

\[ S_{2} = \frac{1}{2}(\overline{AD}+ \overline{BD})\cdot h = \frac{1}{2}\overline{AD}\cdot h + +\frac{1}{2}\overline{BD} \cdot h = \\ \frac{1}{2}\overline{AC}\cdot \overline{BC}\sin \alpha \cos \beta + \frac{1}{2}\overline{AC}\cdot \overline{BC}\sin \beta \cos \alpha \]

Uguagliando le due espressioni \(S_{1},S_{2}\) abbiamo la formula desiderata. La formula trovata per la somma del seno vale in generale, per qualunque coppia di numeri reali.

Esercizio 7.2
Utilizzando le formule di addizione dimostrare le seguenti formule di prostaferesi:

\[ \begin{array}{l} \sin x + \sin y= 2 \sin \dfrac{x+y}{2}\cos \dfrac{x – y}{2} \\ \sin x – \sin y= 2 \sin \dfrac{x-y}{2}\cos \dfrac{x + y}{2} \\ \cos x + \cos y= 2 \cos \dfrac{x+y}{2}\cos \dfrac{x – y}{2} \\ \cos x – \cos y=- 2 \sin \dfrac{x+y}{2}\sin \dfrac{x – y}{2} \\ \end{array} \]

7.2) Formule di bisezione

A partire dalle formule trovate in precedenza è facile dimostrare le seguenti formule di bisezione.

Teorema 7.2

\[ \begin{array}{l} \sin \dfrac{x}{2}= \pm \sqrt{\dfrac{1-\cos x}{2}} \\ \cos \dfrac{x}{2}= \pm \sqrt{\dfrac{1+\cos x}{2}} \\ \tan \dfrac{x}{2}= \pm \sqrt{\dfrac{1-\cos x}{1+\cos x}} \\ \end{array} \]

Esercizio 7.3
Siano \(\alpha,\beta,\gamma\) gli angoli di un triangolo. Dimostrare le seguenti identità:

\[ \begin{array}{l} \tan \dfrac{\alpha}{2}\tan \dfrac{\beta}{2}+ \tan\dfrac{\alpha}{2}\tan\dfrac{\gamma}{2}+ \tan\dfrac{\beta}{2}\tan\dfrac{\gamma}{2}= 1 \\ \sin \alpha + \sin \beta + \sin \gamma = 4 \cos\dfrac{\alpha}{2} \cos\dfrac{\beta}{2} \cos\dfrac{\gamma}{2} \end{array} \]

Esercizio 7.4
Dimostrare la seguente identità

\[ \frac{4 \cos^{2}x}{\cot \dfrac{x}{2}- \tan \dfrac{x}{2}}= \sin 2x \]

Soluzione
Dalla definizione di tangente e cotangente si ha

\[ \dfrac{4 \cos^{2}x}{\cot \dfrac{x}{2}- \tan\dfrac{x}{2}}= \cos^{2}x \dfrac{\sin \dfrac{x}{2}\cos \dfrac{x}{2}}{\cos^{2}\dfrac{x}{2}- \sin^{2}\dfrac{x}{2}} \]

Dalle formule di duplicazione del seno e del coseno si ottiene con semplici passaggi

\[ \cos^{2}x \dfrac{\sin \dfrac{x}{2}\cos \dfrac{x}{2}}{\cos^{2}\dfrac{x}{2}- \sin^{2}\dfrac{x}{2}}=\dfrac{1}{2}\cos^{2}x \dfrac{\sin x}{\cos x} =\dfrac{1}{4}\sin 2x \]

Questa identità è valida solo se \(\sin x \neq 0\) e \(\cos x \neq 0\). Quindi per tutti i valori di \(x \neq \dfrac{k \pi}{2}\) con \(k\) intero.

7.3) Principio di continuazione analitica

La dimostrazione di molte formule trigonometriche, ad esempio delle formule per la somma e prodotto, può essere lunga e complessa, se si vogliono considerare tutti i casi possibili per i valori degli argomenti.
Un modo più semplice è quello di utilizzare il principio di continuazione analitica. Si tratta di un teorema fondamentale nello studio delle funzioni di una variabile complessa. In termini semplici, data una funzione inizialmente definita in un insieme di numeri reali o complessi, il principio di continuazione analitica permette, sotto certe condizioni, di estendere la funzione ad un dominio più grande reale o complesso.
Le funzioni trigonometriche, che abbiamo definito sull’insieme dei numeri reali, possono essere estese in modo univoco anche nel campo complesso, mediante la formula di Eulero che vedremo in un paragrafo successivo.
Per quanto riguarda le formule della trigonometria, possiamo enunciare il principio nel seguente modo:
Se una identità contenente le funzioni trigonometriche, con operazioni di somma, differenza, prodotto o divisione, è vera per angoli acuti, allora à vera per ogni valore degli angoli.
Ad esempio l’identità \(\sin^{2}+\cos^{2}x=1\), che abbiamo dimostrato nel caso \(0 \le x \le 2\pi\), è valida per ogni valore reale o complesso.

8) Trigonometria e numeri complessi – La formula di Eulero

Eulero nella sua opera ‘Introductio in analysin infinitorum’ \((1748)\) ha dimostrato una formula importante che lega alcune delle principali costanti della matematica:

\[ e^{i\pi}+1 =0 \]

Questa formula è un caso particolare di una formula più generale sempre scoperta da Eulero:

\[ e^{i\theta}=\cos \theta + i \sin \theta \]

Per comprendere la formula di Eulero ricordiamo gli sviluppi in serie di Taylor delle seguenti funzioni, considerate nel campo reale:

\[ \begin{array}{l} e^{x}=\sum\limits_{n=0}^{\infty}\dfrac{x^{n}}{n!}=1 + x + \dfrac{x^{2}}{2!} + \dfrac{x^{3}}{3!} + \dfrac{x^{4}}{4!} + \cdots \\ \\ \sin x =\sum\limits_{n=0}^{\infty}(-1)^{n}\dfrac{x^{2n+1}}{(2n+1)!}= x -\dfrac{x^{3}}{3!} + \dfrac{x^{5}}{5!} -\cdots \\ \\ \cos x =\sum\limits_{n=0}^{\infty}(-1)^{n}\dfrac{x^{2n}}{(2n)!}=1 – \dfrac{x^{2}}{2!} + \dfrac{x^{4}}{4!} -\cdots \\ \end{array} \]

Possiamo definire serie analoghe sostituendo la variabile complessa \(z=x+iy\) al posto della variabile reale \(x\):

\[ \begin{array}{l} e^{z}=\sum\limits_{n=0}^{\infty}\dfrac{z^{n}}{n!} \\ \\ \sin z =\sum\limits_{n=0}^{\infty}(-1)^{n}\dfrac{z^{2n+1}}{(2n+1)!} \\ \\ \cos z =\sum\limits_{n=0}^{\infty}(-1)^{n}\dfrac{z^{2n}}{(2n)!} \\ \end{array} \]

Si tratta di funzioni di variabile complessa, che ad ogni punto del piano complesso associano un numero complesso.
A questo punto per dimostrare la formula di Eulero mettiamo il valore \(z=ix\) nello sviluppo della funzione \(e^{z}\):

\[ \begin{array}{l} e^{ix}=1 + ix + \dfrac{(ix)^{2}}{2!} + \dfrac{(ix)^{3}}{3!} + \dfrac{(ix)^{4}}{4!} + \cdots = \\ \\
1 + ix -\dfrac{x^{2}}{2!} -i\dfrac{x^{3}}{3!} + \dfrac{x^{4}}{4!} + \cdots = \\ \\
\left(1 – \dfrac{x^{2}}{2!} + \dfrac{x^{4}}{4!} – \cdots \right) + i \left(x – \dfrac{x^{3}}{3!} + \dfrac{x^{5}}{5!} + \cdots \right) = \\ \cos x + i \sin x \end{array} \]

Eulero nella sua opera ha espresso la sua formula limitatamente al caso \(x\) reale. Tuttavia la formula è valida anche nel caso complesso: \(e^{iz}=\cos z + i \sin z\). Dalla formula di Eulero segue subito che

\[ \begin{array}{l} e^{2\pi i}=1 \\ e^{-\pi i }=-1 \end{array} \]

Mediante la formula di Eulero un numero complesso può quindi essere rappresentato in questo modo:

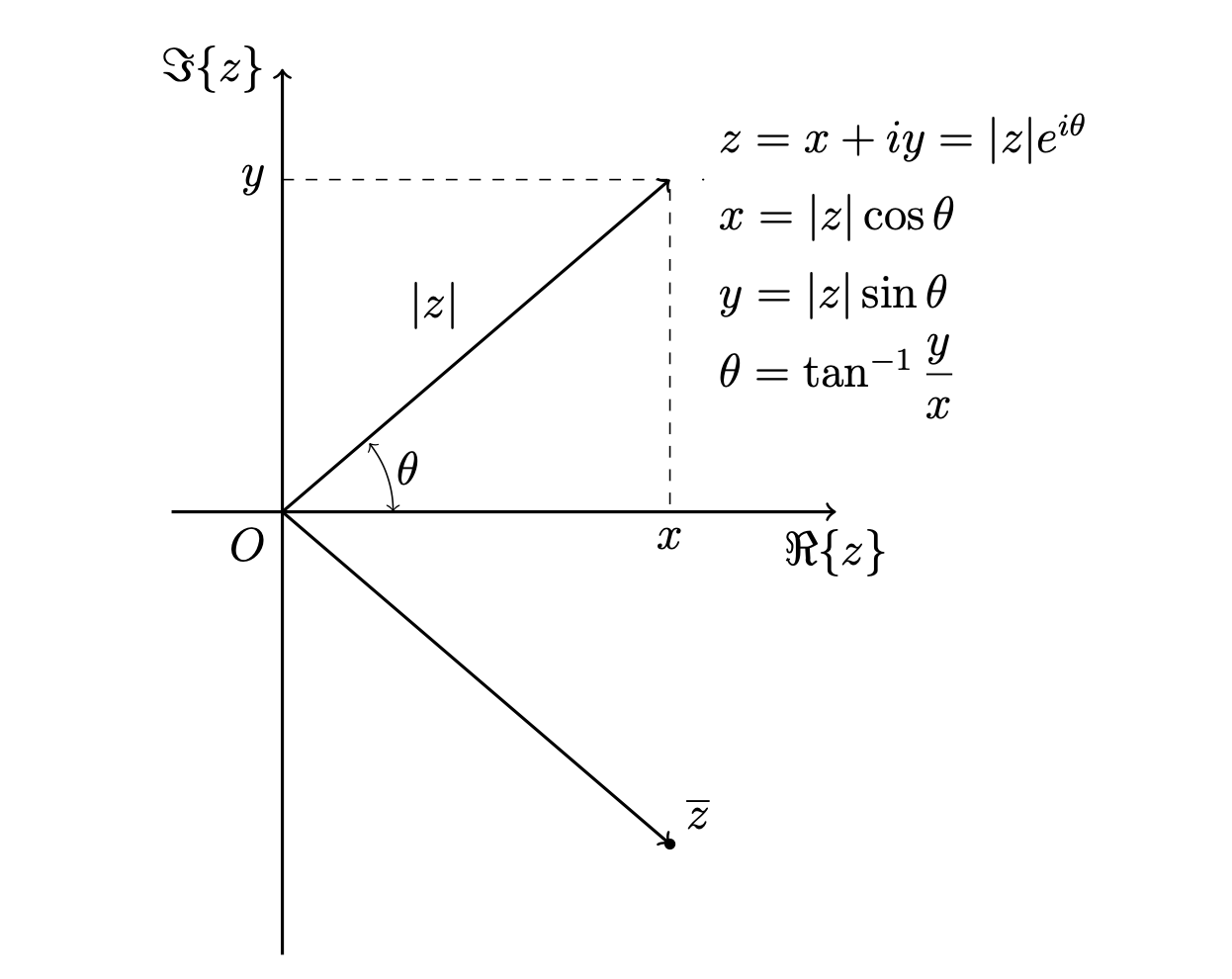
Esempio 8.1
Mediante la formula di Eulero le funzioni trigonometriche possono essere espresse attraverso la funzione esponenziale:

\[ \begin{array}{l} \sin \theta = \dfrac{e^{i\theta}- e^{-i\theta}}{2i} \\ \cos \theta = \dfrac{e^{i\theta}+ e^{-i\theta}}{2} \\ \end{array} \]

Mediante la notazione complessa è possibile dimostrare facilmente diverse identità trigonometriche.

Esercizio 8.1
Dimostrare la seguente identità:

\[ \cos^{3}\theta = \dfrac{1}{4}(\cos 3\theta + 3\cos \theta) \]

Suggerimento
Espandere la formula \(\cos \theta = \dfrac{e^{i\theta}+ e^{-i\theta}}{2}\) e semplificare.

Esercizio 8.2
Dimostrare le seguenti identità:

\[ \begin{array}{l} \sin 3\theta = 3\sin \theta – 4\sin^{3} \theta \\ \tan 3\theta = \dfrac{3\tan \theta – \tan^{3}\theta}{1-3\tan^{2} \theta}\\ \end{array} \]

9) La tangente trigonometrica e la derivata

Consideriamo la seguente figura, in cui è evidenziata la retta tangente alla curva del seno in un punto generico.

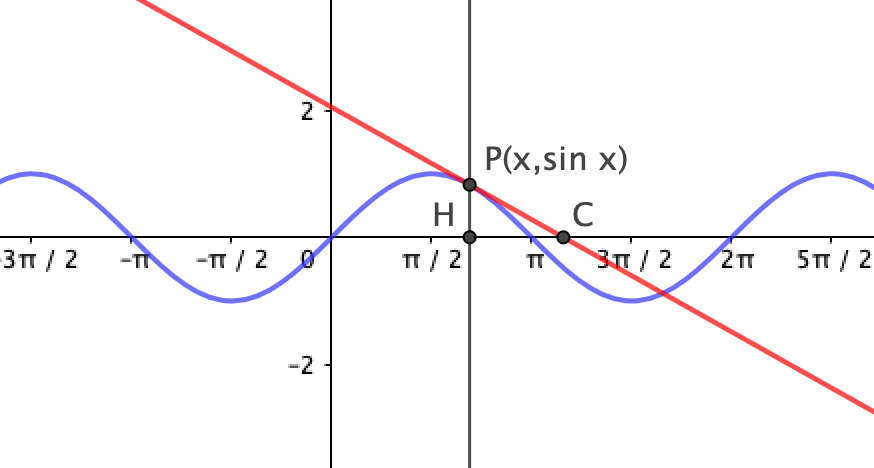
Il problema consiste nel calcolare la pendenza della retta tangente alla curva nel punto \(P=(x,\sin x)\). La pendenza della retta tangente è uguale alla tangente trigonometrica dell’angolo che la retta forma con l’asse delle ascisse. Tale valore si chiama anche coefficiente angolare della retta.
Geometricamente la retta tangente può essere ottenuta partendo dalla retta secante che passa in due punti vicini al punto \(P\): il punto \(A=(x-\Delta x, \sin(x-\Delta x))\) e il punto \(B=(x+\Delta x, \sin(x+\Delta x))\). La pendenza della retta secante è la seguente:

\[ \begin{array}{l} \dfrac{\sin(x+\Delta x) – \sin(x – \Delta x)}{2\Delta x}= \dfrac{2\cos x \sin \Delta x}{2\Delta x}=\cos x \dfrac{\sin \Delta x}{\Delta x} \end{array} \]

dove abbiamo applicato la formula di prostaferesi.
Prendendo la grandezza \(\Delta x\) sempre più piccola, la retta secante che passa per i due punti \(A,B\) si avvicina alla retta tangente nel punto \(P\). Il limite dell’espressione precedente, quando \(\Delta x \to 0\), è per definizione la derivata della funzione \(\sin x\). Poichè \(\lim_{x \to 0}\dfrac{\sin x}{x}=1\) abbiamo quindi

\[ \begin{array}{l} \dfrac{d \sin x}{dx}= \lim\limits_{\Delta x \to 0} \dfrac{\sin(x+\Delta x) – \sin(x – \Delta x)}{2\Delta x}= \cos x \end{array} \]

Quindi il coefficiente angolare della retta tangente nel punto \(P=(x,\sin x)\) è uguale a \(\cos x\). Questo è un risultato valido in generale per ogni curva regolare: la derivata in un punto è uguale al coefficiente angolare della retta tangente in quel punto.

Esercizio 9.1
Dimostrare che la lunghezza del segmento \(\overline{HC}\) nella figura 9.1 è uguale a \(|\tan x|\).

10) Funzioni trigonometriche e serie di Fourier

Il matematico francese Fourier (1768-1830), nella sua opera ‘Teoria analitica del calore’ (1822), introdusse l’idea di sviluppare una funzione periodica mediante una somma infinita contenente le funzioni trigonometriche seno e coseno. Formalmente lo sviluppo in serie di Fourier di una funzione \(f(x)\) periodica, con periodo uguale a \(2L\), è il seguente:

\[ f(x) = \frac{a_{0}}{2}+ \sum\limits_{n=1}^{\infty}\left[a_{n}\cos\frac{n \pi x}{L}+ b_{n}\sin\frac{n \pi x}{L}\right] \]

I numeri reali \(a_{0},a_{1},b_{1},\cdots\) si chiamano coefficienti di Fourier. Supponendo valida l’integrazione per serie, Fourier ottenne le seguenti espressioni per i coefficienti:

\[ \begin{array}{l} a_{n}=\dfrac{1}{L}\int\limits_{-L}^{L}f(x)\cos\dfrac{n \pi x}{L}dx \ ,\quad n=0,1,2,\cdots \\ b_{n}=\dfrac{1}{L}\int\limits_{-L}^{L}f(x)\sin\dfrac{n \pi x}{L}dx \ ,\quad n=1,2,\cdots \\ \end{array} \]

Inizialmente l’idea di Fourier suscitò varie perplessità nei matematici dell’epoca. L’idea che una funzione qualsiasi, anche discontinua in alcuni punti, potesse essere espressa come somma delle funzioni seno e coseno, che sono funzioni continue, venne criticata. Ci sono due aspetti importanti da analizzare:

• in quali casi la serie converge
• anche se la serie converge in un punto \(x\), si deve dimostrare che la somma della serie è uguale al valore \(f(x)\) della funzione nel punto

La dimostrazione delle condizioni nelle quali la serie di Fourier converge al valore della funzione ha richiesto gli sforzi di molti matematici. Il processo è stato lungo e complesso. In particolare, dato che i coefficienti della serie sono degli integrali, è stato necessario definire in modo rigoroso il concetto di integrale, prima con l’integrale di Riemann e successivamente con l’integrale di Lebesgue.
Un teorema importante che individua delle condizioni sufficienti per la convergenza della serie di Fourier è stato dimostrato dal matematico tedesco Dirichlet (1805-1859).

Teorema 10.1 – Dirichlet
Sia data una funzione reale di variabile reale \(f(x)\). Supponiamo che

• la funzione è definita, ad eccezione al massimo di un numero finito di valori, nell’intervallo \([-L,L]\)
• la funzione è periodica con periodo \(2L\), cioè \(f(x+2L)=f(x)\)
• la funzione \(f(x)\) e la sua derivata \(f'(x)\) sono continue a tratti in \([-L,L]\)

Allora la serie di Fourier converge ai seguenti valori:

\[ \begin{array}{l} a) \quad f(x) \quad \text{ se x è un punto di continuità}\\ b)\quad \dfrac{f(x+0)-f(x-0)}{2} \quad \text{ se x è un punto di discontinuità} \end{array} \]

dove \(f(x+0)= \lim\limits_{h \to 0}f(x+h)\) e \(f(x-0)= \lim\limits_{h \to 0}f(x-h)\), con \(h \gt 0\).
Quindi la serie di Fourier converge alla funzione \(f(x)\) in un punto di continuità, mentre converge alla media dei valori destro e sinistro in un punto di discontinuità.

Esempio 10.1
Consideriamo la funzione a gradino (onda quadra) di periodo \(2\pi\) così definita:

\[ f(x) = \begin{cases} = -1 \quad x \in (-\pi,0) \\ = +1 \quad x \in (0,\pi) \end{cases} \]

La funzione è discontinua nel punto \(x=0\) e si può applicare il teorema di Dirichlet. Effettuando i calcoli si trova la seguente serie di Fourier:

\[ f(x)= \frac{4}{\pi}\left(\sin x + \frac{\sin 3x}{3}+ \frac{\sin 5x}{5}+ \frac{\sin 7x}{7}+ \cdots \right) \]

Il diagramma seguente illustra come i primi \(4\) termini della serie di Fourier tendono ad approssimare il grafico della funzione.

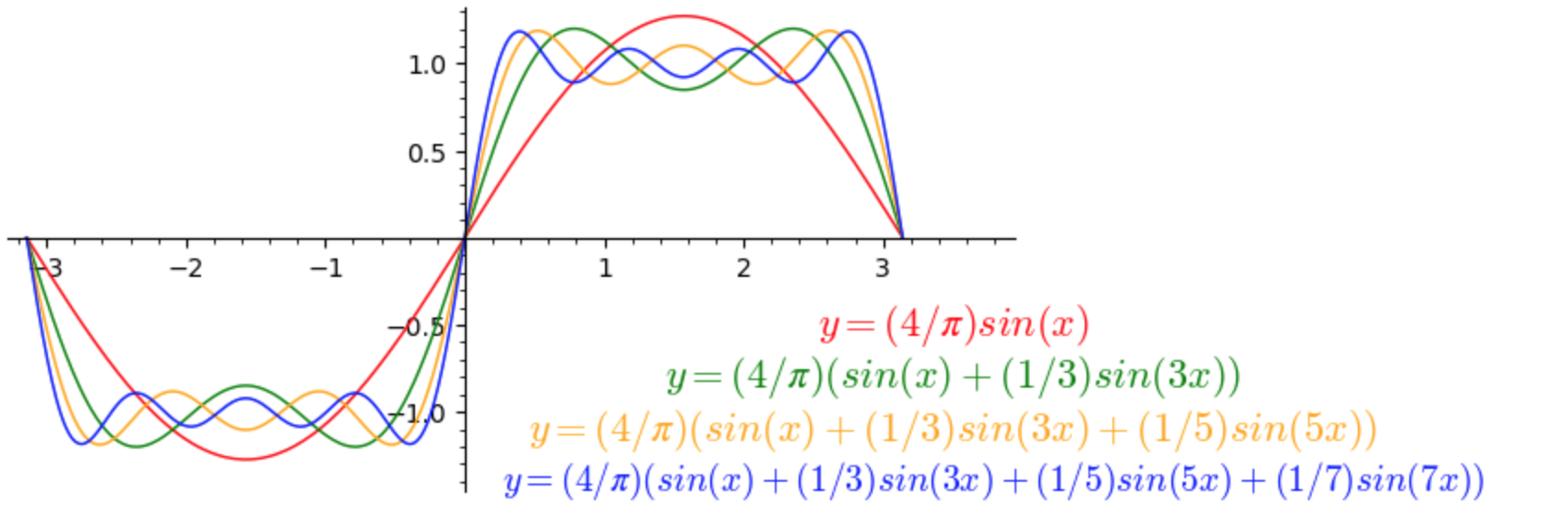
Nelle somme sono presenti solo i termini con il seno, in quanto la funzione a tratti \(f(x)\) è dispari. Nel caso di funzioni pari sono presenti solo i termini con il coseno.
Per una introduzione all’analisi di Fourier vedere ^[3].

11) Esercizi proposti

Proponiamo alcuni esercizi per coloro che vogliono migliorare la comprensione della trigonometria e la capacità di risolvere problemi.

Esercizio 11.1

\[ \sin^{4}\theta = \dfrac{1}{8}(\cos 4\theta – 4\cos 2\theta +3) \]

Esercizio 11.2
Determinare il massimo e il minimo valore della funzione

\[ F(x) = a \cos x + b \sin x + c \]

Soluzione: \(\left[ M=\sqrt{a^{2}+ b^{2}}+c; m = -\sqrt{a^{2}+ b^{2}}+c \right] \)

Esercizio 11.3
Risolvere la seguente equazione trigonometrica:

\[ \sin^{2}x =\cos^{2}x \]

Soluzione: \(\left[x= \dfrac{\pi}{4} +k\pi;x=\dfrac{3\pi}{4} +k\pi; k \in \mathbb{Z}\right]\)

Esercizio 11.4
Sia \(\alpha + \beta + \gamma = \pi\). Allora

\[ \begin{array}{l} \cos 2\alpha + \cos 2\beta + \cos 2\gamma = 1- 4 \cos \alpha \cos \beta \cos \gamma \end{array} \]

Esercizio 11.5
Risolvere la seguente equazione trigonometrica:

\[ \cos \theta = \frac{1}{2} \]

Soluzione: \(\left[\dfrac{\pi}{3}+ 2\pi k; \dfrac{5\pi}{3}+ 2\pi k; k \in \mathbb{Z}\right]\)

Esercizio 11.6
Risolvere la seguente equazione trigonometrica quadratica:

\[ \sin^{2}x – \sin x – 2= 0 \ ,\quad 0 \le x \lt 2\pi \]

Soluzione: \(\left[x= \dfrac{3\pi}{2}\right]\)

Esercizio 11.7
Dimostrare la seguente identità:

\[ \cos \frac{\pi}{65} \cos \frac{2\pi}{65} \cos \frac{4\pi}{65} \cos \frac{8\pi}{65} \cos \frac{16\pi}{65} \cos \frac{32\pi}{65}= \frac{1}{64} \]

Suggerimento
Moltiplicare e dividere per \(2 \sin \dfrac{\pi}{65}\). Quindi accorpare utilizzando la formula di duplicazione del seno \(\sin 2x = 2\sin x \cos x\).

Esercizio 11.8
Risolvere la seguente disequazione:

\[ \sin x \gt \frac{1}{2} \]

Soluzione: \(\left[\dfrac{\pi}{6}+ 2 \pi k \lt x \lt \dfrac{5\pi}{6}+ 2\pi k; k \in \mathbb{Z}\right]\)

Esercizio 11.9
Dimostrare le seguenti formule, utilizzando gli sviluppi di Taylor delle funzioni trigonometriche riportate in precedenza:

\[ \begin{array}{l} \lim\limits_{x \to 0}\dfrac{\sin x}{x}=1 \\ \lim\limits_{x \to 0}\dfrac{\cos x – 1}{x}=0 \\ \end{array} \]

Esercizio 11.10
Mediante l’esercizio precedente e le formule per la somma di due angoli calcolare le seguenti derivate:

\[ \begin{array}{l} \dfrac{d \sin x}{dx}=\lim\limits_{h \to 0}\dfrac{\sin(x+h) – \sin x}{h}= \cos x \\ \dfrac{d \cos x}{dx}=\lim\limits_{h \to 0}\dfrac{\cos(x+h) – \cos x}{h}= -\sin x \\ \end{array} \]

Esercizio 11.11

\[ \sin x + \sin 2x + \cdots + \sin nx = \frac{\sin \frac{(n+1)x}{2}}{\sin \frac{x}{2}} \sin \frac{nx}{2} \]

Suggerimento
Utilizzare il metodo di induzione.

Esercizio 11.12
Calcolare la media aritmetica dei seguenti \(n\) angoli:

\[ \{\alpha, \alpha + \delta, \alpha +2 \delta, \cdots, \alpha + (n-1)\delta\} \]

Soluzione: \(\left[\alpha + \dfrac{(n-1)\delta}{2}\right]\)

Esercizio 11.13
Calcolare il valore della seguente somma:

\[ S=\sin \alpha + \sin(\alpha+\delta) + \sin(\alpha+2\delta) + \cdots + \sin(\alpha+(n-1)\delta) \]

Soluzione: \(\left[S= \sin \left(\alpha+\dfrac{n-1}{2}\delta\right)\cdot \dfrac{\sin \dfrac{n\delta}{2}}{\sin \dfrac{\delta}{2}}\right]\)

Esercizio 11.14
Utilizzando l’esercizio precedente dimostrare che il valore medio della funzione seno nell’intervallo \((0,x)\) è uguale a

\[ \overline{\sin x}= \frac{1-\cos x}{x} \]

Suggerimento
Dividere l’intervallo \([0,x]\) in \(n\) parti \(x=n\delta\). Quindi ricordare che \(\lim_{x \to 0}\dfrac{\sin x}{x}=1\).
Notiamo che è possibile ottenere immediatamente lo stesso risultato mediante il calcolo integrale:

\[ \overline{\sin x} = \frac{1}{x} \int\limits_{0}^{x} \sin x \;dx =\frac{1-\cos x}{x} \]

Esercizio 11.15
Ricordiamo che un numero razionale \(x\) è un numero reale che può essere espresso come rapporto di due numeri interi: \( x = \dfrac{a}{b}, b \neq 0\).
Determinare quali dei seguenti numeri sono razionali:

\[ \begin{array}{l} \cos 60^{\circ} \\ \sin 60^{\circ} \\ \cos 36^{\circ} \\ \end{array} \]

Esercizio 11.16
Dimostrare la seguente identità

\[ \frac{\sin x – \cos x + 1}{\sin x + \cos x – 1}=\frac{\sin x + 1 }{\cos x} \]

Esercizio 11.17 – Viete (1540 – 1603)
Dimostrare la seguente formula delle tangenti (rif. figura 6.1):

\[ \frac{\tan \dfrac{\alpha + \beta}{2}}{\tan \dfrac{\alpha – \beta}{2}}= \dfrac{a+b}{a-b} \]

Per esercitarsi con i problemi di trigonometria vedere ad esempio il testo ^[2].

Conclusione

Lo sviluppo iniziale della trigonometria è stato sollecitato dalle esigenze dell’astronomia, in particolare per l’osservazione e il calcolo delle posizioni e dei movimenti dei pianeti e delle stelle. I progressi iniziali hanno riguardato soprattutto la trigonometria sferica, la quale studia i triangoli disegnati su una superficie sferica, per i quali la somma degli angoli è maggiore di \(180^{\circ}\).
Lo sviluppo di funzioni tramite serie trigonometriche di Fourier ha contribuito ad ampliare grandemente il campo di applicazione della trigonometria. Le funzioni trigonometriche costituiscono ormai uno strumento essenziale in molti settori della matematica, della scienza e della tecnologia.

---

Bibliografia

^[1]Glen Van Brummelen – The Mathematics Of The Heavens And The Earth: The Early History of Trigonometry (New Publisher)

^[2]Alexander Rozenblyum, Leonid Rozenblyum – Learning Trigonometry By Problem Solving (WSPC)

^[3]M. Spiegel – Schaum’s Outline of Fourier Analysis with Applications to Boundary Value Problems (McGraw-Hill)