Le Diverse Concezioni della Probabilità (classica, frequentista e soggettivista) e gli Assiomi di Kolmogorov

La teoria della probabilità, nata soprattutto per esigenze dovute ai giochi d’azzardo, è diventata una disciplina matematica fondamentale in molti settori della scienza e della tecnologia: fisica, biologia, ingegneria, scienze sociali, ecc.

“Il concetto di probabilità è il più importante della scienza moderna, soprattutto perché nessuno ha la più pallida idea del suo significato.”

Bertrand Russell

Il concetto di probabilità non è affatto semplice, come è sottolineato dalla famosa frase di Bertrand Russell. Tra le principali definizioni proposte dai matematici ricordiamo le seguenti:

• probabilità classica – rapporto fra casi favorevoli e casi totali;
• probabilità statistica (frequentista) – basata sugli esperimenti effettuati, come limite della rapporto fra il numero dei casi di successo e il numero totale degli esperimenti;
• probabilità soggettiva – basata sulla propria valutazione personale in base alle informazioni a disposizione.

In questo articolo descriveremo queste principali definizioni e interpretazioni della probabilità, evidenziando le loro motivazioni e anche le loro limitazioni. Quindi illustreremo la definizione assiomatica di Kolmogorov, che tratta la teoria della probabilità come una disciplina matematica, con i suoi assiomi e concetti primitivi, e rinuncia a dare una interpretazione filosofica del concetto di probabilità.

---

1) Evoluzione del calcolo delle probabilità

La teoria della probabilità è stata creata per analizzare i fenomeni casuali, cioè caratterizzati da un grado di incertezza. Nella realtà quotidiana molti fenomeni o eventi sono caratterizzati da una inevitabile incertezza: il tempo atmosferico, la nascita e la morte, i giochi d’azzardo, la misura delle grandezze fisiche, il risultato di un lancio di una moneta o di un dado, l’estrazione del Lotto, e via dicendo.
In realtà la maggior parte dei fenomeni naturali sono caratterizzati da un grado di casualità più o meno elevato, e raramente sono prevedibili con la certezza assoluta. Anche se si conoscono le equazioni matematiche che regolano i fenomeni naturali, in genere si tratta di equazioni non lineari molto complesse, impossibili da risolvere in modo esatto. Con i moderni computer si possono calcolare delle soluzioni approssimate, sicuramente utili, ma che non permettono previsioni certe a lungo termine. In molti casi il massimo che si può fare sono delle previsioni statistiche.
Le applicazioni iniziali del calcolo delle probabilità hanno riguardato i giochi d’azzardo, come il lancio dei dadi, i giochi di carte, ecc. Si tratta di modelli abbastanza semplici, che hanno permesso di analizzare e scoprire le leggi statistiche che regolano questi esperimenti casuali. Tra i primi matematici che hanno studiato questi fenomeni dal punto di vista matematico ricordiamo Gerolamo Cardano (1501-1576), che ha scritto un libretto, il ‘Liber de Ludo Aleae’, in cui ha studiato alcuni problemi tipici, come il lancio dei dadi, e ha abbozzato una semplice definizione di probabilità (vedi Cardano).
La prima definizione precisa dei concetti base della teoria della probabilità è stata fatta da Pascal, Fermat, Huygens (vedi Pascal/Fermat e Huygens).
Nel periodo successivo sono state ampliate le basi teoriche e nel corso del secolo XVIII l’ambito di applicazione è stato esteso in molti altri settori, come gli esperimenti scientifici, le scienze sociali, le assicurazioni.
Il trattato ‘Ars Conjectandi’ di Jacob Bernoulli (1654-1705) costituisce uno dei primi testi scientifici sul calcolo delle probabilità. Nel testo di Bernoulli in particolare vengono studiate le proprietà della distribuzione binomiale, e viene esposta una prima formulazione della legge dei grandi numeri, secondo la quale, ripetendo un esperimento nelle stesse condizioni un numero grande di volte, la frequenza di un evento si avvicina alla sua probabilità.
Nel periodo successivo De Moivre (1667-1754), Laplace (1749-1827), Chebyshev (1821-1894) e altri matematici scoprirono e dimostrarono il teorema del limite centrale, secondo il quale la somma di variabili aleatorie indipendenti e dotate della stessa distribuzione tende ad una distribuzione approssimativamente normale o gaussiana.
Laplace in particolare è stato uno dei protagonisti nello sviluppo della moderna teoria della probabilità, e nell’ampliamento del suo campo di applicabilità, non più limitato ai giochi d’azzardo, ma esteso alle scienze fisiche e sociali. In particolare Laplace comprese la grande utilità del calcolo delle probabilità per analizzare gli inevitabili errori nelle osservazioni e misurazioni, effettuate nei diversi campi della scienza e della tecnologia.

“Les questions les plus importantes de la vie ne sont, pour la plupart, que des problèmes de probabilité”.

Laplace (Essai philosophique sur les probabilités – 1814)

Nonostante i successi ottenuti nei vari campi di applicazione, la teoria della probabilità era di fatto ancora priva di una solida base matematica, a differenza della geometria, l’algebra o il calcolo differenziale, e restavano forti divergenze fra i matematici sul significato da dare al concetto stesso di probabilità.
La prima definizione rigorosa venne data dal matematico russo Andrey Kolmogorov (1903-1987) nel \(1933\), nel suo testo ‘Concetti fondamentali del calcolo delle probabilità’. Kolmogorov sviluppò una teoria assiomatica, in modo simile alla geometria euclidea, a partire da alcuni assiomi fondamentali. A partire dagli assiomi di base, con i metodi della logica matematica vengono dimostrati i vari teoremi, in modo simile ai teoremi della geometria euclidea.
L’esigenza di assiomatizzazione della teoria della probabilità e di altre parti della matematica era stata espressa da Hilbert (1862-1943) a Parigi, durante il Congresso Internazionale dei Matematici, nel quale presentò \(23\) problemi che avrebbero rappresentato una sfida per i matematici del secolo XX. Nel sesto problema Hilbert propose di estendere il metodo assiomatico anche a settori fuori della matematica, come la fisica e anche la teoria della probabilità, che aveva ormai un ruolo importante anche nello studio delle leggi fisiche.

2) Lo spazio degli eventi di un esperimento casuale

In tutte le scienze sperimentali, come la fisica, la chimica, la biologia, è fondamentale effettuare esperimenti e misurazioni, definendo in modo preciso le condizioni nelle quali si svolge il fenomeno. Osservando e misurando i risultati di esperimenti ripetuti, a parità di condizioni, si può arrivare a scoprire le leggi che governano il fenomeno che si sta studiando. Chiamiamo evento ogni risultato singolo di un esperimento. È importante distinguere due tipi di esperimenti:

• esperimenti deterministici
• esperimenti casuali

In un esperimento deterministico, a parità di condizioni, si può prevedere con certezza che il risultato sarà sempre lo stesso. In questo caso parliamo di eventi certi o impossibili.
Negli esperimenti casuali, che sono fondamentali nella teoria della probabilità, il risultato finale non può essere determinato con certezza in anticipo, ma è determinato da fattori intrinsecamente casuali, oppure deterministici ma talmente complessi da rendere impossibile la previsione. In questo caso abbiamo eventi casuali.
Esempi di esperimenti casuali sono il lancio di monete o dadi, l’estrazione di numeri nel gioco del Lotto, il numero di persone che entrano in un centro commerciale in un dato intervallo di tempo, il decadimento radioattivo degli atomi. Naturalmente la proprietà di un evento di essere certo, impossibile e casuale dipende dall’insieme delle condizioni che sono alla base dell’esperimento.

2.1) Regolarità probabilistica

La teoria della probabilità ha lo scopo di misurare il grado di casualità di un fenomeno e formulare delle leggi, chiaramente non deterministiche, ma comunque utili per studiare i fenomeni.
Anche se non possiamo prevedere il risultato di un esperimento casuale, in genere siamo in grado di determinare l’insieme dei risultati possibili. Nello studio di molti fenomeni, effettuando numero elevato di esperimenti nelle medesime condizioni, si osserva che i risultati degli eventi casuali tendono a concentrarsi intorno ad un valore medio. Questo tipo di regolarità, chiamata probabilistica o statistica, permette di fare delle previsioni quantitative dei possibili risultati di un esperimento, con un certo grado di fiducia.
Un evento casuale o aleatorio è un evento la cui frequenza di realizzazione tende ad un valore limite, all’aumentare del numero delle osservazioni. Questo valore limite si chiama probabilità dell’evento casuale. Quindi ad un evento casuale \(A\) possiamo assegnare un numero \(P(A)\) che indica la probabilità del verificarsi dell’evento, sotto delle condizioni prefissate.
Come abbiamo detto in precedenza lo studio matematico degli eventi casuali ha riguardato inizialmente il gioco d’azzardo, in particolare da parte di Pascal, Fermat, Huygens. In seguito questo concetto è stato ampliato a numerosi altri settori della scienza e della tecnologia.

Esempi di esperimenti casuali

• lancio di una moneta (due possibili risultati)
• lancio di un dado (sei possibili risultati)
• estrazione di una carta da un mazzo di carte di poker
• gioco del lotto
• numero di nascite in un dato periodo dell’anno

Esempio 2.1 – Estrazione di palline da una scatola
Consideriamo una scatola contenente \(4\) palline rosse e \(2\) nere. Supponiamo di effettuare delle estrazioni casuali con restituzione, cioè riammettendo la pallina nella scatola dopo ogni estrazione.
L’estrazione di una pallina dalla scatola è un esperimento aleatorio, mentre l’estrazione di una pallina rossa è un evento aleatorio.
Naturalmente non è possibile prevedere il colore della pallina estratta in una singola estrazione. Tuttavia effettuando un numero elevato di estrazioni, ad esempio \(1000\), si osserva che il numero delle palline rosse si approssima al valore \(\dfrac{2}{3}\) e il numero della palline nere al valore \(\dfrac{1}{3}\).

Esempio 2.2 – Lancio di monete
Il lancio di monete è un classico esempio di esperimento casuale. In ogni lancio ci sono due possibili risultati, testa (T) o croce (C).
Lanciando una moneta \(1000\) volte, se la moneta non è truccata, ci si attende che approssimativamente nel \(50\%\) dei lanci esca testa, e nell’altro \(50\%\) esca croce.

Esempio 2.3 – Decadimento radioattivo di atomi
Il decadimento radioattivo è un processo fisico, in cui alcuni atomi emettono delle radiazioni e modificano la loro configurazione.
Il decadimento radioattivo è un processo casuale. Per ogni atomo c’è una certa probabilità di emettere radiazione in un dato intervallo di tempo. Tuttavia non possiamo prevedere con certezza se un dato atomo decadrà o no entro un secondo.

2.2) Spazio campionario

Il modello matematico alla base della teoria della probabilità utilizza i concetti della teoria degli insiemi e poi, nella formulazione più avanzata, della teoria della misura. A partire dal concetto di esperimento casuale e risultato si definisce lo spazio campionario \(\Omega\), cioè l’insieme di tutti i possibili risultati di un esperimento casuale. Gli eventi sono sottoinsiemi dello spazio campionario \(\Omega\). Lo spazio campionario può essere finito oppure infinito, numerabile o continuo.
Un evento può anche essere interpretato come una entità logica, che può assumere due valori: vero e falso. In altri termini un evento è espresso da una proposizione, che può ammettere solo due risposte: affermativa o negativa.
Nel linguaggio dei giochi d’azzardo un evento corrisponde ad una scommessa che è vinta se l’evento è vero, mentre è persa se l’evento è falso.
È fondamentale definire in modo preciso l’insieme degli eventi che appartengono allo spazio campionario. Questo può essere fatto mediante l’elenco degli eventi possibili (nel caso finito), oppure esprimendo le proprietà che devono avere gli eventi che appartengono ad uno spazio campionario. Possiamo distinguere tra eventi elementari ed eventi composti. Ad esempio, lanciando \(2\) dadi ogni coppia è un evento elementare, mentre l’insieme delle coppie la cui somma è uguale a \(11\) è un evento composto, costituito dall’insieme degli eventi elementari \(\{(5,6),(6,5)\}\). Per analogia con il linguaggio geometrico, gli eventi elementari vengono anche chiamati punti campionari.

Esempio 2.4 – Lancio di monete
Supponiamo di lanciare due monete. Il risultato di ogni lancio può essere testa o croce. Quindi con due monete gli eventi possibili sono le coppie di numeri

\[ \Omega = \{(T,T),(T,C),(C,T),(C,C)\} \]

Quindi \(|\Omega|=2^{2}=4\). Nel caso del lancio di \(n\) monete abbiamo \(|\Omega|=2^{n}\).

Esempio 2.5 – Lancio di dadi
Supponiamo di lanciare due dadi. In questo caso gli eventi possibili sono le coppie di numeri

\[ \Omega = \{(1,1),(1,2), \cdots, (6,5),(6,6)\} \]

Quindi \(|\Omega|=36\). Nel caso del lancio di \(n\) dadi abbiamo \(|\Omega|=6^{n}\).

Esempio 2.6 – Contatore Geiger
Supponiamo di avere un contatore Geiger che registra il conteggio dei raggi cosmici. Abbiamo uno spazio campionario infinito numerabile

\[ \Omega = \{0,1,2,3,\cdots\} \]

Esempio 2.7 – Distribuzione di palline nelle scatole
Supponiamo di avere \(4\) palline distinguibili, da distribuire in modo casuale in \(3\) scatole distinguibili. Il numero delle possibili configurazioni è \(3^{4}=81\).
Nel caso di \(r\) palline distinguibili e \(n\) scatole distinguibili avremo \(n^{r}\) configurazioni possibili.

Esempio 2.8 – Carte da poker
Nel gioco del poker il numero delle possibili configurazioni delle \(5\) carte di un giocatore è \(\binom{52}{5}\). Verificare che il numero delle mani con un poker, cioè con quattro carte dello stesso valore, è

\[ \binom{13}{1}\binom{4}{4}\cdot \binom{12}{1}\binom{4}{1} \]

Esempio 2.9 – Gioco del lotto
Verificare che nel gioco del lotto il numero delle cinquine che si possono estrarre dall’urna che contiene i \(90\) numeri è

\[ \binom{90}{5} = \frac{90 \cdot 89 \cdot 88 \cdot 87 \cdot 86}{5!}=43.949.268 \]

Esempio 2.10
Consideriamo il lancio di due dadi con sei facce e registriamo la somma delle due facce.
Lo spazio campionario è costituito dall’insieme \(\Omega=\{2,3,4,5,6,7,8,9,10,11,12\}\).

Esempio 2.11 – Spazio campionario continuo
In molti casi i risultati dell’esperimento non sono ristretti ai numeri interi, e non è possibile fare l’elenco di tutti i possibili risultati di un esperimento. Ad esempio nel caso dell’altezza di un gruppo di persone, misurata in centimetri, potremmo avere una lista potenzialmente infinita di valori con cifre decimali: \(\{176,25;152,67;121,45;\cdots\}\). Stessa situazione se misuriamo il peso. In questo casi si deve descrivere lo spazio campionario non mediante un elenco, ma mediante una proprietà che caratterizza gli elementi dell’insieme. Ad esempio per l’altezza in centimetri possiamo dire \(\Omega= \{0 \le h \le 250, h \in \mathbb{R}\}\), cioè lo spazio campionario è costituito da tutti i numeri reali compresi nell’intervallo.

2.3) Algebra degli eventi

Gli oggetti fondamentali che studia la probabilità sono gli eventi, cioè i possibili risultati di un esperimento o di un processo casuale. In particolare è importante studiare le relazioni fra gli eventi e le operazioni logiche che è possibile eseguire sugli eventi. Con queste operazioni logiche, simili alle operazioni aritmetiche di addizione e moltiplicazione, viene costruita un’algebra di eventi.
Se gli eventi vengono visti come insiemi, allora utilizziamo il linguaggio della teoria degli insiemi per esprimere le operazioni e le relazioni fra gli eventi.
L’evento \(\Omega\), cioè lo spazio campionario, che corrisponde all’insieme universo, viene chiamato anche evento certo, mentre il sottoinsieme vuoto \(\emptyset\) è un evento impossibile. Due eventi di dicono incompatibili se non possono verificarsi entrambi nello stesso esperimento, in altri termini se sono insiemi disgiunti.
Le principali operazioni sugli eventi sono le seguenti:

Unione di due eventi
Dati due eventi \(A,B\), l’unione \( A \cup B\) è l’evento che consiste di tutti i risultati che sono in \(A\) oppure in \(B\), o in entrambi.

Intersezione di due eventi
Dati due eventi \(A,B\), l’intersezione \( A \cap B\) è l’evento che consiste di tutti i risultati che sono presenti in entrambi \(A\) e \(B\).

Complemento di un evento
Dato un evento \(A\), il complemento \(\overline{A}\), indicato anche con \(A^{c}\), è l’evento che contiene tutti i risultati che non sono in \(A\). In altri termini \(\overline{A}=\Omega \setminus A\). È evidente che \(E \cup \overline{E}= \Omega\) e \(E \cap \overline{E}= \emptyset\).

Un evento può essere interpretato anche come una proposizione logica che può assumere solo due valori logici: \((V,F)\), cioè può essere vero se si verifica nell’esperimento, oppure falso se non si verifica. Quindi le operazioni sugli eventi possono esser espresse come operazioni logiche del calcolo proposizionale. Al posto dei simboli insiemistici per le tre operazioni si possono usare i simboli logici:

• \(\lor\) : somma logica
• \(\land\) : prodotto logico
• \(\neg\) : complemento o negazione logica

Ad esempio, il prodotto logico \(A \land B\) di due eventi \(A,B\) è l’evento che è vero se e solo se sono entrambi veri \(A\) e \(B\). Il complemento o negazione logica \(\neg{A}\) di un evento \(A\) è vero se e solo se \(A\) è falso, ed è falso se e solo se \(A\) è vero.
La seguente tavola di verità illustra le operazioni sugli eventi:

\[ \begin{array}{|c|c|c|c|c|c|} \hline A & B &A \lor B & A \land B & \neg{A}\\ \hline F &F & F & F &V \\ V &F & V & F & F \\ F &V & V & F & V \\ V &V & V & V &F \\ \hline \end{array} \]

Se in un dato esperimento ogni volta che si verifica un evento \(A\) allora si verifica anche l’evento \(B\), diciamo che \(A\) implica \(B\) e utilizziamo la notazione \( A \subset B\), oppure la notazione logica \(A \implies B\).

È facile dimostrare il seguente teorema:

Teorema 2.1

\[ \begin{array}{l} A \cup B = B \cup A \quad \text{proprietà commutativa} \\ A \cup (B \cup C) = (A \cup B) \cup C \quad \text{proprietà associativa } \\ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \quad \text{proprietà distributiva } \\ A \cup A = A \quad \text{proprietà di idempotenza} \\ \end{array} \]

Analoghe proprietà valgono per l’operazione di prodotto di eventi.

Esercizio 2.1 – Leggi di De Morgan
Verificare le seguenti identità:

\[ \begin{array}{l} \overline{ A \cup B} = \overline{A} \cap \overline{B} \\ \overline{ A \cap B} = \overline{A} \cup \overline{B} \\ \end{array} \]

2.4) La funzione probabilità

La probabilità è una misura quantitativa, definita su uno spazio campionario, relativa alla possibilità del verificarsi di un dato evento casuale. Dal punto di vista matematico è una funzione \(P(A)\) che ad ogni evento \(A\) assegna un numero reale non negativo, e che deve soddisfare un insieme di vincoli di coerenza. Due vincoli naturali sono i seguenti:

\[ \begin{array}{l} P(\Omega)=1 \quad \text{(evento certo)} \\ P(\emptyset)=0 \quad \text{(evento impossibile)} \end{array} \]

Nel seguito vedremo altri vincoli di coerenza che la funzione probabilità deve soddisfare.
Il calcolo delle probabilità viene applicato in vari settori della matematica (statistica, fisica, biologia, ingegneria, scienze sociali, ecc.). Le valutazioni quantitative che vengono fatte non sono arbitrarie, ma dipendono in modo determinante dalle proprietà oggettive del fenomeno che si sta studiando, e anche dallo stato di conoscenza dell’osservatore.

3) La definizione classica della probabilità

La definizione classica di probabilità si applica al caso di spazi campionari finiti, in cui gli eventi elementari sono ugualmente probabili, o equiprobabili, cioè ogni evento si può presentare con la stessa possibilità di ogni altro.
Nella definizione classica il concetto di equiprobabilità è considerato un concetto primitivo, che non necessità di una definizione formale. In altri termini è una proprietà oggettiva, derivata dalle caratteristiche di simmetria dell’esperimento. In realtà questo approccio ha dei limiti, in quanto il fatto di valutare l’equiprobabilità come una proprietà oggettiva in ultima analisi dipende dal soggetto e dal suo stato di conoscenza del fenomeno. Soggetti con diversi livelli di conoscenza potrebbero avere opinioni diverse.
Secondo la definizione classica, dato un esperimento che prevede la possibilità di avere un numero finito di casi possibili, la probabilità di un evento \(E\) è definita come il rapporto fra il numero dei casi favorevoli e il numero dei casi possibili:

\[ P(E) = \frac{\text {numero casi favorevoli}}{\text {numero casi possibili}} \]

Esempio 3.1 – Probabilità di un tris a poker
Le carte sono \(52\), di quattro colori. Il tris è costituito da tre carte uguali e due spaiate. Dimostrare che il numero di tris possibili è

\[ \binom{13}{1}\binom{4}{3} \frac{ (12 \cdot 4)(11 \cdot 4)}{2}=54912 \]

La probabilità di avere un tris è quindi

\[ p = \frac{54912}{2598960} \approx 2,11 \% \]

Esercizio 3.1
Supponiamo di lanciare due dadi. La seguente tabella riassume i possibili risultati:

\[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{Somma} & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline \text{Casi favorevoli} & 1 & 2 & 3 & 4 & 5 & 6 & 5 & 4 & 3 & 2 & 1 \\ \hline \end{array} \]

Calcolare la probabilità \(p_{1}\) che la somma dei numeri sia \(7\) e la probabilità \(p_{2}\) che la somma sia un numero dispari.

Soluzione: \(\left[p_{1}=\dfrac{1}{6}; p_{2}=\dfrac{1}{2}\right]\)

Esercizio 3.2
Uno studente gioca con le seguenti lettere dell’alfabeto: \(A,A,A,E,I,C,M,M,T,T\). Calcolare la probabilità che distribuendo a caso le lettere in una riga si ottenga la parola “MATEMATICA”.

Soluzione: \(\left[\dfrac{3!2!2!}{10!}\right]\)

Esercizio 3.3
Verificare che la funzione \(P(.)\) definita su un insieme di eventi dell spazio campionario finito \(\Omega\) soddisfa le seguenti proprietà:

1) per ogni evento \(A\) si ha \(P(A) \ge 0\);
2) per l’evento \(\Omega\) si ha \(P(\Omega)=1\);
3) se un evento \(A\) è decomponibile in due eventi \(B,C\) incompatibili tra loro allora:

\[ P(A)= P(B) + P(C) \]

Esercizio 3.4

\[ \begin{array}{l} P(\overline{A})= 1 – P(A) \\ \end{array} \]

Esercizio 3.5
Se un evento \(A\) implica l’evento \(B\) allora \(P(A) \le P(B)\).

Esercizio 3.6
Dati due eventi \(A,B\) in generale si ha

\[ P( A \cup B) \le P(A) + P(B) \]

Soluzione
Ricordiamo che un insieme non contiene elementi duplicati. Quindi se un punto campionario appartiene ad \(A\) e anche a \(B\), allora viene contato una volta nella parte sinistra e due volte nella parte destra dell’equazione.
Più precisamente vale il seguente teorema:

Teorema 3.1

\[ \begin{array}{l} P( A \cup B) = P(A) + P(B) – P(A \cap B) \\ P( A \cup B \cup C) = \\ P(A) + P(B)+ P(C) – P(A \cap B) – P(A \cap C) – P(B \cap C) + P(A \cap B \cap C) \\ \end{array} \]

Esercizio 3.7
Calcolare la probabilità che ci sia almeno un asso estraendo tre carte da un mazzo di poker di \(52\) carte.

Suggerimento
Risolvere l’esercizio in due modi distinti. Nel primo calcolare le probabilità che ci siano uno, due o tre assi e quindi sommare. Nel secondo calcolare la probabilità che non ci sia nessun asso e quindi calcolare la probabilità dell’evento complementare.
Soluzione: \(\left[ 1- \frac{\binom{48}{3}}{\binom{52}{3}}\right]\)

3.1) Osservazioni sulla definizione classica

La definizione classica ha il vantaggio della semplicità e della facilità di applicazione. Viene applicata in tutti i casi in cui per ragioni di simmetria possiamo considerare tutti gli eventi elementari ugualmente possibili: giochi con le carte, con i dadi, gioco del Lotto, ecc.
La definizione classica ha chiaramente un problema di circolarità autoreferenziale: infatti si usa l’espressione “ugualmente possibili” per evitare una definizione tautologica. In altri termini nella definizione si usa un termine sostanzialmente equivalente a quello che si vuole definire.
Per superare questo problema Laplace, nel suo ‘Saggio filosofico sulle probabilità’ (1814) utilizza il “principio di ragione sufficiente” o “principio di indifferenza“. Secondo questo principio va assegnata la stessa probabilità a due risultati, se non esistono particolari motivi o informazioni che possano far pensare che uno di essi abbia una maggiore o minore possibilità di verificarsi rispetto all’altro.
Un altro limite della definizione classica è dato dal fatto che si applica solo a situazioni in cui lo spazio campionario è finito, mentre in molte situazioni c’è un numero infinito di eventi possibili.

4) La probabilità geometrica

Un limite della definizione classica della probabilità è dovuto al fatto che è limitata a spazi campionari con un numero finito di eventi elementari.
In molti casi è necessario studiare fenomeni che hanno un numero infinito di possibili risultati. La probabilità geometrica permette di estendere la definizione classica a situazioni in cui è necessario studiare le proprietà geometriche, come lunghezze, aree e volumi, di oggetti del spazio. In questo caso lo spazio campionario è un sottoinsieme \(\Omega\) di misura finita dello spazio euclideo \(\mathbb{R}^{n}\), con \(n=1,2,3,\cdots\). Gli eventi sono sottoinsiemi di \(\Omega\). La misura degli eventi può essere la lunghezza (\(n=1\)), la superficie (\(n=2\)) o il volume (\(n=3\)).
La probabilità non viene definita come rapporto fra casi favorevoli e casi totali, ma come rapporto di misura fra insiemi. Gli strumenti matematici utilizzati per il calcolo della probabilità geometrica sono la teoria della misura e il calcolo integrale.
Supponiamo di avere due regioni piane misurabili \(A,B\), con \(A \subset B\), cioè la regione \(A\) è contenuta nella regione \(B\). Allora la probabilità che un punto scelto a caso nell’insieme \(B\) appartenga anche all’insieme \(A\) è data dal rapporto fra le misure delle due regioni:

\[ p = \frac{m(A)}{m(B)} \]

dove il simbolo \(m(A)\) indica l’area della regione piana. Naturalmente la definizione può essere estesa a regioni di qualunque dimensione.

Esempio 4.1
Supponiamo \(\Omega = [-10,10]\). La probabilità che un punto sceso a caso nell’intervallo, sia contenuto nell’intervallo \(A=[1,5]\) è quindi

\[ p = \frac{m(A)}{m(\Omega)}=\frac{4}{20}=\frac{1}{5} \]

Esempio 4.2 – Problema dell’ago di Buffon
Un piano viene suddiviso da rette parallele separate da una distanza \(2L\). Un ago di lunghezza \(2l\), con \(l \lt L\), viene lanciato in modo casuale sul piano. Calcolare la probabilità che l’ago intersechi una delle rette.

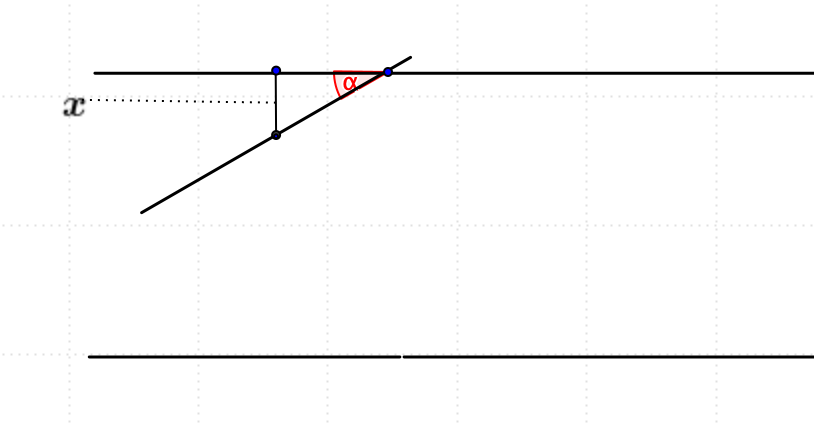
Soluzione
Indichiamo con \(x\) la distanza dal centro dell’ago alla parallela più vicina e con \(\alpha\) l’anglo formato dall’ago con questa parallela.
Dalla figura si vede che affinché l’ago attraversi una delle rette parallele deve verificarsi la seguente relazione:

\[ x \le l \sin \alpha \]

Disegniamo la funzione \(F(\alpha)= l \sin \alpha\), con \(0 \le \alpha \le \pi\), e calcoliamo l’area sottesa dalla curva:

\[ S = \int\limits_{0}^{\pi} l\sin\alpha d\alpha = 2l \]

Quindi la probabilità cercata è data dal rapporto fra l’area sottesa dalla curva e l’area del rettangolo con lati \([0,\pi]\) e \([0,L]\):

\[ p = \frac{2l}{L \pi} \]

Il metodo Montecarlo per il calcolo di \(\pi\)
Laplace nel \(1812\) suggerì di utilizzare l’esperimento di Buffon per calcolare il valore approssimato di \(\pi\).
Supponiamo di lanciare l’ago un certo numero \(n\) di volte. Supponiamo che tocchi una parallela \(m\) volte. Allora possiamo approssimare la probabilità \(p\):

\[ p = \frac{m}{n} \]

Inserendo questo valore nella formula ricavata in precedenza e risolvendo rispetto a \(\pi\), abbiamo:

\[ \pi \approx \frac{2ln}{Lm} \]

Nel \(1901\) il matematico Lazzarini effettuò una simulazione di questo tipo. Scelse un ago lungo \(\dfrac{5}{6}\) della distanza fra due rette parallele. Lasciò cadere \(3408\) volte un bastoncino su un foglio con righe paralelle. Il bastoncino intersecò le righe \(1808\) volte. Quindi Lazzarini ottenne un valore approssimato

\[ \pi \approx 3,141592 \]

Questo metodo di calcolo di \(\pi\) è considerato uno dei precursori del Monte Carlo, importante metodo di simulazione per risolvere problemi complessi. Il metodo Monte Carlo è stato ad esempio usato dagli scienziati nella metà degli anni ’40 nel campo della fisica nucleare, nell’ambito del Progetto Manhattan per la costruzione della bomba atomica.
Esso può anche essere utilizzato per il calcolo di integrali complessi, che non si riescono a risolvere con i metodi elementari.

Esercizio 4.1
Su un cerchio di raggio \(R\) tracciamo delle corde parallele ad una data direzione. Supponiamo che i punti di intersezione delle corde con il diametro perpendicolare siano ugualmente probabili. Calcolare la probabilità che la lunghezza di una corda scelta a caso non superi \(R\).
Soluzione: \(\left[p = 1 – \frac{\sqrt{3}}{2}\right]\)

Esercizio 4.2
Siano dati due numeri casuali scelti nell’intervallo \([0,1]\). Calcolare la probabilità che la loro somma non superi \(1\) e il loro prodotto sia al massimo \(3/16\).

Suggerimento
Il problema si può risolvere per via geometrica, calcolando il rapporto fra l’area favorevole e l’area totale del seguente diagramma.

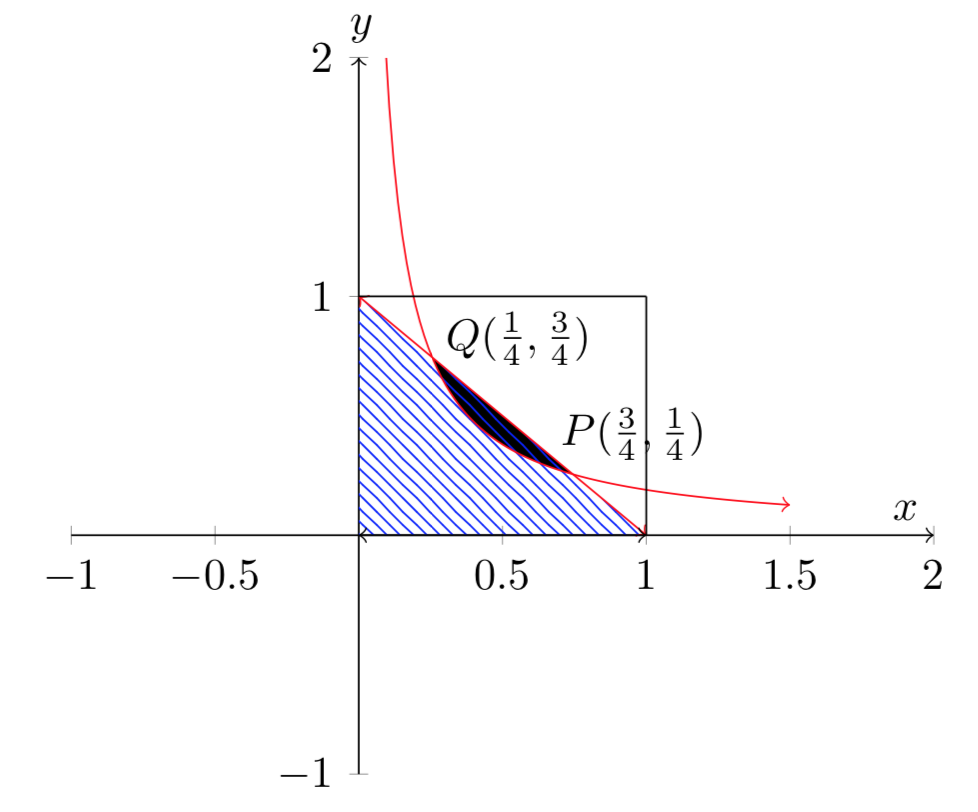
Soluzione: \(\left[p=\frac{1}{4}+\frac{3}{16}\ln 3\right]\)

5) La concezione frequentista della probabilità

La definizione classica di probabilità si è dimostrata molto utile nel campo dei giochi d’azzardo e di altre situazioni semplici da modellare. Tuttavia ha dei limiti fondamentali se applicata allo studio dei fenomeni complessi della fisica, della tecnologia e delle scienze umane. Ad esempio non è utile per calcolare la probabilità che un particolare atomo di una sostanza radioattiva decada entro un certo intervallo di tempo, oppure per determinare la percentuale di votanti in una elezione politica, o per determinare la probabilità che un bambino che sta per nascere sia maschio o femmina.
La concezione frequentista è stata sviluppata da diversi matematici, tra i quali Bolzano (1781-1841), Richard von Mises (1883-1953) e Fisher (1890-1962).

5.1) Frequentismo finito

La concezione frequentista definisce la probabilità mediante il concetto di frequenza relativa di un evento, osservata in una serie molto ampia di esperimenti. La base di questa definizione dipende dall’osservazione che in molti fenomeni in cui si effettuano esperimenti ripetuti, mantenendo invariate le condizioni al contorno, il rapporto fra il numero dei casi in cui un dato evento si verifica e il numero totale delle prove tende ad assumere un valore abbastanza stabile.

Esempio 5.1
Lanciando una moneta non truccata un grande numero di volte, ad esempio \(1000\), si nota che il rapporto fra il numero dei casi in cui esce ad esempio testa e il numero totale dei lanci, tende a stabilizzarsi intorno al \(50\%\). Secondo la concezione frequentista in questo esperimento la probabilità che esca testa è il valore limite di questo rapporto, all’aumentare del numero dei lanci.
In pratica normalmente non è possibile realizzare un numero molto grande di esperimenti, quindi la probabilità viene calcolata sui dati che si hanno a disposizione con un numero finito di prove sufficientemente grande. Supponendo quindi di fare \(n\) prove di un esperimento, in cui l’evento \(A\) si verifica un numero \(n_{A}\) di volte, la probabilità dell’evento \(A\) è così definita:

\[ P(A) = \frac{n_{A}}{n} \ , \quad n \text{ finito} \]

Nell’approccio frequentista quindi la probabilità viene calcolata a posteriori, dopo avere eseguito un certo numero di prove ripetute di un esperimento casuale. Nell’approccio classico invece la probabilità è calcolata a priori, senza la necessità di eseguire delle prove.
Una connessione tra queste due concezioni è possibile grazie alla legge dei grandi numeri, la quale afferma che sotto opportune condizioni le frequenze convergono alla probabilità.
Un problema immediato con la definizione frequentista è il cosiddetto problema del caso singolo, cioè non si applica a eventi individuali. Ad esempio lanciando una moneta una sola volta, la frequenza dei valori testa e croce può assumere solo i valori \(0,1\). Nella realtà molti esperimenti non rientrano nello schema della definizione frequentista e non sono ripetibili; ad esempio il risultato di una partita di calcio, l’elezione di un Presidente della Repubblica, ecc.

5.2) Frequentismo infinito

In termini matematici la concezione frequentista definisce la probabilità di un evento \(A\) come il valore limite della frequenza relativa con la quale appare in un numero grande di prove nelle stesse condizioni. La definizione di von Mises per la probabilità di un evento \(A\), è la seguente:

\[ p(A) = \lim_{n \to \infty}\frac{n_{A}}{n} \]

dove \(n_{A}\) è il numero dei casi in cui l’evento \(A\) si verifica e \(n\) è il numero totale delle prove.
L’utilizzo del concetto di limite di una successione in questa definizione richiede dei chiarimenti. Il simbolo di limite usato nella definizione non deve essere confuso con il simbolo matematico di limite, utilizzato nel calcolo differenziale. In realtà non c’è alcuna garanzia che la successione delle frequenze tenda ad un limite, secondo la definizione matematica.
Per dare una giustificazione rigorosa von Mises assume l’esistenza di infinite successioni di esperimenti o prove, che chiama collettivi. Quindi assume che ogni collettivo soddisfi i seguenti assiomi:

• assioma di convergenza: si assume l’esistenza del limite della frequenza relativa di ogni evento;  
• assioma del disordine: la frequenza limite di ogni evento o attributo in un collettivo è la stessa in ogni successione infinita.

La probabilità di un evento, nel corso di una particolare prova, è la frequenza relativa all’occorrenza di quel evento in un collettivo.
Quindi secondo questa concezione è necessaria una sequenza infinita di prove per definire le probabilità. Tuttavia nella realtà non è possibile effettuare una sequenza infinita di esperimenti. Nella pratica infatti si assume di definire la probabilità come il valore della frequenza dei successi su un numero di prove sufficientemente grande.
Notiamo che nei casi in cui si può applicare la definizione classica di probabilità, la frequenza relativa assume valori vicini alla probabilità \(p\) dell’evento, calcolata nel modo classico. Ad esempio lanciando una moneta \(1000\) volte la frequenza di testa tende al valore teorico della probabilità classica, cioè al \(50\%\).
La definizione frequentista trova applicazione in diversi campi delle scienze sociali ed economiche. Ad esempio per le assicurazioni sulla vita è importante conoscere la probabilità che una persona raggiunga una certa età, ad esempio \(80\) anni. In questo caso si utilizzano le tavole di mortalità costruite sulla base di archivi storici, che permettono di valutare le probabilità con un certo grado di fiducia.

5.3) Osservazioni sulla definizione frequentista

La definizione frequentista si può teoricamente applicare soltanto agli esperimenti ripetibili, nei quali il limite della frequenza tende a stabilizzarsi all’aumentare del numero delle prove. Chiaramente nella realtà ci sono molte situazioni nelle quali questa definizione non è applicabile: il tempo atmosferico in un giorno futuro, il risultato di un partite di calcio, il risultato di una votazione elettorale, ecc.
Anche nel caso di esperimenti ripetibili non è sempre possibile avere le stesse condizioni al contorno. Possono esserci variazioni che influiscono sul risultato.
Inoltre in molti casi la frequenza di un evento non raggiunge mai una valore stabile, ma esistono delle fluttuazioni infinite.

6) La concezione soggettivista della probabilità

Abbiamo visto che sia la definizione classica sia la definizione frequentista, nonostante la loro applicabilità e utilità in molti settori, hanno dei limiti teorici che è impossibile superare.
La teoria soggettivista della probabilità è dovuta principalmente a De Finetti (1906-1985) e Ramsey (1903-1930). Secondo De Finetti la probabilità non ha un significato oggettivo, ma esiste sono in relazione allo stato soggettivo di un individuo.

“La probabilità non esiste”.

De Finetti (Teoria delle probabilità – Vol. 1)

Nella concezione soggettivista la probabilità viene definita come misura del grado di fiducia di un soggetto determinato nell’avverarsi di un evento. Per definirla in modo concreto, De Finetti utilizza il linguaggio delle scommesse. Supponiamo che un individuo voglia accettare una scommessa, basata sul verificarsi d’un dato evento. La probabilità di un evento \(A\) per un certo soggetto è un numero reale \(p\), che rappresenta il valore che il soggetto è disposto a pagare per avere un euro in caso di verificarsi dell’evento.
De Finetti riprende i concetto di valore atteso di una variabile aleatoria, già introdotto da Pascal e Huygens. All’evento \(A\) possiamo associare la variabile aleatoria \(\chi_{A}\), funzione caratteristica dell’evento stesso, che assume i valori seguenti:

\[ \begin{array}{l} \chi_{A}(x)=1 \ , \quad \text{ se } x \in A \\ \chi_{A}(x)=0 \ , \quad \text{ se } x \not\in A \\ \end{array} \]

La probabilità P(A) di un evento A è definita come il valore atteso della variabile aleatoria \(\chi_{A}\), cioè

\[ P(A) = E(\chi_{A}) \]

Esempio 6.1
Supponiamo \(p=0,2\). Allora il soggetto accetterà di pagare una quota di \(20\) se c’è un premio di \(100\). Oppure invertendo i ruoli di promettere una vincita di \(100\) a chi è disposto a pagare una quota di scommessa di \(20\).

Nella definizione di De Finetti si assume che nella scommessa si è disposti ad assumere indifferentemente il ruolo dello scommettitore o del banco, cioè a scommettere sul verificarsi dell’evento \(E\), o sul verificarsi del suo complementare \(\overline{E}\). Questo implica che le valutazioni soggettive non possono essere arbitrarie, ma si devono rispettare delle regole di coerenza.
La regola fondamentale di coerenza impone che le probabilità degli eventi non permettono a nessuno scommettitore o al banco di vincere con certezza.
Supponiamo che una scommessa consista nel pagare \(q\) per avere il valore aleatorio \(X\). Allora \((X – q)\) è il guadagno dello scommettitore e \((q-X)\) è il guadagno del banco. La regola di coerenza impone che \(X-q\) non può essere positivo o negativo con certezza, altrimenti nessuno sarebbe disposto a scommettere o a fungere da banco.

La condizione di coerenza è illustrata dal seguente teorema:

Teorema 6.1 – De Finetti
Condizione necessaria e sufficiente per la coerenza è che la funzione \(P(E)\), cioè la probabilità assegnata ad un evento \(E\), goda delle seguenti proprietà:

\[ \begin{array}{l} 0 \le P(E) \le 1 \ , \quad \text{per ogni evento E}\\ P(E) = 1 \ , \quad \quad \text{se E è certo} \\ P(E)= 0 \ , \quad \quad \text{se E è impossibile} \\ P(E_{1} \cup E_{2})=P(E_{1})+ P(E_{2}) \ , \quad \text{se i due eventi sono incompatibili} \end{array} \]

6.1) Osservazioni sulla definizione soggettivista

La concezione soggettivista ha assunto un ruolo importante in molti campi, in particolare nelle scienze sociali e del comportamento umano. Un punto forte di questa teoria è che permette di ampliare il campo di applicabilità della probabilità, anche ad eventi singoli non ripetibili.
Tuttavia la teoria è soggetta a molte critiche, in quanto viene considerata incapace di assegnare un significato oggettivo alle probabilità, come in genere avviene per le grandezze che si utilizzano nelle scienze fisiche e matematiche. Nella concezione classica e nella concezione frequentista le probabilità sono valutate in base a proprietà intrinseche dell’esperimento.
Tuttavia ricordiamo che soggettivismo non significa che le valutazioni siano arbitrarie. In primo luogo anche nella teoria soggettivista si devono rispettare le regole di coerenza. Inoltre le valutazioni soggettive sono in realtà determinate dagli stessi ragionamenti utilizzati nella probabilità classica e frequentista, nel caso in cui queste si possano applicare.
Per approfondire la teoria soggettivista vedere il testo di de Finetti ^[2].

7) Assiomatizzazione di Kolmogorov

I matematici russi hanno dato un contributo fondamentale allo sviluppo della teoria della probabilità. Tra i nomi più importanti ricordiamo Chebyshev, Markov e Kolmogorov. Kolmogorov è stato uno dei matematici più importanti del secolo XX. I suoi contributi spaziano su molti settori della scienza e della matematica (teoria della misura e dell’integrazione, teoria della probabilità, teoria degli algoritmi, analisi di Fourier, sistemi dinamici, soluzione del problema XIII di Hilbert, e molti altri).
Come è noto, nella matematica moderna gli assiomi sono delle proposizioni che vengono considerate vere in una data teoria. A partire da questi assiomi vengono dimostrati i vari teoremi della teoria, utilizzando le regole della logica.
Nel \(1933\) Kolmogorov ha proposto una definizione assiomatica della teoria della probabilità, rinunciando al tentativo di dare un particolare significato al concetto di probabilità di un evento, ma definendo gli assiomi che deve soddisfare la funzione di probabilità.
All’inizio del suo testo del \(1933\), pubblicato in tedesco, ‘Grundbegriffe der Wahrscheinlichkeitsrechnung’ (Fondamenti di teoria della probabilità ^[1]), Kolmogorov espone la sua strategia:

“La teoria delle probabilità come disciplina matematica può e dovrebbe essere sviluppata a partire da assiomi, nello stesso modo della geometria o dell’algebra”

Andrei Kolmogorov

Kolmogorov ha definito gli assiomi per la teoria della probabilità all’interno della teoria della misura, cioè la teoria utilizzata nell’analisi matematica per definire e calcolare la misura di oggetti di varie dimensioni, come lunghezze, aree, volumi.
Prima di illustrare gli assiomi di Kolmogorov, introduciamo il concetto di algebra e \(\sigma\)-algebra di insiemi.

7.1) Algebra e sigma-algebra di insiemi

Sia \(\Omega\) un insieme qualsiasi senza una speciale struttura. Una collezione \(\mathfrak{F}\) di sottoinsiemi di \(\Omega\) si dice che è un’algebra di insiemi se valgono le seguenti proprietà:

\[ \begin{array}{l} \emptyset \in \mathfrak{F} \quad \text{e} \quad \Omega \in \mathfrak{F} \\ A \in \mathfrak{F} \implies \overline{A} \in \mathfrak{F}\\ A_{1},A_{2}, \cdots,A_{n} \in \mathfrak{F} \implies \bigcup_{i=1}^{n}{A_{i}} \in \mathfrak{F} \\ A_{1},A_{2}, \cdots,A_{n} \in \mathfrak{F} \implies \bigcap_{i=1}^{n}{A_{i}} \in \mathfrak{F} \\ \end{array} \]

Le ultime due proprietà affermano che un algebra di insiemi è una collezione chiusa rispetto alle operazioni di unione e intersezione finita di insiemi.
L’approccio di Kolmogorov consiste nel partire da un insieme \(\Omega\) di eventi elementari. Quindi considerare una famiglia \(\mathfrak{F}\) di sottoinsiemi di \(\Omega\), chiamati eventi casuali. La famiglia \(\mathfrak{F}\) non può essere arbitraria, ma deve essere un’algebra di sottoinsiemi di \(\Omega\).
In alcune situazioni è necessario estendere la proprietà di chiusura a famiglie infinite numerabili di insiemi. Allora abbiamo una \(\sigma \)-algebra di insiemi:

\[ \begin{array}{l} A_{1},A_{2}, \cdots,A_{n},\cdots \in \mathfrak{F} \implies \bigcup_{i=1}^{\infty}{A_{i}} \in \mathfrak{F} \\ A_{1},A_{2}, \cdots,A_{n},\cdots \in \mathfrak{F} \implies \bigcap_{i=1}^{\infty}{A_{i}} \in \mathfrak{F} \\ \end{array} \]

Useremo il termine \(\sigma \)-algebra in entrambi i casi, finito o infinito.

Esempio 7.1
Supponiamo di lanciare un dado con \(6\) facce. L’insieme degli eventi elementari è il seguente

\[ \Omega =\{E_{1},E_{2},\cdots,E_{6}\} \]

dove \(E_{k}\) è l’evento corrispondente all’uscita del numero \(k\) del dado.
Gli eventi casuali sono costituiti dalla collezione \(\mathfrak{F}\) dei \(64\) sottoinsiemi di \(\Omega\), compreso il sottoinsieme vuoto.

Esempio 7.2
Consideriamo il lancio di due monete. Allora abbiamo

\[ \Omega=\{(T,T),(T,C),(C,T),(C,C)\} \]

e una \(\sigma\)-algebra è la seguente:

\[ \mathfrak{F}=\{\emptyset,(T,T),(T,C),(C,T),(C,C),\Omega\} \]

7.2) Assiomi di Kolmogorov

Il modello matematico di Kolmogorov su cui costruire la teoria della probabilità è costituito da una terna di elementi \((\Omega,\mathfrak{F},P)\), chiamata spazio di probabilità:

\[ \begin{array}{l} \Omega : \quad \text{ spazio degli eventi elementari}\\ \mathfrak{F} : \quad \sigma \text{-algebra di eventi} \\ P: \mathfrak{F} \to [0,1] : \quad \text{funzione di probabilità} \end{array} \]

L’insieme \(\Omega\) è lo spazio degli eventi elementari e rappresenta l’insieme di tutti i possibili risultati dell’esperimento. La \(\sigma\)-algebra \(\mathfrak{F}\) contiene gli eventi collegati all’esperimento. La funzione probabilità \(P: \mathfrak{F} \to [0,1]\) è definita sugli eventi casuali e soddisfa i seguenti assiomi:

\[ \begin{array}{l} P(\Omega)=1 \\ P(\emptyset)=0 \\ P\left(\bigcup_{k} A_{k}\right)=\sum_{k}P(A_{k}) \end{array} \]

dove nel terzo assioma gli eventi \(A_{k}\) sono incompatibili a coppie.
Notiamo che la funzione probabilità di Kolmogorov è definita solo per gli eventi della \(\sigma\)-algebra, mentre non è definita per i sottoinsiemi di \(\Omega\) non appartamenti alla \(\sigma\)-algebra.
A partire dagli assiomi di Kolmogorov viene costruita tutta la teoria della probabilità, in modo simile alle altre branche della matematica, come ad esempio la geometria euclidea, costruita a partire dagli assiomi di Euclide.
Oltre al concetto di spazio di probabilità \((\Omega,\mathfrak{F},P)\), Kolmogorov ha definito anche il concetto fondamentale di variabile aleatoria, cioè una grandezza il cui valore è determinato da un esperimento casuale.
Precisamente una variabile aleatoria è una funzione a valori reali \(X\) misurabile, definita sullo spazio campionario \(\Omega\)

\[ X: \Omega \to \mathbb{R} \]

Il concetto di funzione misurabile è definito nella teoria della misura dell’analisi matematica. In termini semplici significa che per ogni numero reale \(x\) l’insieme

\[ E_{x}=\{\omega \in \Omega: X(\omega) \lt x\} \]

appartiene alla \(\sigma\)-algebra \(\mathfrak{F}\).

Esempio 7.3
Supponiamo di avere un’urna con \(4\) palline nere, numerate \(1,2,3,4\) e \(2\) palline bianche numerate \(5,6\). Facciamo una estrazione casuale di due palline, senza restituzione. Lo spazio degli eventi elementari è \(\Omega=\{(1,2),(2,1), \cdots, (5,6),(6,5)\}\). Indichiamo con \(X\) la variabile aleatoria che conta il numero delle palline nere estratte. I valori possibili sono \(X=0,1,2\). Ad esempio

\[ \begin{array}{l} X(\omega)= 0 \ , \quad \text{se } \omega=(5,6) \text{ oppure } \omega=(6,5) \end{array} \]

Per comprendere il testo di Kolmogorov e quindi la moderna teoria della probabilità è importante conoscere i concetti fondamentali della teoria della misura. Un testo eccellente è ad esempio ^[5].

8) Probabilità condizionata e teorema di Bayes

Un concetto fondamentale nella teoria della probabilità è quello della dipendenza fra eventi. Due eventi sono indipendenti se il verificarsi dell’uno non influisce sulla probabilità del verificarsi dell’altro. Altrimenti si dicono dipendenti.
In molte situazioni nei giochi d’azzardo le successive prove di esperimenti casuali sono indipendenti: lancio di dadi, gioco alla roulette, estrazione del lotto, ecc. In altre situazioni invece le prove non sono indipendenti: estrazione di palline senza reimmissione nell’urna, black-jack, ecc.
L’indipendenza delle prove successive in molti giochi d’azzardo non è compresa bene da molti giocatori. Ad esempio nel gioco del lotto molti giocatori tendono a puntare sui numeri ritardatari, cioè i numeri che non escono da molto tempo. Tuttavia questa è una illusione, poche le varie estrazioni del lotto sono indipendenti e non hanno memoria.
In termini matematici se due eventi \(A,B\) sono indipendenti allora

\[ P(A \cap B)= P(A)P(B) \]

Se due eventi sono dipendenti, si definisce la probabilità condizionata di \(A\) dato il verificarsi di \(B\) il seguente valore:

\[ P(A|B) = \frac {P(A \cap B)}{P(B)} \]

Il significato della probabilità condizionata è che lo stato di informazione può cambiare le probabilità. Il fatto di sapere che un evento \(B\) si è verificato, può influire sulla nostra valutazione della probabilità dell’evento \(A\).

Esempio 8.1
Nel gioco del poker, supponiamo che un giocatore abbia ricevuto \(4\) carte di un colore e la quinta carta di un colore diverso. Supponiamo che decida di scartare la carta di colore diverso e chiedere una nuova carta.
Calcolare la probabilità che realizzi il punteggio di colore.
Risposta: \(\left[p= \dfrac{9}{47}\right]\)

Il concetto di probabilità condizionata è previsto nelle varie definizioni di probabilità. In realtà ogni probabilità che viene calcolata è una probabilità condizionata, in quanto dipende dalla spazio campionario preso come base degli eventi, che corrisponde allo stato di informazione disponibile.

È facile dimostrare il seguente importante teorema:

Teorema 8.1 – Legge delle probabilità totali
Supponiamo che gli eventi \(B_{1},B_{2}, \cdots,B_{n}\) costituiscano una partizione dello spazio campionario \(\Omega\), cioè siano disgiunti, cioè incompatibili fra loro, e inoltre

\[ \Omega = B_{1} \cup B_{2} \cup \cdots \cup B_{n} \]

Allora risulta

\[ \begin{array}{l} P(A) = \sum\limits_{k=1}^{n}P(A|B_{k})P(B_{k}) \end{array} \]

8.1) Probabilità a priori e a posteriori

A volte un determinato evento \(A\) non può essere osservato direttamente, ma se \(A\) è in qualche modo legato ad un secondo evento \(B\), che invece possiamo osservare, la probabilità condizionata \(P(A|B)\) prende il nome di probabilità a posteriori, poiché indica un valore di probabilità valutato dopo la conoscenza di \(B\). Viceversa, in tale contesto la probabilità \(P(A)\) viene chiamata probabilità a priori, cioè senza avere l’informazione dell’evento \(B\).
Dalla definizione di probabilità condizionata segue la formula di Bayes:

\[ P(A|B) = \frac {P(B|A)P(A)}{P(B)} \]

Mettendo insieme la legge delle probabilità totali con la definizione di probabilità condizionata abbiamo il seguente teorema:

Teorema 8.2 – Regola di Bayes

\[ \begin{array}{l} P(B_{k}|A) = \dfrac{P(A|B_{k})P(B_{k})}{\sum\limits_{k=1}^{n}P(A|B_{k})P(B_{k})} \end{array} \]

Nella regola di Bayes abbiamo:

• \(P(B_{k}|A)\) è la probabilità a posteriori dell’ipotesi \(B_{k}\)
• \(P(B_{k})\) è la probabilità a priori dell’ipotesi \(B_{k}\)
• \(P(A|B_{k})\) è la verosimiglianza dell’evento \(A\)

La regola di Bayes si applica quando un evento \(A\) può verificarsi sotto diverse condizioni o ipotesi, rappresentate dagli eventi disgiunti \(B_{1},B_{2},\cdots,B_{n}\). Supponiamo di conoscere inizialmente le probabilità degli eventi \(B_{k}\). Supponiamo inoltre di conoscere le probabilità condizionate \(P(A|B_{k})\). Una volta effettuato l’esperimento la formula di Bayes permette di fare una nuova valutazione delle singole ipotesi \(P(B_{k}|A)\).

Esercizio 8.1
In un piccolo paese il \(51\%\) degli adulti è femmina e il \(49\%\) è maschio. Si sceglie a caso una persona per una intervista. Calcolare la probabilità a priori che sia femmina.
Viene in seguito comunicato che la persona scelta è un fumatore. Supponiamo che il 10% delle femmine fumi sigarette, contrariamente al 5% dei maschi.
Calcolare nuovamente la probabilità che il soggetto scelto sia femmina.

Per un studio approfondito del moderno calcolo delle probabilità si può consultare il testo di Ross ^[6].

9) Esercizi proposti

Esercizio 9.1
Un’urna contiene \(n\) palline, di cui \(n_{b}\) bianche e \(n_{r}\) rosse. Supponiamo di estrarre \(2\) palline con restituzione. Quale è la probabilità \(p_{1}\) che la prima pallina sia rossa, la probabilità \(p_{2}\) che la seconda pallina sia rossa, la probabilità \(p_{3}\) che entrambe le palline siano rosse?

Soluzione: \(\left[ p_{1}=p_{2}=\dfrac{n_{r}}{n};p_{3}=\left(\dfrac{n_{r}}{n}\right)^{2}\right]\)

Esercizio 9.2
Risolvere l’esercizio precedente nell’ipotesi di estrazione senza restituzione.

Soluzione: \(\left[p_{1}=p_{2}=\dfrac{n_{r}}{n};p_{3}=\left(\dfrac{n_{r}(n_{r}-1)}{n(n-1)}\right)\right]\)

Esercizio 9.3
Sia data un’urna contenente \(M\) palline, numerate da \(1\) ad \(M\). Supponiamo di estrarre con restituzione un campione di dimensione \(n\). Calcolare la probabilità che non ci siano ripetizioni nel campione.

Soluzione: \(\left[p = \frac{M(M-1) \cdots (M-n+1)}{M^{n}}\right]\)

Esercizio 9.4
Supponiamo che \(n\) persone siano in una stanza. Calcolare la probabilità \(p_{1}\) che non si trovino nella stanza due persone il cui compleanno cade nello stesso giorno. Considerare tutti gli anni di \(365\) giorni.
Dimostrare quindi che, affinché la probabilità \(p_{2}\) che ci siano due persone con lo stesso compleanno sia maggiore di \(\dfrac{1}{2}\), ci devono essere almeno \(23\) persone nella stanza.

Suggerimento
La prima parte è un caso particolare dell’esercizio precedente. Abbiamo quindi

\[ p_{1} = \frac{365 \cdot 364 \cdots (365-n+1)}{365^{n}} \]

Per la seconda parte la probabilità che ci siano almeno due persone con lo stesso compleanno è

\[ p_{2} = 1-p_{1}= 1 – \frac{365 \cdot 364 \cdots (365-n+1)}{365^{n}} \]

Bisogna quindi determinare il valore minimo di \(n\) tale che \( p_{2} \ge \frac{1}{2}\). Per effettuare i calcoli si può utilizzare la formula di Stirling che approssima il valore del fattoriale:

\[ n! \approx \sqrt{2 \pi n} \left(\frac{n}{e}\right)^{n} \]

Facendo i calcoli si trova per \(n=23\) il valore \(p_{1} \approx 0,4927\) e quindi \(p_{2}=1-p_{1} \approx 0,5073\).

Esercizio 9.5 – Estrazione con restituzione
Una urna contiene \(M\) palline di cui \(M_{B}\) bianche e \(M_{R}\) rosse. Viene estratto con restituzione un campione di dimensione \(n\), con \(0 \le n \le M\). Sia \(k\) un intero compreso fra \(0\) e \(n\).
Indichiamo con \(p=\frac{M_{B}}{M}\) la frazione delle palline bianche.
Dimostrare che la probabilità dell’evento \(S_{k}\) che vengano estratte esattamente \(k\) palline bianche è

\[ P(S_{k})= \binom{n}{k}p^{k}(1-p)^{n-k} \]

Questa funzione è la famosa distribuzione di Bernoulli. In genere si utilizza l’espressione probabilità che ci siano \(k\) successi su \(n\) prove. Chiaramente si adatta a numerose situazioni.

Esercizio 9.6 – Estrazione senza restituzione
Una urna contiene \(M\) palline di cui \(M_{B}\) bianche e \(M_{R}\) rosse. Viene estratto senza restituzione un campione di dimensione \(n\), con \(0 \le n \le M\). Sia \(k\) un intero compreso fra \(0\) e \(n\).
Dimostrare che la probabilità dell’evento \(S_{k}\) che vengano estratte esattamente \(k\) palline bianche è

\[ P(S_{k})= \frac{\binom{M_{B}}{k} \binom{M_{R}}{n-k}}{\binom{M}{n}} \]

Questa funzione è la distribuzione ipergeometrica.

Esercizio 9.7 – Statistica di Maxwell-Boltzmann
Supponiamo di avere \(r\) particelle distinguibili distribuite su \(n\) celle. Nella statistica di Maxwell-Boltzmann, valida nella fisica classica, tutte le \(n^{r}\) configurazioni sono ugualmente probabili. Dimostrare che la probabilità che le celle \(1,2,\cdots,n\) contengano \(r_{1},r_{2},\cdots,r_{n}\) particelle rispettivamente, dove \(r_{1}+r_{2}+ \cdots + r_{n}=r\), è

\[ \frac{r!}{r_{1}!r_{2}!\cdots r_{n}|}n^{-r } \]

Esercizio 9.8 – Statistica di Bose-Einstein
Supponiamo di avere \(r\) particelle indistinguibili distribuite su \(n\) celle. La statistica di Bose-Einstein si applica alle particelle con spin intero, come i fotoni, che non seguono il principio di esclusione di Pauli.
Quindi non c’è limite al numero di particelle che possono stare in una cella. Il numero di configurazioni distinguibili è dato dal numero di combinazioni con ripetizione di \(n\) oggetti presi a gruppi di \(r\), cioè:

\[ X_{r,n}=\binom{n+r-1}{r}=\binom{n+r-1}{n-1} \]

Ogni configurazione ha probabilità \(p=X_{r,n}^{-1}\).

Esercizio 9.9 – Statistica di Fermi-Dirac
Supponiamo di avere \(r\) particelle indistinguibili distribuite su \(n\) celle. La statistica di Fermi-Dirac si applica alle particelle con spin non intero, come gli elettroni, che seguono il principio di esclusione di Pauli.
Quindi in ogni cella ci può essere al massimo una particella. Il numero di configurazioni distinguibili è dato dal numero di combinazioni semplici di \(n\) oggetti presi a gruppi di \(r\), cioè:

\[ X_{r,n}=\binom{n}{r} \]

dove \(r_{k}=0,1\).
Ogni configurazione ha probabilità \(p=X_{r,n}^{-1}\).

Conclusione

Il processo di sviluppo della teoria della probabilità è simile a quanto successo con altre branche della matematica, come la geometria e l’algebra. Inizialmente si ha uno sviluppo di risultati, in apparenza scollegati, che trovano comunque applicazioni in vari campi. Una volta raggiunto un livello di maturità sufficiente, viene formulata una definizione assiomatica, che permette di avere una comprensione più chiara e completa della teoria matematica in esame.
La formulazione assiomatica di Kolmogorov è il risultato finale dello sviluppo della teoria della probabilità, iniziato con Cardano, Pascal e Fermat, e poi ampliato da Bernoulli, Laplace, Chebyshev, Poisson, e molti altri.
Sostanzialmente Kolmogorov ha dato una sistemazione logica e chiara ai risultati ottenuti nei secoli precedenti. A partire dagli assiomi di Kolmogorov, lo sviluppo dei teoremi della teoria della probabilità si basa solo sulla correttezza logica, indipendentemente da eventuali applicazioni nel mondo fisico.

---

Bibliografia

^[1]A. N. Kolmogorov – Foundations of the Theory of Probability (Dover)

^[2]Bruno de Finetti – Theory of Probability (Vol. I,II – Wiley)

^[3]Bruno de Finetti – Filosofia della Probabilità (Il Saggiatore)

^[4]W. Feller – An Introduction to Probability Theory (Vol. I – Wiley)

^[5]Kolmogorov, Fomin – Elementi di Teoria delle Funzioni e di Analisi Funzionale (Editori Riuniti)

^[6]S. Ross – A First Course in Probability (Pearson)