Consideriamo una regione limitata dello spazio euclideo a \(n\) dimensioni \(\mathbb{R}^{n}=\{(x_{1},x_{2}, \cdots,x_{n}): x_{k} \in \mathbb{R}\}\). La geometria dei numeri studia i punti con coordinate cartesiane intere che sono contenuti nella regione. Ad esempio nello spazio \(\mathbb{R}^{3}\) si contano i punti \((x,y,z)\) a coordinate intere contenuti in una sfera di raggio \(R\), oppure nel piano \(\mathbb{R}^{2}\) i punti interi contenuti in una curva.
In questo articolo studieremo il classico problema del cerchio di Gauss, che consiste nel determinare i punti interi del piano contenuti in un cerchio, con centro nell’origine del sistema di coordinate.
1) Il caso semplice unidimensionale
Indichiamo con \(N_{1a}(t)\) il numero degli interi \(x\) che soddisfano la seguente disequazione:
\[ x^{2} \le t \ , \quad x \in \mathbb{Z}, \ t \in \mathbb{R} \]Il problema consiste nel determinare i numeri interi compresi nell’intervallo \([-\sqrt{t},\sqrt{t}]\).
Esempio 1.1
Supponiamo \(x^{2} \le 101\). Gli interi che soddisfano la disequazione sono \(0, \pm 1, \cdots, \pm 10\). Quindi \(N_{1a}(101)=21\).
Esercizio 1.1
Dimostrare che
dove il simbolo \(\lfloor x \rfloor\) indica il più grande intero che è minore od uguale a \(x\).
Consideriamo ora una variante del problema. Determinare il numero \(N_{1b}(t)\) di soluzioni intere che soddisfano la seguente disequazione:
Esempio 1.2
Supponiamo \(|x| \le 10\pi\).
Gli interi che soddisfano la disequazione sono \(0, \pm 1, \cdots, \pm 31\). Quindi \(N_{1b}(10\pi)=63\).
Esercizio 1.2
Dimostrare che
2) Il numero di rappresentazioni di un intero come somma di due quadrati
Il problema del cerchio di Gauss consiste nel determinare il numero di punti a coordinate intere, compresi in un cerchio di raggio \(r\) e con centro nel punto \((0,0)\). In termini algebrici il problema di Gauss consiste nella ricerca del numero di soluzioni intere della disequazione seguente:
\[ x^{2}+y^{2} \le r^{2} \ , \quad x,y \in \mathbb{Z} \]Il problema del cerchio di Gauss è strettamente collegato con il classico problema di determinare le rappresentazioni di un intero positivo \(n\) come somma di due quadrati di interi.
Ricordiamo alcuni risultati fondamentali. Per approfondire vedere articolo su questo sito.
Definizione 2.1
Un intero positivo \(n\) ha un rappresentazione come somma di due quadrati interi se
Anche il numero zero è ammesso tra i valori da \(a,b\). Ad esempio
\[ \begin{array}{l} 17 = 4^{2}+ 1^{2} \\ 50 = 5^{2}+ 5^{2} \\ 16 = 4^{2} + 0^{2} \\ 25= 5^{2}+0^{2}=3^{2}+4^{2}\\ \end{array} \]2.1) Numeri primi somma di due quadrati
Consideriamo il caso semplice in cui un intero è un numero primo. Per il numero primo \(2\) abbiamo \(2=1^{2}+1^{2}\). Per gli altri numeri primi abbiamo il seguente teorema:
Teorema 2.1 – Eulero-Fermat
Un numero primo \(p\) dispari può essere espresso come somma di due quadrati se e solo se \(p \equiv 1 \pmod{4}\). In simboli
Osserviamo che un numero primo dispari \(p\) può essere solo del tipo \(p=4k+1\) oppure \(p=4k+3\), con \(k\) intero.
Il quadrato di un numero pari è divisibile per \(4\), mentre il quadrato di un numero dispari è congruente a \(1 \pmod {4}\), cioè il resto della divisione per \(4\) è uguale a \(1\). Quindi la somma di due quadrati può avere resto uguale a \(0,1,2\) ma non \(3\) nella divisione per \(4\). Da ciò deriva che un primo della forma \(p=4k+3\) non può essere espresso come somma di due quadrati.
Quindi se un numero \(p\) è dispari e risulta \(p=x^{2} + y^{2}\), allora \(p\) deve essere necessariamente del tipo \(p=4k+1\).
Il teorema di Eulero-Fermat afferma che la condizione è anche sufficiente.
2.2) Numeri composti somma di due quadrati
Consideriamo ora gli interi composti. La soluzione di questo problema è contenuta nel seguente teorema:
Teorema 2.2
Sia dato un intero positivo \(n\) con la seguente scomposizione in fattori primi:
dove \(p_{i} \equiv 1 \pmod{4}\) e \(q_{j} \equiv 3 \pmod{4}\). Allora è possibile scrivere \(n=x^{2}+ y^{2}\) se e solo se tutti gli esponenti \(s_{j}\) sono pari.
2.3) Numero di rappresentazioni come somma di due quadrati
Definizione 2.2 – La funzione aritmetica \(r_{2}(n)\)
Definiamo la funzione aritmetica \(r_{2}(n)\) come il numero delle rappresentazioni di \(n\) nella forma
Si contano come diverse le rappresentazioni che differiscono per i segni o per l’ordine, ed è ammesso anche lo zero. Alcuni esempi sono i seguenti:
\[ \begin{array}{l} 0 = 0^{2} +0^{2} \implies r_{2}(0)=1 \\ 1 = (\pm 1)^{2}+ 0^{2}=0^{2} + (\pm 1)^{2} \implies r_{2}(1)=4 \\ 2= (\pm 1)^{2}+ (\pm 1)^{2} \implies r_{2}(2)=4 \end{array} \]Esercizio 2.1
Dimostrare le seguenti formule:
Dai teoremi precedenti segue il seguente risultato:
Teorema 2.3
Se \(p\) è un primo del tipo \(4k+1\), allora \(r_{2}(p)=8\). La rappresentazione è di fatto unica; le altre sono diverse solo per l’ordine e per i segni.
Se \(n\) è un intero positivo del tipo \(4k+3\), allora \(r_{2}(n)=0\) .
Vogliamo ora determinare un’espressione utile per il calcolo dei valori di \(r_{2}(n)\). Sia \(n=p_{1}^{a_{1}} \cdots p_{k}^{a_{k}}\) la fattorizzazione di un intero positivo. Ricordiamo che il numero dei divisori di \(n\), indicato con \(d(n)\), è dato dalla seguente formula
\[ d(n)=(a_{1}+1) \cdots (a_{k}+1)=\prod\limits_{i=1}^{k}(a_{i}+1) \]Il seguente teorema è stato dimostrato da Carl Gustav Jacobi (1804-1851), uno dei più grandi matematici del secolo XIX. Uno dei suoi maggiori contributi è la teoria delle funzioni ellittiche e delle funzioni theta, sviluppata nella sua importante opera ‘Fundamenta nova theoriae functionum ellipticarum’, pubblicata in latino nel \(1829\).
Teorema 2.4 – Jacobi
\[ r_{2}(n)=4(d_{1}(n) – d_{3}(n)) \]dove \(d_{1}(n),d_{3}(n)\) sono rispettivamente il numero di divisori positivi di \(n\) della forma \(4k+1\) e \(4k+3\).
Il teorema 4.2 è stato inizialmente dimostrato da Jacobi mediante la sua teoria delle funzioni ellittiche e delle funzioni theta.
Una forma sostanzialmente equivalente del teorema era stata dimostrata anche da Gauss nella sua opera fondamentale ‘Disquisitiones Arithmeticae’, pubblicata nel \(1801\) in latino.
Per una dimostrazione vedere articolo su questo sito.
Esercizio 2.2
Mediante la formula di Jacobi dimostrare le seguenti formule:
3) Il problema del cerchio di Gauss
Ricordiamo la definizione di reticolo (vedi anche articolo su questo sito).
Nel piano ogni punto \(P\) è individuato dalle due coordinate cartesiane: \(P=(x,y)\). Un punto può essere rappresentato da un vettore \(\mathbf{OP}\) che va dall’origine al punto stesso. La somma \(S=P+Q\) di due punti \(P,Q\) è rappresentata dal punto corrispondente alla somma vettoriale dei due vettori \(\mathbf{OP}\) e \(\mathbf{OQ}\).
Definizione 3.1
Un insieme \(L\) di punti del piano \(R^{2}\) è un reticolo (lattice) se soddisfa le seguenti condizioni:
- è un gruppo con l’operazione di somma di punti
- ogni punto è il centro di un cerchio privo di altri punti dell’insieme \(L\)
La seconda condizione implica che i punti di un reticolo sono punti isolati.
Sostanzialmente un reticolo è una configurazione infinita di punti disposti con regolarità e con simmetria. Esistono diversi tipi di reticoli utilizzati in vari settori della matematica, della fisica, ecc.
Il più semplice e importante che verrà utilizzato in questo articolo è il reticolo piano formato dalle rette parallele agli assi coordinati a distanza unitaria, in un sistema cartesiano ortogonale. L’insieme dei punti del reticolo viene indicato con il simbolo \(\Lambda\).
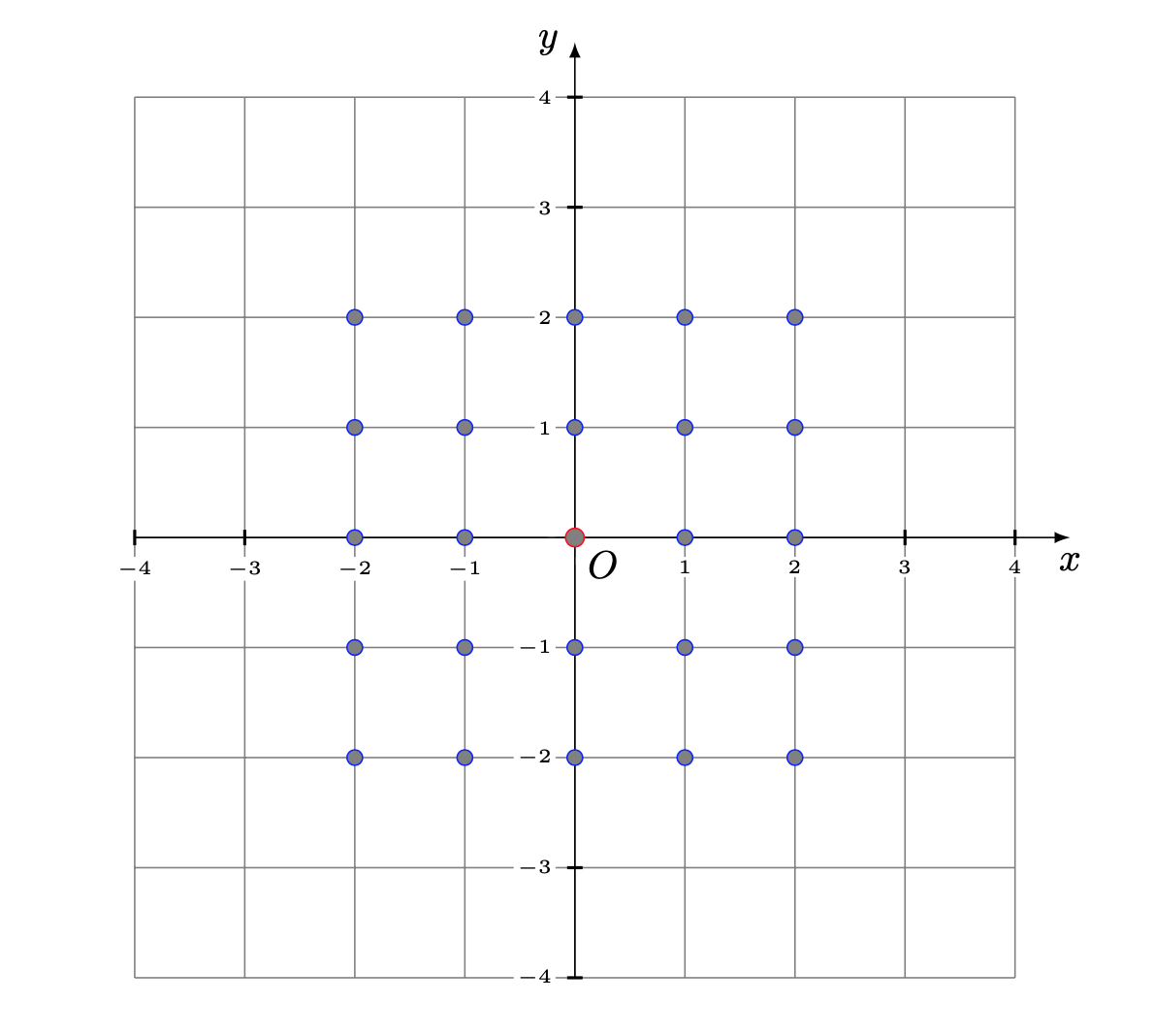
Definiamo ora il problema del cerchio di Gauss.
Sia \(n\) un intero non negativo. Indichiamo con \(N(n)\) il numero dei punti contenuto all’interno e sulla frontiera di un cerchio di raggio \(\sqrt{n}\) con centro nell’origine del reticolo fondamentale \(\Lambda\).
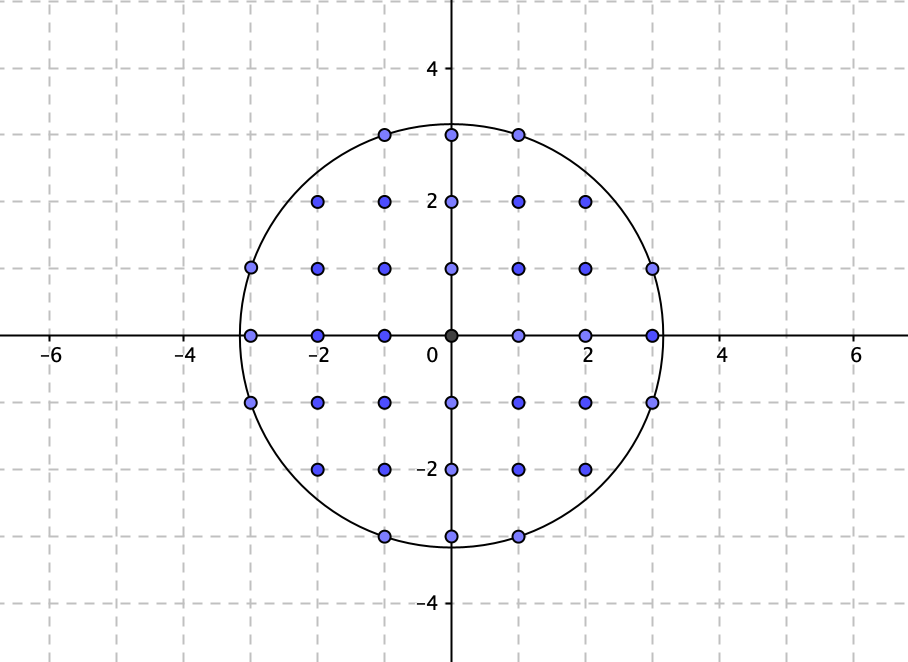
Il problema del cerchio di Gauss consiste nel calcolare il numero \(N(n)\) per un dato intero non negativo \(n\).
Consideriamo ora la seguente somma \(T(n)\):
Poiché \(r_{2}(k)\) è uguale al numero dei punti interi che stanno sul cerchio di equazione \(x^{2}+ y^{2}=k\), allora \(T(n)\) rappresenta il numero delle soluzioni intere della seguente disuguaglianza:
\[ 0 \le x^{2}+ y^{2} \le n \ , \quad x,y \in \mathbb{Z} \]In altri termini \(T(n)\) è uguale al numero dei punt interi del piano contenuti nel cerchio di centro nel punto \((0,0)\) e raggio uguale a \(\sqrt{n}\).
Quindi abbiamo \(N(n) = T(n)\).
Esempio 3.1
Nella seguente tabella sono riportati i numeri dei punti interi all’aumentare del raggio del cerchio.
Come si può notare dalla tabella il rapporto \(\dfrac{N(n)}{n}\) si avvicina al valore di \(\pi\), al crescere del raggio del cerchio. Questo è confermato dal seguente teorema.
Teorema 3.1 – Gauss
\[ \lim_{n \to \infty}\frac{N(n)}{n}= \lim_{n \to \infty}\frac{1}{n} \sum\limits_{k=0}^{n}r_{2}(k)= \pi \]Prima dimostrazione
Diamo solo una traccia della dimostrazione. Consideriamo la seguente figura:
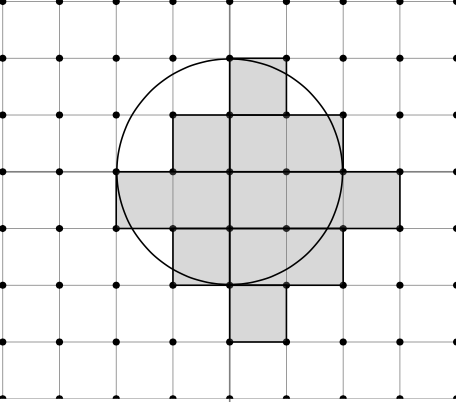
Ad ogni punto \(P\) contenuto nel cerchio associamo un quadrato nel quale il punto \(P\) è il vertice superiore sinistro. Ogni quadrato ha lato uguale ad 1 e diagonale \(\sqrt{2}\). Il numero \(N(n)\) è uguale all’area ombreggiata.
Possiamo approssimare l’area ombreggiata dal basso e dall’alto. L’area ombreggiata è contenuta in un cerchio di raggio \((\sqrt{n}+ \sqrt{2})\) e contiene il cerchio di raggio \((\sqrt{n}- \sqrt{2})\). All’aumentare del raggio del cerchio, il numero dei punti interi dell’area ombreggiata si avvicina all’area del cerchio \(\pi n\). Nei paragrafi successivi vedremo la stima dell’errore di approssimazione.
Seconda dimostrazione
Utilizziamo la formula di Jacobi \(r_{2}(n)=4(d_{1}(n) – d_{3}(n))\). Abbiamo
Utilizzando la formula di Leibniz per il calcolo di \(\pi\)
\[ \frac{\pi}{4} = 1 – \frac{1}{3}+ \frac{1}{5}- \frac{1}{7}+\cdots \]otteniamo subito il risultato.
Esercizio 3.1
Dimostrare che il numero totale dei divisori della forma \(4k+1\) che non superano \(n\) è
Dimostrare che il numero totale dei divisori della forma \(4k+3\) che non superano \(n\) è
\[ \left\lfloor \frac{n}{3}\right\rfloor + \left\lfloor \frac{n}{7}\right\rfloor + \left\lfloor \frac{n}{11}\right\rfloor + \cdots \]Esempio 3.2
Calcolare il numero dei punti interi contenuti in un cerchio di raggio uguale a \(6\).
Esercizio 3.3
Dimostrare che \(T(100)=317\).
Utilizzare la formula seguente:
4) Formula di Sierpinski
Dimostriamo ora la formula di Sierpinski, che permette un calcolo più veloce del valore di \(T(n)=r_{2}(0) + r_{2}(1) + \cdots + r_{2}(n)\).
Teorema 4.1 – Sierpinski
\[ T(n)= 1+ 4 \sum\limits_{k=0}^{[\sqrt{n}]}\left[\sqrt{n-k^{2}}\right] \]Dimostrazione
Il valore di \(T(n)\) è il numero delle soluzioni intere della disuguaglianza
Trattiamo separatamente la soluzione \((x,y)=(0,0)\). Dividiamo le altre soluzioni in classi disgiunte: due soluzioni \((x_{1},y_{1})\) e \((x_{2},y_{2})\) appartengono alla stessa classe se e solo se i valori della coordinata \(x\) sono uguali, cioè se \(x_{1}=x_{2}\). Dobbiamo calcolare il numero di soluzioni in ognuna di queste classi.
Se \(x=0\) il numero delle soluzioni è dato dai valori di \(y\) tali che \(|y| \le \sqrt{n}\), quindi è uguale a \(2 \lfloor \sqrt{n} \rfloor \).
Supponiamo ora \(x= k \neq 0\). Allora \(k^{2} \le n\) e quindi \(|y| \le \sqrt{n-k^{2}}\). Il numero di questi \(y\) è uguale a \( 1+ 2 \lfloor \sqrt{n-k^{2}}\rfloor\). Il numero \(k\) può assumere i valori \(\pm1, \pm2, \cdots, \pm \lfloor \sqrt{n}\rfloor\). Mettendo insieme abbiamo
La formula di Sierpinski permette di calcolare i valori di \(T(n)\) con maggiore efficienza.
Esempio 4.1
Calcoliamo nuovamente \(T(36)\) con la formula di Sierpinski.
Per una esposizione molto chiara ed interessante del problema di Gauss vedere il testo classico di Hilbert[1].
5) Stima dell’errore
5.1) Comportamento asintotico delle funzioni
Nella teoria dei numeri molte funzioni aritmetiche hanno un comportamento irregolare. Ad esempio la funzione \(d(n)\), che conta il numero dei divisori di un intero \(n\), assume il valore \(2\) su tutti i numeri primi; d’altra parte può assumere valori grandi a piacere, ad esempio \(d(2^{k})=k+1\), al tendere di \(k\) all’infinito. La funzione quindi non tende ad un valore definito al crescere di \(n\), ma oscilla indefinitivamente fra il valore minimo e valori grandi a piacere.
In molti casi quindi è impossibile descrivere esattamente il comportamento di una funzione aritmetica \(f(n)\) per grandi valori di \(n\). Spesso è più utile studiare il comportamento della somma parziale
oppure della media aritmetica
\[ S(n)=\frac{1}{n} \sum\limits_{k=1}^{n}f(k) \]Il simbolo di Landau
Sia \(g(n)\) definita sugli interi e a valori reali positivi. La notazione O-grande di E. Landau (1877-1938)
significa che esiste una costante positiva \(K > 0\) tale che
\[ |f(n)| \le K g(n) \ ,\quad n \ge n_{0} \]dove \(n_{0}\) è un numero reale opportuno.
In realtà sarebbe più esatto scrivere \(f(n) \in O(g(n))\), cioè la funzione \(f(n)\) appartiene all’insieme \(O(g(n))\) delle funzioni limitate dalla \(g(n)\).
La notazione di Landau si estende naturalmente anche su funzioni di variabile reale.
Esempio 5.1
Per \(n \to \infty\) verificare le seguenti formule:
5.2) Stima dell’errore di Gauss
In precedenza abbiamo visto che il numero \(N(n)\) dei punti interi all’interno del cerchio di raggio \(\sqrt{n}\) è approssimativamente uguale all’area del cerchio \(\pi n\). Gauss dimostrò il seguente teorema per la stima dell’errore di approssimazione:
Teorema 5.1
\[ T(n)=\sum\limits_{0 \le k \le n}^{}r_{2}(k)=\pi n + O(\sqrt{n}) \]Dimostrazione
Dalla figura precedente (figura 1) possiamo dedurre le seguenti disuguaglianze:
Da queste deriva subito
\[ \begin{array}{l} T(n) = \pi n + O(\sqrt{n}) \end{array} \]5.3) Miglioramenti della stima di Gauss
Nel \(1906\) il matematico polacco Sierpinski ha pubblicato un miglioramento della stima di Gauss. La formula di Sierpinski è la seguente:
\[ \sum\limits_{k=0}^{n}r_{2}(k)=\pi n + O\left(n^{1/3}\right) \]In seguito, utilizzando strumenti matematici molto complessi, sono state ottenute delle stime più precise da parte di diversi matematici. Tra questi ricordiamo van per Corput, Landau, Hardy e Erdos.
Per approfondire vedere il testo classico di Hardy-Wright[2].
6) Estensione del problema del cerchio a dimensioni maggiori
Un prima generalizzazione del problema del cerchio di Gauss è lo studio dei punti \(P=(x,y,z)\) a coordinate intere contenuti in una sfera dello spazio \(\mathbb{R}^{3}\), centrata nell’ordine del sistema di coordinate. Ma si può estendere anche a dimensioni maggiori di \(3\), analizzando i punti interi contenuti in un ipersfera, che è una generalizzazione del cerchio e della sfera ordinaria.
6.1) Cerchio, sfera e ipersfera
Definizione 6.1
Una d-ipersfera \(S_{d}\) di raggio \(R \gt 0\) è l’insieme dei punti \(P=(x_{1},\cdots,x_{d})\) dello spazio euclideo \(\mathbb{R}^{d}\) che soddisfano la seguente relazione:
In questa definizione il valore del parametro \(d\) è uguale al numero delle coordinate dello spazio euclideo nel quale la figura è immersa.
- Nel caso \(d=1\), si tratta di un segmento con centro nell’origine e lunghezza uguale a \(2R\).
- Nel caso \(d=2\), è un cerchio di raggio \(R\).
- Nel caso \(d=3\), è una sfera ordinaria di raggio \(R\), immersa nello spazio euclideo a tre dimensioni.
- Nel caso \(d \gt 3\), è una d-ipersfera di dimensione \(d\) immersa nello spazio euclideo di dimensione \(d\).
Per determinare il volume della d-ipersfera dobbiamo calcolare il seguente integrale multiplo:
\[ \begin{array}{l} V_{d}(R) = \int\limits_{D} dx_{1}dx_{2} \dots dx_{d}=K_{d}R^{d} \end{array} \]dove \(D=\{(x_{1}, \cdots,x_{d}): x_{1}^{2}+ \cdots + x_{d}^{2} \le R^{2}\}\) è la d-ipersfera di raggio \(R\) e il fattore \(K_{d}\) rappresenta il volume della d-ipersfera di raggio unitario.
La superficie della frontiera della d-ipersfera, indicata con \(S_{d-1}(R)\), è correlata al volume dalle seguenti formule:
Ricordiamo la definizione della funzione Gamma, che appare nelle formule per il volume e la superficie della frontiera di una d-ipersfera:
\[ \Gamma(x)= \int\limits_{0}^{\infty}t^{x-1}e^{-t}dt \ ,\quad x \gt 0 \]Esercizio 6.1
Dimostrare la seguente formula:
Vale il seguente teorema:
Teorema 6.1
\[ \begin{array}{l} V_{d}(R) = \dfrac{\pi^{d/2} R^{d}}{\Gamma\left(1+ \frac{d}{2}\right)} \\ S_{d-1}(R)= \dfrac{d\pi^{d/2} R^{d-1}}{\Gamma\left(1+\frac{d}{2}\right)} \end{array} \]Per una dimostrazione vedere ad esempio [3].
Nella seguente tabella riportiamo le formule per il calcolo della superficie della frontiera e del volume della d-ipersfera al variare del parametro \(d\): .
\[ \begin{array}{|c|c|c|c|} \hline \text{Dimensione} & \text{Nome} & \text{Superficie} & \text{Volume} \\ \hline 1 & \text{Segmento} & 2 & 2R \\ \hline 2 & \text{Cerchio} & 2\pi R & \pi R^{2} \\ \hline 3 & \text{Sfera} & 4\pi R^{2} & \dfrac{4 \pi}{3} R^{3} \\ \hline 4 & \text{4-ipersfera} & 2 \pi^{2} R^{3} & \dfrac{\pi^{2}}{2} R^{4} \\ \hline 5 & \text{5-ipersfera} & \frac{8}{3}\pi^{2} R^{4} & \dfrac{8\pi^{2}}{15} R^{5} \\ \hline 6 & \text{6-ipersfera} & \pi^{3} R^{5} & \dfrac{\pi^{3}}{6} R^{6} \\ \hline \end{array} \]Esercizio 6.2
Dimostrare la seguente formula di ricorsione
Esercizio 6.3
Dimostrare che
Esercizio 6.4
Studiare l’andamento della funzione \(f(k)=V_{k}(1)\). Dimostrare che si tratta di una funzione prima crescente, poi raggiunge un massimo per \(d=5\) e quindi decresce.
All’aumentare della dimensione il volume della d-ipersfera di raggio unitario tende a zero.
Per studiare le proprietà della funzione gamma vedere [5].
6.2) Estensione del problema di Gauss
Indichiamo con \(N_{d}(n)\) il numero dei punti interi contenuti in una d-ipersfera con raggio uguale a \(\sqrt{n}\).
Il teorema dimostrato da Gauss si riferisce al caso \(d=2\), cioè al cerchio:
Il significato geometrico è che il numero dei punti interi contenuti nel cerchio di raggio \(\sqrt{n}\) è approssimativamente uguale all’area del cerchio \(A=\pi n\).
Possiamo estendere il problema di Gauss a dimensioni maggiori. Ad esempio nel caso \(d=3\), cioè della sfera, possiamo aspettarci che il numero di punti interi contenuti nella sfera di raggio \(\sqrt{n}\) sia approssimativamente uguale al volume della sfera:
Esistono varie stime dell’errore. Ricordiamo in particolare la stima del matematico russo Vinogradov:
\[ \begin{array}{l} N_{3}(n)= \frac{4}{3}\pi n^{3/2}+ O(n^{19/28 + \epsilon}) \ ,\quad \epsilon \gt 0 \end{array} \]Il problema nel caso generale è naturalmente molto complesso. Per analogia nel caso \(d \gt 3\) si può supporre una formula del seguente tipo:
\[ \begin{array}{l} N_{d}(n)= \dfrac{\pi^{d/2}}{\Gamma\left(1 + \frac{d}{2}\right)} n^{d/2}+ O(n^{\theta/2}) \end{array} \]con il valore \(\theta \) da determinare.
Per approfondire vedere [4].
Conclusione
Il problema del cerchio di Gauss è un classico esempio di problema della teoria dei numeri formulato in termini geometrici. La soluzione di molti problemi della teoria dei numeri dipende dalla capacità di determinare i punti a coordinate intere contenuti in una data regione dello spazio euclideo \(\mathbb{R}^{n}\). Ad esempio, il problema fondamentale ed estremamente complesso di determinare i divisori di un intero positivo \(n\) equivale a trovare i punti a coordinate intere sull’iperbole \(xy=n\).
In articoli successivi vedremo altri esempi interessanti di problemi di teoria dei numeri studiati tramite metodi geometrici.
Bibliografia
[1]Hilbert, Cohn-Vossen – Geometria Intuitiva (Boringhieri)
[2]Hardy, Wright – An Introduction to the Theory of Numbers (Oxford U.P.)
[3]Sommerville – An Introduction to the Geometry of N Dimensions (Dover)
[4]Chamizo, Iwaniec – On the Sphere Problem (Revista Matemática Iberoamericana (1995), Volume: 11, Issue: 2, page 417-429)
[5]Spiegel, Wrede – Schaum’s Outline of Advanced Calculus (McGraw Hill)
0 commenti