Processi Stocastici e Catene di Markov – Teoria e Applicazioni

Le catene di Markov sono un modello stocastico utile per modellizzare e analizzare sistemi che evolvono secondo certe distribuzioni di probabilità. È un processo stocastico importante che ha trovato applicazione in diversi settori: fisica, biologia, scienze sociali, economia, ingegneria, ecc.
La teoria delle catene di Markov è stata inizialmente sviluppata dal matematico russo Andrei Markov (1856-1922), un discepolo del famoso matematico Chebyshev all’Università di San Pietroburgo.
Si tratta di una naturale generalizzazione del modello di prove indipendenti di Bernoulli. Consideriamo una serie di prove di un esperimento, dove il risultato alla prova \(n\)-esima è un evento \(A_{n}\) che assume solo due possibili risultati, ad esempio vero/falso. Le prove si dicono prove di Bernoulli indipendenti se per ogni intero \(n\) risulta

\[ P(A_{n+1}|A_{1},A_{2}, \cdots, A_{n})=P(A_{n+1}) \]

Un esempio classico è il lancio di una moneta, che prevede due risultati, testa e croce. Il risultato alla prova \((n+1)\)-esima non dipende dai risultati delle prove precedenti.
Nel caso delle catene di Markov il risultato della prova \((n+1)\)-esima dipende solo dal risultato della prova immediatamente precedente. Cioè

\[ P(A_{n+1}|A_{1},A_{2}, \cdots, A_{n})=P(A_{n+1}|A_{n}) \]

Si dice in questo caso che le prove non hanno memoria.
In questo articolo introduciamo il concetto importante di processo stocastico e studiamo in particolare le proprietà delle catene di Markov, presentando alcune applicazioni significative.

1) Spazi di probabilità e variabili aleatorie

Ricordiamo brevemente alcuni concetti di calcolo delle probabilità. Un esperimento casuale è un processo che produce dei risultati non prevedibili con certezza. L’insieme di tutti i risultati possibili di un esperimento si chiama spazio campionario o spazio degli eventi. I sottoinsiemi dello spazio campionario si chiamano eventi. Un evento elementare, chiamato anche punto dello spazio campionario, contiene un singolo risultato di un esperimento.
Ricordiamo la definizione assiomatica di Kolmogorov per costruire la teoria della probabilità (per maggiori dettagli vedere vedi l’articolo su questo sito). Il modello matematico di Kolmogorov si basa su una terna di elementi \((\Omega,\mathfrak{F},P)\), chiamata spazio di probabilità:

\[ \begin{array}{l} 1) \quad \Omega: \quad \text{ spazio degli eventi elementari}\\ 2) \quad \mathfrak{F}: \quad \sigma \text{-algebra di eventi} \\ 3) \quad P: \mathfrak{F} \to [0,1] \quad \text{funzione di probabilità} \end{array} \]

L’insieme \(\Omega\) è lo spazio degli eventi elementari e rappresenta l’insieme di tutti i possibili risultati dell’esperimento. La \(\sigma\)-algebra \(\mathfrak{F}\) contiene gli eventi collegati all’esperimento. La funzione probabilità \(P: \mathfrak{F} \to [0,1]\) è definita sugli eventi casuali e soddisfa i seguenti assiomi:

\[ \begin{array}{l} 1) \quad P(\Omega)=1 \\ 2) \quad P(\emptyset)=0 \\ 3) \quad P\left(\bigcup_{k} A_{k}\right)=\sum_{k}P(A_{k}) \end{array} \]

dove nel terzo assioma gli eventi \(A_{k}\) sono incompatibili a coppie.

Esempio 1.1
Supponiamo di effettuare il lancio di una moneta. Allora abbiamo

\[ \Omega=\{T,C\} \ ,\quad \text{T =testa} \ ,\quad \text{C=croce} \]

La \(\sigma\)-algebra corrispondente è

\[ \mathfrak{F}=\{\emptyset, \Omega, \{T\}, \{C\}\} \]

Notiamo che la funzione probabilità di Kolmogorov è definita solo per gli eventi della \(\sigma\)-algebra, mentre non è definita per gli eventuali sottoinsiemi di \(\Omega\) non appartamenti alla \(\sigma\)-algebra.
Il modello assiomatico di Kolmogorov è basato sulla teoria della misura, una branca della matematica che ha un ruolo fondamentale in molti settori, tra cui il calcolo integrale, la teoria della probabilità, l’analisi funzionale, la teoria dei sistemi dinamici.

Probabilità condizionata
La probabilità sopra definita viene anche chiamata probabilità incondizionata, in quanto non viene imposto alcun vincolo aggiuntivo, oltre i vincoli di coerenza espressi dagli assiomi di Kolmogorov. In altre situazioni la determinazione della probabilità degli eventi può dipendere da condizioni supplementari.
Ad esempio calcolare la probabilità di un evento \(A\), dato che è noto che si è verificato un evento \(B\), in qualche modo collegato con l’evento \(A\). In questi casi la probabilità cercata viene indicata con il simbolo \(P(A|B)\) e viene chiamata probabilità condizionata. Questa è legata alla probabilità incondizionata dalla seguente relazione:

\[ \begin{array}{l} P(A|B)= \dfrac{P(A \cap B)}{P(B)} \end{array} \]

Il concetto base è che la valutazione della probabilità di un evento dipende in modo essenziale dallo stato di informazione del soggetto. Il calcolo della probabilità condizionata viene effettuato riducendo lo spazio campionario e calcolando la probabilità in questo spazio ridotto. Naturalmente se \(P(B)=0\) allora la formula perde di significato.

Esercizio 1.1
Dimostrare che la funzione \(P(A|B)\) soddisfa gli assiomi di Kolmogorov.

Esercizio 1.2
Vengono lanciati due dadi. Calcolare la probabilità che la somma dei due numeri sia uguale a \(8\), sapendo che la somma è un numero pari.
Soluzione: \(\left[p=\dfrac{5}{18}\right]\)

Esercizio 1.3
Vengono estratte due carte da un mazzo di carte da poker, di \(52\) carte. Calcolare la probabilità che la seconda carta sia un Re, dato che la prima è un Re.
Soluzione: \(\left[p=\dfrac{3}{51}\right]\)

1.1) Variabili aleatorie

Una variabile aleatoria \(X\) è una funzione che assegna un numero reale ad ogni evento possibile di uno spazio campionario. In simboli:

\[ X: \omega \to X(\omega) \in \mathbb{R} \ ,\quad \omega \in \Omega \]

In termini matematici più precisi una variabile aleatoria è una funzione a valori reali \(X\) misurabile, definita sullo spazio campionario \(\Omega\):

\[ X: \Omega \to \mathbb{R} \]

Il concetto di funzione misurabile significa che per ogni numero reale \(x\) l’insieme

\[ E_{x}=\{\omega \in \Omega: X(\omega) \lt x\} \]

appartiene alla \(\sigma\)-algebra \(\mathfrak{F}\).
Una variabile aleatoria si dice discreta se assume solo un numero finito di valori, oppure una infinità numerabile (ad esempio i numeri naturali o i numeri interi). In caso contrario si dice continua.
Una variabile aleatoria discreta è rappresentata dalla sua distribuzione di probabilità, cioè dalla lista delle probabilità assegnate a tutti i possibili valori. Data una variabile aleatoria \(X\) che assume i valori \(\{x_{k}, \ k=1,2,\cdots\} \), indichiamo con \(p_{k}=P(X=x_{k})\) la probabilità che la variabile aleatoria assuma il valore \(x_{k}\). Chiaramente si ha:

\[ \begin{array}{l} \sum\limits_{k=1}^{\infty}p_{k}= 1 \ ,\quad p_{k} \ge 0 \end{array} \]

La somma naturalmente può essere finita. La distribuzione di probabilità si chiama anche funzione di massa di probabilità.
La funzione di ripartizione \(F(x)\) di una variabile aleatoria \(X\) è così definita:

\[ F(x) = P(X \le x) \]

Chiaramente si ha \(F(-\infty)=0\) e \(F(+\infty)=1\).

Media e varianza di una variabile aleatoria
Due parametri importanti che descrivono le proprietà di una variabile aleatoria discreta \(X\) sono la media \(E(X)\) e la varianza \(Var(X)\):

\[ \begin{array}{l} \mu=E(X)=\sum\limits_{k}^{}x_{k}P(X=x_{k})=\sum\limits_{k}^{}x_{k}p_{k} \\ \sigma^{2}= Var(X)=E[(X-\mu)^{2}]= E(X^{2}) – \mu^{2} \end{array} \]

Nel caso continuo non si calcola la probabilità che la variabile assuma un valore preciso in un punto, ma si calcola la probabilità che la variabile aleatoria assuma valori in un dato intervallo reale \([a,b]\). Per questo viene definita la funzione densità di probabilità \(f(x)\), associata alla variabile aleatoria \(X\), nel seguente modo:

\[ P(a \le X \le b)= \int\limits_{a}^{b}f(x)dx \]

La funzione densità di probabilità soddisfa la seguente relazione:

\[ \begin{array}{l} \int\limits_{-\infty}^{\infty}f(x)dx=1 \ ,\quad f(x) \ge 0 \end{array} \]

La funzione di distribuzione di una variabile aleatoria continua è

\[ F(x) =P(X \le x)= \int\limits_{-\infty}^{x}f(t)dt \]

È facile verificare che se la funzione \(f(x)\) è continua allora

\[ \frac{dF(x)}{dx}= f(x) \]

La media e la varianza di una variabile aleatoria continua sono così definite:

\[ \begin{array}{l} \mu=E(X)=\int\limits_{-\infty}^{+\infty}x f(x)dx \\ \sigma^{2}=Var(X)=E[(X-\mu)^{2}]= \int\limits_{-\infty}^{+\infty}x^{2} f(x)dx – \mu^{2}\\ \end{array} \]

Esercizio 1.4
Dimostrare le seguenti relazioni:

\[ \begin{array}{l} 0 \le F(x) \le 1 \\ F(a) \le F(b) \quad \text{se } a \lt b \\ \lim\limits_{x \to -\infty}F(x) = 0 \\ \lim\limits_{x \to +\infty}F(x) = 1 \\ \end{array} \]

Esercizio 1.5
Sia \(a\) un numero reale. Dimostrare le seguenti relazioni:

\[ \begin{array}{l} E(a) = a \\ E(aX) = a E(X) \\ E(X + Y) = E(X) + E(Y) \\ Var(a) = 0 \\ Var(aX) = a^{2}Var(X) \\ Var (a+ X) = Var(X) \end{array} \]

Esempio 1.2 – Distribuzione di Bernoulli
Una variabile aleatoria di Bernoulli \(X\) assume due soli valori, ad esempio \(\{0,1\}\), con probabilità

\[ \begin{array}{l} P(X=1)=p \\ P(X=0)=q=1-p \end{array} \]

Chiaramente \(E(X)=p\) e \(Var(X)=pq\).

Esercizio 1.6 – Distribuzione geometrica
Supponiamo di effettuare prove ripetute indipendenti di Bernoulli. Vogliamo calcolare il numero di prove necessarie per avere il primo successo. Indichiamo con \(X\) la variabile aleatoria che conta il numero di fallimenti prima di avere un successo. I valori possibili sono \(X=\{0,1,2,\cdots\}\). La distribuzione di probabilità di \(X\) è la distribuzione geometrica:

\[ P(X=k)= (1-p)^{k}p \ ,\quad k=0,1,2,\cdots \]

Dimostrare che \(E(x)=\dfrac{q}{p}\) e \(Var(X)= \dfrac{q}{p^{2}}\).

Esercizio 1.7
Estendere l’esempio precedente calcolando il numero di prove da fare fino ad ottenere \(r\) successi. Indichiamo con \(X\) la variabile aleatoria che conta il numero di fallimenti osservati prima di avere \(r\) successi. I valori possibili sono \(X=\{0,1,2,\cdots\}\). Dimostrare che la distribuzione di probabilità di \(X\) è la seguente

\[ P(X=k)=\binom{k+r-1}{r-1}p^{r}(1-p)^{k} \ ,\quad k=0,1,2,\cdots \]

Questa si chiama distribuzione di Pascal, o anche distribuzione binomiale negativa.

Esercizio 1.8 – Distribuzione Poisson
La distribuzione di Poisson con parametro \(\lambda \gt 0\) è la seguente:

\[ P(X=k)= e^{-\lambda}\frac{\lambda^{k}}{k!} \ ,\quad k=0,1,2,\cdots \]

Dimostrare che \(E(X)=\lambda\) e \(Var(X)= \lambda\).

Esercizio 1.9 – Distribuzione esponenziale
La distribuzione esponenziale con parametro \(\lambda \gt 0\) ha la seguente densità di probabilità:

\[ f(x) = \begin{cases} \lambda e^{-\lambda x} \ ,\quad x \ge 0 \\ 0 \ ,\quad x \lt 0 \end{cases} \]

Dimostrare che

\[ \begin{array}{l} \mu=E(X)=\dfrac{1}{\lambda} \\ Var(X)=\sigma^{2} = \dfrac{1}{\lambda^{2}} \\ P(X \gt t) = e^{-\lambda t} \ ,\quad t \ge 0 \end{array} \]

Esercizio 1.10 – Distribuzione normale
La distribuzione normale con parametri \(\mu\) e \(\sigma^{2}\), indicata con \(N(\mu,\sigma^{2})\), ha la seguente densità di probabilità:

\[ f(x)= \frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\dfrac{(x -\mu)^{2}}{2\sigma^{2}}} \ ,\quad -\infty \lt x \lt \infty \]

Dimostrare che \(E(X)= \mu\) \(Var(X)= \sigma^{2}\).
Dimostrare inoltre che il massimo si ha nel punto \(x=\mu\).
Nel caso \(\mu=0\) e \(\sigma=1\), la \(N(0,1)\) viene chiamata distribuzione normale standard.

1.2) Distribuzioni congiunte di variabili aleatorie

Ricordiamo il concetto di distribuzione congiunta di variabili aleatorie. Per semplicità ci limitiamo al caso di due variabili aleatorie, ma le definizioni si estendono in modo naturale al caso di \(n \gt 2\) variabili aleatorie.
Due variabili aleatorie \(X,Y\) si dicono congiuntamente distribuite se sono definite nello stesso spazio di probabilità. In questo caso si possono fare valutazioni probabilistiche sui valori assunti simultaneamente dalle due variabili aleatorie.

1.2.1) Variabili aleatorie discrete

Siano \(X,Y\) due variabili aleatorie discrete. La funzione di probabilità congiunta di \(X\) e \(Y\) è così definita:

\[ p_{X,Y}(x,y)=P(X=x,Y=y) \]

dove

\[ \begin{array}{l} \sum\limits_{x,y}{}p_{X,Y}(x,y)=1 \ ,\quad p_{X,Y}(x,y) \ge 0 \end{array} \]

La funzione di distribuzione congiunta di \(X,Y\) è definita

\[ \begin{array}{l} F(x,y)= P(X \le x, Y \le y)=\sum\limits_{u \le x}{}\sum\limits_{v \le y}{}p_{X,Y}(u,v) \end{array} \]

Dalla distribuzione congiunta possiamo ricavare le funzioni di probabilità marginali delle singole variabili aleatorie:

\[ \begin{array}{l} p_{X}(x)= \sum\limits_{y}{}p_{X,Y}(x,y) \\ p_{Y}(y)= \sum\limits_{x}{}p_{X,Y}(x,y) \\ \end{array} \]

In modo simile, dalla conoscenza della funzione di distribuzione congiunta possiamo ricavare le funzioni di distribuzioni di probabilità delle singole variabili aleatorie, chiamate funzioni di distribuzione marginali:

\[ \begin{array}{l} F_{X}(x)=P(X \le x)=P(X \le x, Y \lt \infty)=F_{X,Y}(x,\infty) \\ F_{Y}(y)=P(Y \le y)=P(X \lt \infty, Y \le y)=F_{X,Y}(\infty,y)\\ \end{array} \]

La funzione di probabilità congiunta di due variabili aleatorie può essere rappresentata mediante le seguente tabella:

\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{X \ Y} & y_{1} & y_{2} & \cdots & y_{m} & \text{Totali} \\ \hline \hline x_{1} & p_{X,Y}(x_{1},y_{1}) & p_{X,Y}(x_{1},y_{2}) & \cdots & p_{X,Y}(x_{1},y_{m}) & p_{X}(x_{1}) \\ \hline x_{2} & p_{X,Y}(x_{2},y_{1}) & p_{X,Y}(x_{2},y_{2}) & \cdots & p_{X,Y}(x_{2},y_{m}) & p_{X}(x_{2}) \\ \hline \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \hline x_{n} & p_{X,Y}(x_{n},y_{1}) & p_{X,Y}(x_{n},y_{2}) & \cdots & p_{X,Y}(x_{n},y_{m}) & p_{X}(x_{n}) \\ \hline \text{Totali} & p_{Y}(y_{1}) & p_{Y}(y_{2}) & \cdots & p_{Y}(y_{m}) & 1 \\ \hline \end{array} \]

1.2.2) Variabili aleatorie continue

Nel caso continuo la funzione di distribuzione congiunta è definita mediante la seguente formula:

\[ \begin{array}{l} F_{X,Y}(x,y)= P(X \le x, Y \le y) \ ,\quad \forall x,y \in \mathbb{R} \end{array} \]

La funzione densità di probabilità congiunta \(f_{X,Y}(x,y)\) permette di calcolare la probabilità che \(a \le X \le b\) e \(c \le Y \le d\), cioè:

\[ \begin{array}{l} P(a \le X \le b, c \le Y \le d)= \int\limits_{x=a}^{b}\int\limits_{y=c}^{d}f_{X,Y}(x,y)dx dy \end{array} \]

Ovviamente si ha

\[ \begin{array}{l} \int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}f_{X,Y}(x,y)dxdy=1 \quad \text{con }f_{X,Y}(x,y) \ge 0 \end{array} \]

Esercizio 1.11
Dimostrare che sotto opportune condizioni vale la seguente formula:

\[ \begin{array}{l} f(x,y) = \dfrac {\partial^{2} F}{\partial x \partial y} \end{array} \]

Esercizio 1.12
Determinare le espressioni delle densità marginali \(f_{X}(x), f_{Y}(y)\) a partire dalla funzione densità congiunta \(f_{X,Y}(x,y)\).

Valore atteso, varianza e covarianza
Sia \(g(x,y)\) una funzione reale di variabili reali. Siano date due variabili aleatorie discrete \(X,Y\), con densità congiunta \(p_{X,Y}(x,y)\). Allora \(g(X,Y)\) è una variabile aleatoria, il cui valore atteso è così definito:

\[ \begin{array}{l} E(g(X,Y)) = \sum\limits_{x} \sum\limits_{y}g(x,y)p_{X,Y}(x,y) \\ \end{array} \]

Nel caso continuo abbiamo

\[ \begin{array}{l} E(g(X,Y))= \int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}g(x,y)f_{X,Y}(x,y)dxdy \\ \end{array} \]

Un esempio importante è \(g(x,y)= x+y\) e quindi \(g(X,Y)=X+Y\). cioè la somma di due variabili aleatorie.

Esercizio 1.13 – Proprietà di linearità della media
Dimostrare la seguente formula:

\[ \begin{array}{l} E(X + Y) = E(X) + E(Y) \\ \end{array} \]

Esercizio 1.14

\[ \begin{array}{l} E(X) = \sum\limits_{x,y}{}xp_{X,Y}(x,y) \\ E(Y) = \sum\limits_{x,y}{}yp_{X,Y}(x,y) \\ \end{array} \]

Covarianza
Siano \(X,Y\) due variabili aleatorie con varianza finita. La covarianza di \(X,Y\) è

\[ Cov(X,Y)= E\{(X-E(X))(Y-E(Y))\} \]

In particolare \(Cov(X,X) =Var(X)= \sigma^{2}(X)\)

Esercizio 1.15
Dimostrare la seguente espressione della covarianza:

\[ Cov(X,Y)= E(XY) – E(X)E(Y) \]

Esercizio 1.16
Dimostrare la seguente formula

\[ Var(X+Y)= Var(X) + Var(Y) + 2 Cov(X,Y) \]

Variabili aleatorie indipendenti
Il concento di indipendenza di due variabili aleatorie può essere formulato in diversi modi, tra loro equivalenti. Ad esempio sono indipendenti se la funzione di distribuzione congiunta è uguale al prodotto delle singole distribuzioni:

\[ F_{X,Y}(x,y)= F_{X}(x)F_{Y}(y) \quad \forall x,y \]

Oppure, in modo equivalente, se la proprietà vale per la funzione di densità congiunta:

\[ f_{X,Y}(x,y)= f_{X}(x)f_{Y}(y) \quad \forall x,y \]

Regole simili nel caso di variabili aleatorie discrete.
Vale il seguente teorema:

Teorema 1.1
Se due variabili aleatorie \(X,Y\) sono indipendenti allora la covarianza è nulla. In simboli

\[ X,Y \text{ indipendenti} \implies Cov(X,Y)=0 \]

In generale non vale il viceversa, cioè la covarianza può essere nulla anche se le variabili aleatorie non sono indipendenti.

Coefficiente di correlazione
Due variabili aleatorie \(X,Y\) si dicono non correlate se \(Cov(X,Y)=0\), cioè se

\[ E(XY)=E(X)E(Y) \]

La misura della correlazione fra due variabili aleatorie \(X,Y\) è data dal coefficiente di correlazione \(\rho(X,Y)\):

\[ \rho(X,Y)= \frac{Cov (X,Y)}{\sigma(X)\sigma(Y)} \]

Si può dimostrare che

\[ -1 \le \rho(X,Y) \le 1 \]

Esercizio 1.17
Sia data la seguente funzione densità di probabilità congiunta:

\[ f(x,y)= \frac{1}{2} \sin (x+y) \quad 0 \le x,y \le \frac{\pi}{2} \]

Determinare la funzione di distribuzione congiunta, i valori medi \(E(X)\), \(E(Y)\), le varianze e la covarianza.

Soluzione

\[ \begin{array}{l} E(X)=E(Y)=\dfrac{\pi}{4} \\ Var(X)=Var(Y)=\dfrac{\pi^{2}}{16}+ \dfrac{\pi}{2}-2 \\ Cov(X,Y)=\dfrac{\pi}{2}-\dfrac{\pi^{2}}{16}-1 \end{array} \]

Per approfondire la teoria della probabilità vedere ^[1].

2) Processi stocastici

Definizione 2.1
Un processo stocastico con spazio degli stati \(S\) è una collezione di variabili aleatorie \(\{X_{t}: t \in T\}\), definite su uno stesso spazio di probabilità \((\Omega,\mathfrak{F},P)\), che assumono valori in \(S\). Il simbolo \(t\) rappresenta un indice o parametro che può variare in un insieme \(T\), chiamato l’insieme dei parametri o insieme indice.
Lo spazio degli stati è quindi l’insieme dei valori assunti dalle variabili aleatorie \(X_{t}\) al variare del parametro \(t\).
Sia lo spazio dei parametri sia lo spazio degli stati possono essere discreti o continui. Quindi possiamo distinguere \(4\) tipi di processi stocastici:

\[ \begin{array}{|c|c|} \hline \text{Spazio dei Parametri } & \text{Spazio degli Stati } \\ \hline \text{Discreto } & \text{Discreto} \\ \hline \text{Discreto } & \text{Continuo} \\ \hline \text{Continuo} & \text{Discreto} \\ \hline \text{Continuo} & \text{Continuo} \\ \hline \end{array} \]

Esempio 2.1
Come primo esempio, indichiamo con \(X_{n}\) il totale dei punti ottenuti lanciando \(n\) volte un dado. In questo caso \(\{X_{n}\}\) è un processo stocastico discreto, con spazio degli stati \(S=\{1,2,3,4,5,6,7,\cdots\}\) e spazio dei parametri \(T=\{1,2,3,\cdots\}\).

Esempio 2.2
Un processo stocastico tipico della teoria delle code è rappresentato dal numero di arrivi o partenze in un dato intervallo di tempo.
Ad esempio il numero di persone in attesa di un autobus in un certo momento del giorno. In questo caso lo spazio dei parametri è continuo e lo spazio degli stati è discreto, in quanto il numero di persone in attesa è un numero intero.

Esempio 2.3
Consideriamo il valore dell’indice azionario in una borsa, alla fine di ogni settimana. Lo spazio dei parametri è discreto e lo spazio degli stati è continuo.

Esempio 2.4 – Il moto browniano
Come esempio di processo stocastico continuo sia nei parametri sia negli stati abbiamo il moto browniano.
Il nome moto Browniano deriva da Robert Brown (1773-1858) che nel 1827 mediante il microscopio osservò il movimento continuo e casuale delle particelle di polline in sospensione nell’acqua.
Il modello del moto browniano, inizialmente nato per descrivere l’evoluzione temporale di fenomeni fisici, in seguito ha trovato applicazione in molti altri settori della matematica e della scienza.

La classificazione dei processi stocastici può essere semplificata considerando solo lo spazio dei parametri, indipendentemente dal fatto che lo spazio degli stati sia numerabile o continuo. Abbiamo allora due categorie fondamentali:

• processi stocastici discreti, se \(T\) è un insieme di valori finito o numerabile;
• processi stocastici continui, se l’insieme dei valori assunti dall’indice dei parametri è un insieme continuo, non numerabile. Ad esempio l’insieme dei numeri reali compresi in in intervallo.

In generale per indicare un processo stocastico si usa la notazione

\[ \{X_{t}: t \in T\} \]

I processi stocastici sono dei modelli per descrivere tutti i possibili risultati di un esperimento casuale. In un esperimento casuale ogni evento elementare \(\omega \in \Omega \) ha una data probabilità di verificarsi. Quindi ad ogni fissato valore di \(t\) corrisponde una variale aleatoria \(X_{t}\):

\[ \begin{array}{l} X_{t}:\Omega \to \mathbb{R} \\ \omega \to X_{t}(\omega) \end{array} \]

Può essere utile immaginare \(t\) come il tempo, e in tal caso \(X_{t}\) rappresenta lo stato al tempo \(t\). Ad esempio nel settore finanziario \(X_{t}\) può rappresentare il valore di un’azione in un determinato giorno dell’anno. In altre situazioni il parametro può rappresentare un punto dello spazio, ad esempio la velocità di una particella in un punto \(t=(x,y,z)\) dello spazio tridimensionale \(\mathbb{R}^{3}\).

Media e varianza di un processo stocastico
Il valore atteso di un processo stocastico \(X_{t}\) è la funzione \(\mu: t \to \mathbb{R}\) seguente:

\[ \mu(t): t \to E(X_{t}) \]

La varianza di un processo stocastico \(X_{t}\) è la funzione \(\sigma^{2}: t \to \mathbb{R}\) seguente:

\[ \sigma^{2}(t): t \to \text{Var}(X_{t}) \]

Traiettorie di un processo stocastico
Un processo stocastico \(\{X_{t}: t \in T\}\) è quindi una funzione di due argomenti:

\[ X: T \times \Omega \to \mathbb{R} \]

Se fissiamo un valore di \(t\), allora abbiamo una variabile aleatoria \(X_{t}\).
Se invece fissiamo un evento \(\omega \in \Omega\), allora la funzione \(t \to X_{t}(\omega)\), definita sull’insieme dei parametri e a valori reali, viene chiamata una realizzazione del processo stocastico. Si usano anche i termini traiettoria o cammino. In genere un processo stocastico genera un numero finito o infinito di traiettorie diverse.
È bene chiarire che con il termine fissare un evento \(\omega\) si intende specificare una successione completa di valori, che determina la traiettoria. Di fatto si fissa un valore \(\omega \in \Omega\) per ogni valore di \(t\).
In termini equivalenti un processo stocastico può anche essere pensato come una funzione casuale del tempo \(t\). Una funzione ordinaria \(F(t)\) assume un valore univoco in corrispondenza di ogni valore della variabile indipendente \(t\). In un processo stocastico \(X_{t}\) invece il valore assunto in corrispondenza di un dato \(t\) è uguale ad una delle diverse realizzazioni dell’esperimento casuale.

Esempio 2.5
È utile analizzare un processo stocastico da entrambi i due punti di vista. Ad esempio possiamo considerare \(X_{n}\) come il valore azionario di una società, e fare previsioni sulla distribuzione di probabilità di \(X_{n}\) in un dato giorno futuro, calcolando la media e la varianza. Dall’altro punto di vista possiamo studiare una realizzazione del processo stocastico, analizzando una successione di valori \(\{x_{1},x_{2}, \cdots,x_{n},\cdots\}\) accaduti, cioè una serie storica del processo.

Esempio 2.6
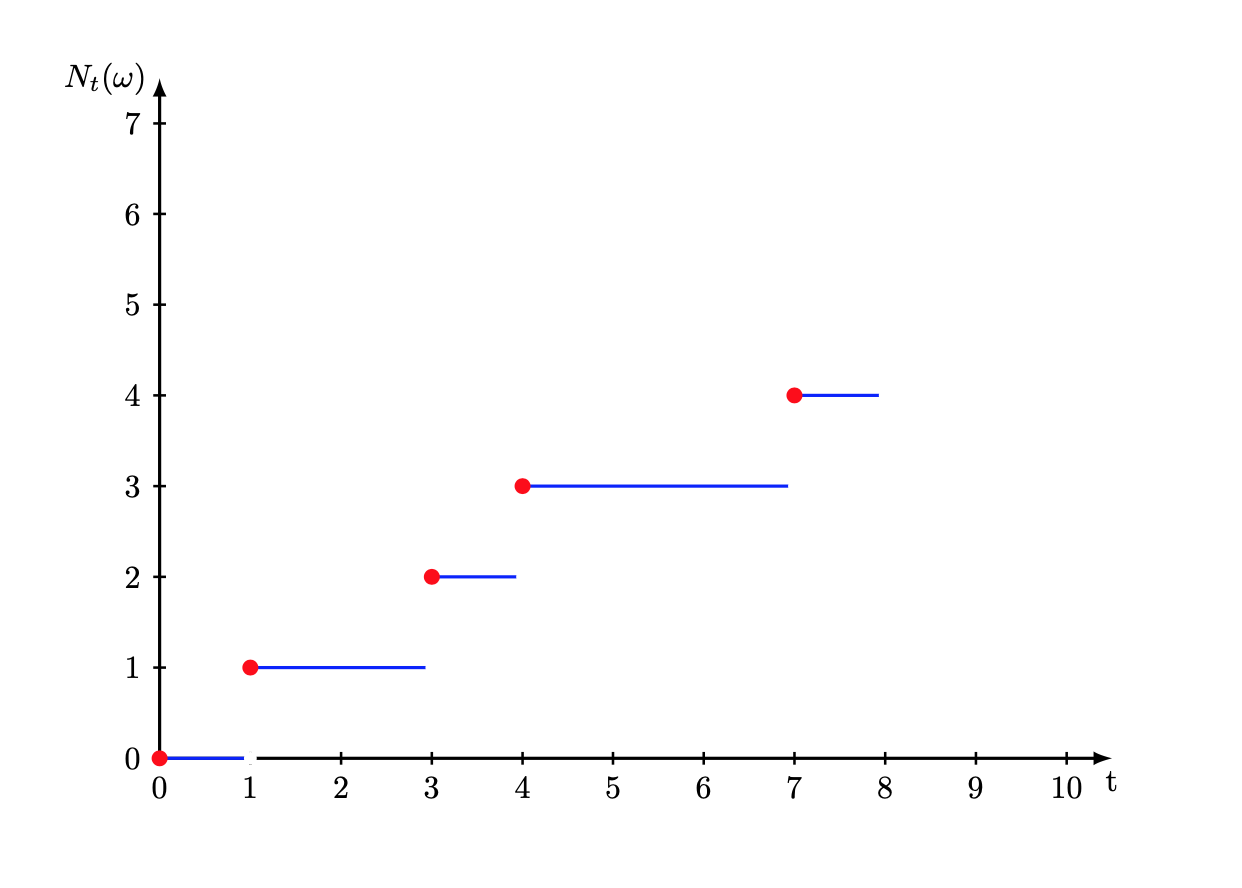
Consideriamo il numero di clienti che arrivano in un supermercato. L’arrivo dei clienti è in genere un processo stocastico, caratterizzato da una distribuzione di probabilità dei tempi di interarrivo \(\omega_{k}\), ovvero gli intervalli di tempo tra gli arrivi di due clienti successivi.
Lo spazio degli eventi è rappresentato da tutte le successioni

\[ \omega = \{w_{1},w_{2},w_{3},\cdots \} \]

Indichiamo con \(N_{t}(\omega)\) il numero di arrivi nell’intervallo \((0,t]\). Chiaramente si ha \(N_{t}(\omega)=k\) se e solo se \(k\) è un intero tale che

\[ w_{1}+w_{2}+ \cdots + w_{k} \le t \lt w_{1}+w_{2}+ \cdots + w_{k+1} \]

Per ogni fissato \(t\), \(N_{t}(\omega)\) è una variabile aleatoria discreta con valori nell’insieme \(S=\{0,1,2,\cdots\}\). Se invece fissiamo \(\omega\), allora la funzione è non decrescente e continua a destra.

Caratterizzazione di un processo stocastico
Consideriamo un insieme finito arbitrario di parametri \(T_{n}=\{t_{1}, \cdots,t_{n}\}\). Allora l’insieme \(\{X_{t_{1}}, \cdots,X_{t_{n}}\}\) è una collezione di variabili aleatorie, caratterizzate dalla loro distribuzione congiunta. La distribuzione congiunta di questa collezione è

\[ F_{T_{n}}= F_{t_{1},\cdots,t_{n}}(x_{1},\cdots,x_{n}) \]

L’insieme di tutte le distribuzioni congiunte \(F_{T_{n}}\) per tutte le possibili partizioni \(T_{n}\) dello spazio dei parametri si chiama distribuzione di dimensione finita del processo stocastico \(\{X_{t}: t \in T\}\).
Kolmogorov ha dimostrato un importante teorema, il quale afferma che la distribuzione di dimensione finita per ogni possibile partizione è sufficiente per caratterizzare un processo stocastico. Più precisamente è possibile definire uno spazio di probabilità \((\Omega,\mathfrak{F},P)\) per il processo stocastico.

2.1) Il processo stocastico di Bernoulli

Consideriamo una successione di variabili aleatorie di Bernoulli \((X_{n}: n=1,2,3,\cdots)\), che assumono solo i due valori \((0,1)\).
Un processo stocastico \(\{X_{n}: n = 1,2, \cdots \}\) viene chiamato processo di Bernoulli con probabilità di successo \(p\) se:

\[ \begin{array}{l} X_{1},X_{2}, \cdots \quad \text{sono indipendenti} \\ P(X_{n}=1) = p \\ P(X_{n}=0)=q=1-p \end{array} \]

Esercizio 2.1
Sia \(\{X_{n}: n \ge 1\}\) un processo di Bernoulli. Dimostrare le seguenti formule:

\[ \begin{array}{l} E(X_{n})=E(X_{n}^{2})= E(X_{n}^{3})= \cdots = p \\ Var (X_{n})= pq \ ,\quad n=1,2,\cdots \end{array} \]

Numero di successi in un processo di Bernoulli
Sia \(\{X_{n}: n \ge 1\}\) un processo di Bernoulli. Per ognuna delle prove indipendenti definiamo successo se \(X_{k}=1\) e fallimento se \(X_{k}=0\):

\[ X_{k} = \begin{cases} 1 \quad \text{successo} \\ 0 \quad \text{fallimento} \end{cases} \]

Consideriamo ora la variabile aleatoria \(N_{n}\), così definita:

\[ \begin{array}{l} N_{n}(\omega) = \begin{cases} 0 \quad \text{se } n=0 \\ X_{1}(\omega)+X_{2}(\omega) + \cdots + X_{n}(\omega) \quad \text{se } n = 1,2,3 \cdots \end{cases} \end{array} \]

dove \(\omega \in \Omega\). Chiaramente \(N_{n}\) rappresenta il numero dei successi alla prova ennesima.

Esercizio 2.2 – Media e varianza del numero dei successi

\[ \begin{array}{l} \mu(N_{n})=E(N_{n})=np \\ Var (N_{n})=\sum\limits_{k=1}^{ n}Var (X_{k})=npq \end{array} \]

Esercizio 2.3

\[ \begin{array}{l} E(N_{n}^{2})=n^{2}p^{2}+ npq \end{array} \]

Esercizio 2.4
Dimostrare che la probabilità di \(k\) successi su \(n\) prove è data dalla distribuzione binomiale di Bernoulli:

\[ P(N_{n}=k)= \binom{n}{k}p^{k}q^{n-k} \ ,\quad k=0,1,\cdots,n \]

Esercizio 2.5
Definiamo \(P_{n}(k)=P(N_{n}=k)\). Dimostrare la seguente relazione ricorsiva:

\[ P_{n+1}(k)=pP_{n}(k-1)+ qP_{n}(k) \]

Esercizio 2.6
Dimostrare che per ogni \(n,r \in \mathbb{N}\) si ha:

\[ P(N_{r+n}-N_{r}=k)= P(N_{n}=k) \ ,\quad k=0,1,\cdots,n \]

Tempo dell’n-esimo successo nel processo di Bernoulli
Sia \(\{X_{n}: n \ge 1\}\) un processo stocastico di Bernoulli con probabilità di successo uguale a \(p\). Consideriamo una realizzazione del processo

\[ \{X_{1}(\omega), X_{2}(\omega), \cdots, X_{n}(\omega), \cdots \}, \quad \omega \in \Omega \]

Abbiamo \(X_{n}(\omega)= 1\) oppure \(X_{n}(\omega)= 0\) per ogni \(n\). Vogliamo studiare i tempi di realizzazione dei successi nelle prove. Indichiamo con \(T_{n}(\omega)\) il tempo di realizzazione dell’ennesimo successo. Ad esempio

\[ \begin{array}{l} X_{1}(\omega)=0, X_{2}(\omega)=1, X_{3}(\omega)=0, X_{4}(\omega)=1, X_{5}(\omega)=1, \cdots \\ T_{1}(\omega)=2, T_{2}(\omega)=4, T_{3}(\omega)=5, \cdots \end{array} \]

Quindi \(T_{n}\) è il numero della prova nella quale si verifica l’ennesimo successo.

Esercizio 2.7
Dimostrare le seguenti relazioni:

\[ \begin{array}{l} T_{k}(\omega) \le n \implies N_{n}(\omega) \ge k \\ N_{n}(\omega) \ge k \implies T_{k}(\omega) \le n \\ T_{k}(\omega) = n \iff N_{n-1}(\omega)=k-1 \land X_{n}(\omega)=1 \end{array} \]

Esercizio 2.8
Dimostrare che per \(n=k,k+1, \cdots \) valgono le seguenti formule:

\[ \begin{array}{l} P(T_{k} \le n)= \sum\limits_{j \ge k}{}P(N_{n}= j)= \sum\limits_{j=k}^{n}\binom{n}{j}p^{j}q^{n-j} \\ P(T_{k} = n)= pP(N_{n-1}= k-1) = \binom{n-1}{k-1}p^{k}q^{n-k} \\ \end{array} \]

Altri processi stocastici molto importanti sono ad esempio i processi di Poisson e i processi Gaussiani. Per approfondire vedere ad esempio il testo di Parzen ^[3].

3) Matrici stocastiche e regolari

Definizione 3.1 – Vettore probabilità
Un vettore riga \((u_{1},u_{2}, \cdots,u_{n}) \in \mathbb{R}^{n}\) si dice vettore probabilità o vettore stocastico se \(0 \le u_{k} \le 1 \) e \(\sum\limits_{k=1}^{n}u_{k}=1\).
La stessa definizione vale per i vettori colonna.

Esempio 3.1

\[ \begin{array}{l} v_{1}=\left(\frac{1}{3}, \frac{1}{6},\frac{1}{2}\right) \\ v_{2}=\left(\frac{1}{6}, 0, \frac{5}{6}\right) \\ \end{array} \]

Definizione 3.2 – Matrice stocastica
Una matrice quadrata \(P=(p_{ij})\) si chiama matrice stocastica destra se ognuna delle sue righe è un vettore probabilità; cioè tutti gli elementi della matrice sono non negativi e la somma di ogni riga è uguale a \(1\).
Una matrice quadrata \(P=(p_{ij})\) si chiama matrice stocastica sinistra se ognuna delle sue colonne è un vettore probabilità.
Una matrice si dice doppiamente stocastica se è sia destra sia sinistra. Nel seguito, salvo precisazione contraria, con matrice socratica intenderemo matrice stocastica destra e con vettore stocastico intenderemo vettore riga.

Esempio 3.2 – Matrice stocastica destra

\[ \begin{pmatrix} \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{4} & 0 & \frac{3}{4} \\ \end{pmatrix} \]

Teorema 3.1
Sia \(A(n \times n)\) una matrice stocastica e sia \(v \in \mathbb{R}^{n}\) un vettore di probabilità. Allora anche il vettore riga \(w=vA\) è un vettore stocastico.

Dimostrazione
Il seguente esempio concreto è utile per capire la dimostrazione generale.

\[ \begin{pmatrix} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \end{pmatrix} \cdot \begin{pmatrix} \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{4} & 0 & \frac{3}{4} \\ \end{pmatrix} = \begin{pmatrix} \frac{13}{36} & \frac{1}{9} &\frac{19}{36} \end{pmatrix} \]

Per la dimostrazione basta svolgere il prodotto del vettore con la matrice e quindi sommare i valori ottenuti, tenendo conto che la somma degli elementi del vettore e di ognuna delle righe della matrice è sempre uguale ad \(1\).
Più in generale vale il seguente teorema:

Teorema 3.2
Siano \(A(n \times n)\) e \(B(n \times n)\) due matrici stocastiche. Allora anche la matrice prodotto \(C = A \times B\) è una matrice stocastica.
In particolare ogni potenza \(A^{n}\) di una matrice stocastica è ancora una matrice stocastica.

Definizione 3.3 – Matrice regolare
Una matrice stocastica \(A\) si dice regolare se esiste un intero positivo \(n\) tale che la matrice potenza \(A^{n}\) ha tutti gli elementi positivi.

Esercizio 3.1
Verificare la regolarità delle seguenti due matrici.

\[ A= \begin{pmatrix} 0 & 1 \\ \frac{1}{4} & \frac{3}{4} \\ \end{pmatrix} \ ,\quad B= \begin{pmatrix} 1 & 0 \\ \frac{1}{4} & \frac{3}{4} \\ \end{pmatrix} \]

Definizione 3.4 – Punto fisso
Un vettore riga non nullo \(v\) è un punto fisso per una matrice \(A\) se risulta

\[ vA = v \]

In altri termini un punto fisso è un autovetture con autovalore sinistro uguale ad \(1\).

Esempio 3.3
Verificare che il vettore \(v=\left(-\frac{1}{2},1\right)\) è un punto fisso della seguente matrice:

\[ A= \begin{pmatrix} 3 & 2 \\ 1 & 2 \\ \end{pmatrix} \]

Esercizio 3.2
Dimostrare che se \(v\) è un punto fisso per una matrice \(A\), allora qualunque multiplo \(\lambda v\), con \(\lambda\) numero reale diverso da zero, è un punto fisso.

Il teorema seguente descrive le proprietà dei punti fissi di una matrice regolare.

Teorema 3.3
Sia \(P\) una matrice stocastica regolare. Allora

• \(P\) ha un unico vettore di probabilità fisso \(w\), le cui componenti sono tutte positive;
• la successione di potenze \(P,P^{2},P^{3},\cdots\) tende ad una matrice \(W\), le cui righe sono quali al vettore w;
• se \(v\) è un vettore stocastico, allora la successione \(vP,vP^{2},vP^{3},\cdots\) tende al vettore fisso w.

Nota
Ricordiamo che con la notazione \(P^{n} \to Q\) intendiamo che ogni elemento della matrice \(P^{n}\), che è un numero reale, tende all’elemento corrispondente della matrice \(Q\).

Per una dimostrazione vedere il testo di Kemeny-Snell ^[4].

Esercizio 3.3
Trovare il punto fisso della matrice regolare

\[ P= \begin{pmatrix} 0 & 1 \\ \frac{1}{4} & \frac{3}{4} \\ \end{pmatrix} \]

Quindi determinare la matrice \(Q\) cui tende la successione delle potenze \(P^{n}\).

Suggerimento
Risolvere il sistema

\[ (x,1-x) \cdot \begin{pmatrix} 0 & 1 \\ \frac{1}{4} & \frac{3}{4} \\ \end{pmatrix} = (x,1-x) \]

4) Le catene di Markov su uno spazio numerabile

Definizione 4.1 – Catena di Markov
Sia \((\Omega,\mathfrak{F},P)\) uno spazio di probabilità. Sia \(S\) un insieme finito o numerabile di stati. Consideriamo un processo stocastico discreto \(\{X_{n}, n \in \mathbb{N}\}\), dove \(\mathbb{N}=\{0,1,2,\cdots\}\), che assume valori nello spazio di stati \(S\).
Le \(X_{n}\) sono quindi variabili aleatorie tali che, per ogni \(n \in \mathbb{N}\) e \(\omega \in \Omega\), il valore della variabile aleatoria \(X_{n}(\omega)\) è un elemento dell’insieme degli stati \(S\), e indica lo stato del processo al tempo \(n\).
Il processo stocastico \(\{X_{n}: n \in \mathbb{N}\}\) è una catena di Markov se vale la seguente relazione:

\[ P(X_{n+1} |X_{0},X_{1}, \cdots,X_{n})= P(X_{n+1}|X_{n}) \]

per tutti gli \(n \in \mathbb{N}\).
Nella formula precedente l’uguaglianza deve valere per tutti i valori che ognuna delle variabili aleatorie \(X_{k}\) può assumere.
Una catena di Markov è quindi un processo stocastico discreto nei parametri e negli stati, dove la distribuzione di probabilità di \(X_{n+1}\) dello stato successivo dipende esclusivamente dallo stato attuale (proprietà dell’assenza di memoria) e non dagli stati precedenti.
In molte situazioni possiamo considerare l’indice \(n\) come il tempo. Quindi la notazione \(X_{n}=k\) indica che al tempo \(n\) il sistema è nello stato \(k\).
La quantità \(P_{i,j}=P(X_{n+1}=j|X_{n}=i)\) si chiama probabilità di transizione fra due stati, cioè di passare dallo stato \(i\) allo stato \(j\).

Definizione 4.2 – Catena di Markov omogenea
In generale la probabilità di transizione \(P_{i,j}\) dipende dagli stati e anche dal parametro \(n\). In questo articolo consideriamo il caso semplificato in cui le probabilità di transizione fra due stati sono indipendenti dal tempo, cioè da \(n\). In questo caso la catena di Markov si dice omogenea.
Quindi per una catena di Markov omogenea l’evoluzione del processo è determinata dall’equazione

\[ P_{i,j}= P(X_{n+1}=j|X_{n}=i) \ ,\quad i,j \in S \]

In una catena di Markov lo spazio degli stati può essere finito \(S=\{1,2,\cdots, M\}\), oppure infinito numerabile, che possiamo identificare con l’insieme dei numeri naturali \(\mathbb{N}=\{0,1,2,\cdots\}\).
In molte applicazioni nella teoria delle code si utilizzano catene di Markov con un numero infinito di stati. Ad esempio uno stato spesso rappresenta il numero di clienti in coda per un dato servizio. Altri esempi sono i cammini casuali, che vedremo in seguito.
La distribuzione di probabilità della catena di Markov al tempo \(t=0\), cioè la distribuzione di probabilità della variabile aleatoria \(X_{0}\), si chiama distribuzione iniziale.
L’evoluzione di una catena di Markov omogenea è completamente determinata dalla distribuzione iniziale e dalle probabilità di transizione \(P_{i,j}\).

Nota
La definizione delle catene di Markov può essere estesa al caso in cui l’insieme dei parametri non è numerabile. In tal caso si parla di processo di Markov:

\[ P (Y_{t+s}=j|Y_{u}: u \le t)=P(Y_{t+s}=j|Y_{t}) \]

Se la probabilità condizionale non dipende da \(t\) allora il processo si dice omogeneo nel tempo.
Anche lo spazio degli stati può essere non numerabile. Vedremo alcuni esempi di applicazioni dei processi di Markov in un articolo successivo dedicato alla teoria delle Code.

4.1) Matrice di transizione

Per rappresentare una catena di Markov si possono usare vettori e matrici. Se lo spazio degli stati è finito allora si utilizzano vettori e matrici di ordine finito.
Se invece lo spazio degli stati è infinito numerabile allora le somme verranno sostituite da serie, e le matrici quadrate di ordine finito verrano sostituite da matrici infinite.
In questo articolo studieremo prevalentemente catene di Markov con un numero finito di stati.

Definizione 4.3 – Matrice di transizione
Sia \(\{X_{n}: n =0,1,2,\cdots\}\) una catena di Markov, con spazio degli stati finito \(S=\{0,1,2,\cdots, M\}\).
La matrice di transizione \(P\) è la seguente:

\[ P = \begin{pmatrix} P_{0,0} & P_{0,1} & \cdots & P_{0,M} \\ P_{1,0} & P_{1,1} & \cdots & P_{1,M} \\ \vdots & & \ddots & \vdots \\ P_{M,0} & P_{M,1} & \cdots & P_{M,M} \\ \end{pmatrix} \]

Esercizio 4.1
Dimostrare che la matrice di transizione è una matrice stocastica. Cioè

\[ \begin{array}{l} P_{i,j} \ge 0 \\ \sum\limits_{j} P_{i,j}= 1 \ ,\quad i=0,1,\cdots,M \end{array} \]

Gli elementi di ogni riga quindi hanno somma uguale ad \(1\) (matrice stocastica destra).

4.2) Grafo di transizione di una catena di Markov finita

Un modo alternativo di rappresentare una catena di Markov finita consiste nel creare un grafo orientato con le seguenti regole:

• i vertici del grafo rappresentano gli stati \(1,2,\cdots,M\);
• due vertici \(i,j\) sono connessi da un arco orientato solo se c’è una probabilità positiva di transizione dallo stato \(i\) allo stato \(j\). Il valore della probabilità viene usato come etichetta dell’arco.

Questo grafo viene anche chiamato grafo di transizione.

Esempio 4.1

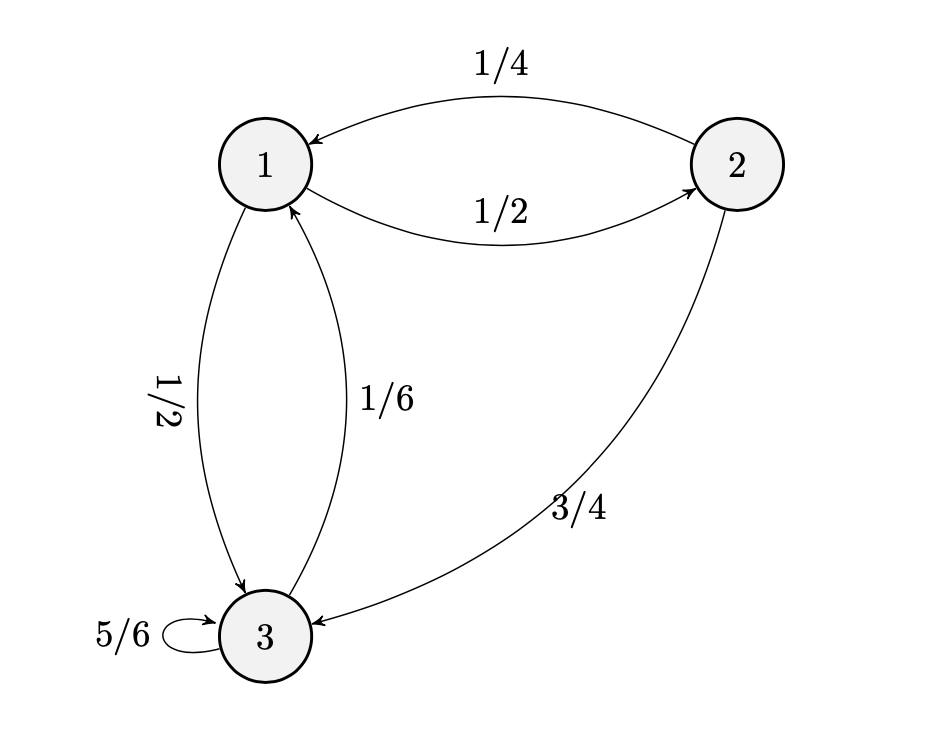
Esercizio 4.2
Ricavare la matrice di transizione corrispondente al grafo precedente.

4.3) Dinamica delle catene di Markov – Equazioni di Chapman-Kolmogorov

Ricordando la definizione di probabilità condizionata, è facile dimostrare il seguente teorema:

Teorema 4.1

\[ P(X_{n+1}=i_{1},\cdots,X_{n+m}=i_{m}|X_{n}=i_{0})=P_{i_{0},i_{1}}P_{i_{1},i_{2}}\cdots P_{i_{m-1},i_{m}} \]

Se poniamo \(n=0\) abbiamo il seguente importante risultato:

Corollario 4.1
Sia \(\pi\) la distribuzione iniziale sullo spazio degli stati \(S\), e sia

\[ P(X_{0}=i)= \pi(i) \quad \forall i \in S \]

Allora

\[ P(X_{0}=i_{0},X_{1}=i_{1},\cdots,X_{m}=i_{m})= \pi(i_{0})P_{i_{0},i_{1}}P_{i_{1},i_{2}}\cdots P_{i_{m-1},i_{m}} \]

Quindi la distribuzione congiunta delle variabili aleatorie \(\{X_{0},X_{1},\cdots,X_{m}\}\) è completamente determinata dalla distribuzione iniziale \(\pi\) e dalla matrice di transizione \(P\).

Un problema fondamentale nella teoria delle catene di Markov è quello di calcolare la probabilità di transizione da uno stato \(i\) allo stato \(j\), dopo \(m\) passi. Indichiamo questa probabilità con il simbolo \(P_{i,j}(m)\). I coefficienti della matrice di transizione corrispondono al caso \(m=1\), cioè \(P_{i,j}(1)\).
Consideriamo inizialmente il caso \(m=2\), cioè una transizione di due passi.

Teorema 4.2

\[ P_{i,j}(2)=P(X_{n+2}=j|X_{n}=i) = (P^{2})_{i,j} \]

dove il simbolo \((P^{2})_{i,j}\) indica l’elemento \((i,j)\) della matrice di transizione elevata al quadrato, cioè di \(P^{2}=P \cdot P\).

Suggerimento
Partire dalla seguente formula

\[ \begin{array}{l} P(X_{n+2}=j|X_{n}=i) = \sum\limits_{k \in S} P(X_{n+2}=j \land X_{n+1}=k|X_{n}=i) \end{array} \]

e applicare la definizione di probabilità condizionata.
Più in generale vale il seguente teorema:

Teorema 4.3

\[ P(X_{m+n}=j|X_{n}=i) = (P^{m})_{i,j} \ ,\quad i,j \in S , n \in \mathbb{N} \]

Se \(m=0\) allora \(P^{0}=I\), cioè la matrice identità.
Quindi per calcolare la probabilità di passare dallo stato \(i\) allo stato \(j\) in \(m\) passi, basta calcolare la potenza della matrice di transizione \(P^{m}\). La probabilità cercata è l’elemento \((i,j)\) della matrice potenza.

Teorema 4.4 – Equazioni Chapman-Kolmogorov

\[ ( P^{m+n})_{i,j}=\sum\limits_{k \in S}{}(P^{m})_{i,k}(P^{n})_{k,j} \ ,\quad i,j \in S \]

Dimostrazione
Il teorema segue direttamente dalla seguente uguaglianza di matrici:

\[ P^{m+n}=P^{m}P^{n} \ ,\quad m,n \in \mathbb{N} \]

Possiamo scrivere le equazioni di Chapman-Kolmogorov nella seguente forma estesa equivalente:

\[ P(X_{m+n}=j|X_{0}=i) =\sum\limits_{k \in S}{} P(X_{n}=j|X_{0}=k) P(X_{m}=k|X_{0}=i) \ ,\quad i,j \in S \]

Esercizio 4.3
Sia data la matrice di transizione

\[ P = \begin{pmatrix} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 \\ \frac{1}{4} & \frac{1}{4} & 0 & \frac{1}{2} \\ 0 & \frac{1}{2} & 0 & \frac{1}{2} \\ \end{pmatrix} \]

Calcolare la matrice di transizione dopo \(2\) passi.

Soluzione:

\[ P^{2}= \begin{pmatrix} \frac{13}{36} & \frac{13}{36} & \frac{1}{9} & \frac{1}{6} \\ \frac{5}{12} & \frac{5}{12} & \frac{1}{6} & 0 \\ \frac{5}{24} & \frac{11}{24} & \frac{1}{12} & \frac{1}{4} \\ \frac{1}{4} & \frac{1}{2} & 0 & \frac{1}{4} \\ \end{pmatrix} \]

5) Classificazione degli stati

5.1) Decomposizione dello spazio degli stati

Definizione 5.1
Dati due stati \(i,j\), lo stato \(j\) si dice accessibile dallo stato \(i\) se

\[ (P^{n})_{i,j}=P(X_{n}=j|X_{0}=i) \gt 0 \]

per qualche \(n \ge 0\).
Due stati \(i,j\) si dicono comunicanti se ognuno è accessibile dall’altro.

Esercizio 5.1
Dimostrare che la comunicabilità fra due stati è una relazione di equivalenza, cioè riflessiva, simmetrica e transitiva.

Come è noto una relazione di equivalenza su un insieme determina una partizione dell’insieme. Quindi ogni catena di Markov può essere partizionata in classi di stati disgiunte. Due stati appartengono alla stessa classe se e solo se comunicano tra loro.
Lo spazio degli stati può essere quindi scritto come unione di classi disgiunte:

\[ S = C_{1} \cup C_{2}\cup \cdots \cup C_{r} \ ,\quad 1 \le r \le \infty \]

Le classi \(C_{k}\) sono insiemi non vuoti. Una classe \(C_{k}\) si dice chiusa se, per ogni \(x \in C_{k}\) e \(y \not \in C_{k}\) , allora \(y\) non è accessibile da \(x\).

Un catena di Markov si dice irriducibile se consiste in una sola classe di equivalenza, cioè se tutti gli stati comunicano fra loro. In caso contrario si dice riducibile.

5.2) Ricorrenza

Definizione 5.2
Dato uno stato \(j\), definiamo con \(T_{j}^{r}\) il tempo di primo ritorno allo stato \(j\):

\[ \begin{array}{l} T_{j}^{r}= \{\inf n \ge 1 : X_{n}=j\} \\ T_{j}^{r}= \infty \quad \text{se } X_{n} \neq j \quad \forall n \ge 1 \end{array} \]

Definizione 5.3
Uno stato \(j \in S\) si dice ricorrente, se partendo dallo stato \(j\) il processo ritornerà, con probabilità uguale a \(1\), allo stesso stato \(j\) dopo un numero finito di passi. In simboli se

\[ P(T_{j}^{r} \lt \infty| X_{0}=j)=1 \]

In modo equivalente esiste un \(n \ge 1\) tale che

\[ P(X_{n}=j, n \ge 1| X_{0}=j)=1 \]

Esercizio 5.2
Dimostrare che se uno stato è ricorrente, allora il numero di ritorni è quasi certamente (in inglese almost surely, in simboli a.s.) infinito, cioè con probabilità = \(1\).

Esercizio 5.3
Dimostrare che se uno stato \(j \in S\) è ricorrente, allora ogni stato \(i \in S\) che comunica con \(j\) è anche esso ricorrente.

Definizione 5.4
Uno stato ricorrente \(j \in S\) si dice ricorrente positivo se il tempo medio di ritorno è finito, cioè se

\[ E(T_{j}^{r}|X_{0}=i) \lt \infty \]

Se il tempo medio di ritorno è infinito allora si dice che è uno stato ricorrente nullo.

Definizione 5.5
Uno stato \(j\) si dice transiente se non è ricorrente, cioè se

\[ P(T_{j}^{r} \lt \infty|X_{0}=j) \lt 1 \]

oppure

\[ P(T_{j}^{r} = \infty|X_{0}=j) \gt 0 \]

Definizione 5.6 – Periodo di uno stato
Il periodo \(d(j)\) di uno stato \(j\) è il massimo comune divisore \(\text{(gcd)}\) dei valori di \(n\) per i quali risulta \(( P^{n})_{j,j} \gt 0\):

\[ d(j)= \{\text{gcd } ({n \ge 1 : (P^{n})_{j,j} \gt 0})\} \]

Se il periodo è uguale ad \(1\) allora lo stato si dice aperiodico, altrimenti si dice periodico.

Teorema 5.1
Per ogni catena di Markov finita o numerabile tutti gli stati di una classe hanno lo stesso periodo.

Definizione 5.7
Uno stato si dice ergodico se è aperiodico e ricorrente positivo. Una catena di Markov si dice ergodica se lo sono tutti gli stati.

Definizione 5.8
Uno stato \(j\) si dice assorbente se \(P_{j,j}=1\).
Chiaramente uno stato assorbente è aperiodico e ricorrente.

La seguente tabella contiene un riepilogo dei vari tipi di stati.

\[ \begin{array}{|l|c|} \hline \textbf{Tipo di stato } & \textbf{Formula} \\ \hline \text{Stato Ricorrente } & P(T_{j}^{r} \lt \infty|X_{0}=j)=1 \\ \hline \text{Stato Ricorrente positivo } & E(T_{j}^{r}|X_{0}=j) \lt \infty \\ \hline \text{Stato Ricorrente nullo } & E(T_{j}^{r}|X_{0}=j) = \infty \\ \hline \text{Stato transiente } & P(T_{j}^{r} \lt \infty|X_{0}=j) \lt 1 \\ \hline \text{Stato assorbente } & P_{j,j}=1 \\ \hline \text{Stato periodico } & \text{Periodo } \gt 1 \\ \hline \text{Stato aperiodico } & \text{Periodo } =1 \\ \hline \text{Stato ergodico } & \text{Aperiodico e ricorrente positivo} \\ \hline \end{array} \]

Esercizio 5.4
Determinare le classi di stati e classificare gli stati \(\{0,1,2,3\}\) della seguente matrice di transizione:

\[ P = \begin{pmatrix} 0.7 & 0 & 0.3 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0.2 & 0.3 & 0 & 0.5 \\ \end{pmatrix} \]

Soluzione: \([C_{1}=\{0,2\}, C_{2}=\{1\},C_{3}=\{3\};\text{stati ricorrenti:}\{0,2\}, \text{stati transienti:}\{1,3\}]\)

6) Comportamento asintotico di una catena di Markov

Definizione 6.1
Una catena di Markov \(\{X_{n}, n \in \mathbb{N}\}\) si dice che ammette una distribuzione limite di probabilità se sono soddisfatte le seguenti due condizioni:

• esiste il limite \(\lim\limits_{n \to \infty}P(X_{n}=j|X_{0}=i)\) per tutti gli \(i,j \in S\);
• questi valori limiti formano una distribuzione di probabilità, cioè per tutti gli \(i \in S\) si ha

\[ \sum\limits_{j \in S}\lim\limits_{n \to \infty}P(X_{n}=j|X_{0}=i)=1 \]

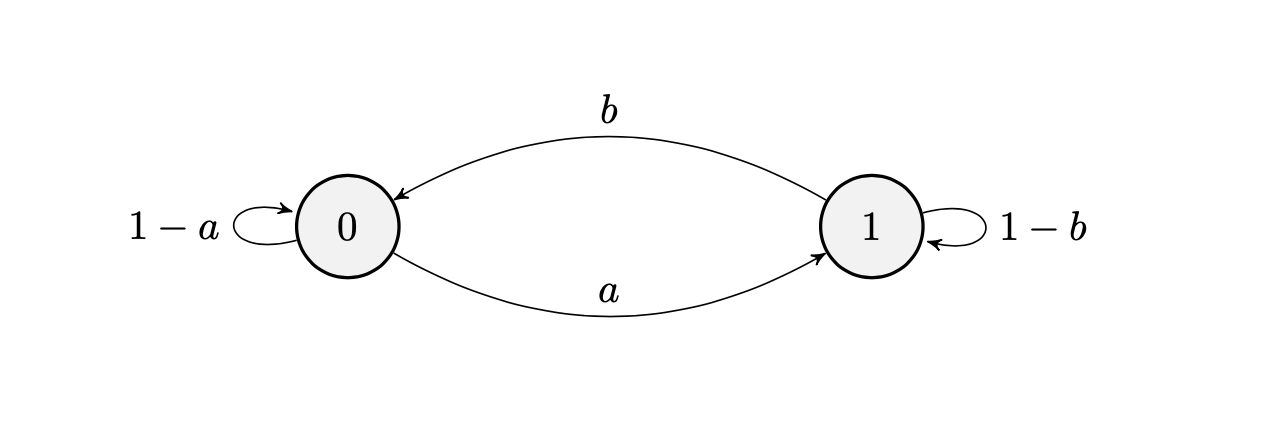
Esempio 6.1 – Catena di Markov a due stati
Consideriamo ua catena di Markov con la seguente matrice di transizione:

\[ P = \begin{pmatrix} 1-a & a \\ b & 1 -b \\ \end{pmatrix} \]

dove \(0 \le a \le 1\) e \(0 \le b \le 1\).
La rappresentazione grafica è la seguente:

Mediante il metodo di induzione si può dimostrare il seguente teorema:

Teorema 6.1

\[ \begin{array}{l} P^{n} = \dfrac{1}{a+b} \begin{pmatrix} b+ a(1-a-b)^{n} & a(1-(1-a-b)^{n}) \\ b(1-(1-a-b)^{n}) & a+b(1-a-b)^{n} \end{pmatrix} \end{array} \]

che può essere scritto in modo equivalente:

\[ \begin{array}{l} P^{n} = \dfrac{1}{a+b} \begin{pmatrix} b & a \\ b & a \end{pmatrix} + \dfrac{(1-a-b)^{n}}{a+b} \begin{pmatrix} a & -a \\ -b & b \end{pmatrix} \end{array} \]

Esercizio 6.1
Dimostrare che nell’ipotesi \((a,b) \neq (0,0)\) e \((a,b) \neq (1,1)\) abbiamo

\[ \lim\limits_{n \to \infty}P^{n} = \frac{1}{a+b} \begin{pmatrix} b & a \\ b & a \end{pmatrix} \]

Quindi la distribuzione limite della catena a due stati è

\[ \pi = [\pi_{0},\pi_{1}]=\left(\dfrac{b}{a+b},\dfrac{a}{a+b}\right) \]

Probabilità di ritorno ad uno stato
Nello studio del comportamento asintotico delle catene di Markov un parametro importante è la probabilità \(p_{ij}\) di tornare ad uno stato \(j\), dopo aver iniziato da uno stato \(i\), in un tempo finito. Se lo stato \(j\) è transiente abbiamo il seguente teorema:

Teorema 6.2
Se una catena di Markov ha uno stato transiente \(j \in S\) allora

\[ \lim_{n \to \infty}P(X_{n}=j|X_{0}=i) = 0 \quad \forall i \in S \]

6.1) Le catene di Markov ergodiche e regolari

Indichiamo con \(\mu_{j}(j)=E(T_{J}^{r}|X_{0}=j)\) il tempo medio fra due ritorni successivi allo stesso stato \(j\). Vale il seguente teorema:

Teorema 6.3
Sia data una catena di Markov \(\{X_{n}, n \in \mathbb{N}\}\) aperiodica, irriducibile e ricorrente. Allora

\[ \lim\limits_{n \to \infty} P(X_{n}=j|X_{0}=i)=\frac{1}{\mu_{j}(j)} \]

per ogni coppia \((i,j) \in S\).

Ricordiamo che una catena di Markov si dice ergodica se ogni stato è aperiodico e ricorrente positivo. In termini equivalenti, se c’è una probabilità positiva di passare eventualmente da uno stato qualsiasi ad un altro stato.
Una catena di Markov regolare è anche ergodica, tuttavia non sempre vale il viceversa.

Esempio 6.2
Consideriamo la seguente matrice stocastica:

\[ P= \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \]

Si tratta di una catena di Markov ergodica, in quanto si può passare da ogni stato ad un altro. Tuttavia non è regolare, in quanto per ogni potenza \(P^{n}\), se \(n\) è dispari non si può passare dallo stato \(0\) allo stato \(0\) in \(n\) passi, e se \(n\) è pari non si può passare dallo stato \(0\) allo stato \(1\) in \(n\) passi.

6.2) Distribuzione stazionaria di una catena di Markov

Definizione 6.2
Una distribuzione di probabilità \(\pi \) sull’insieme deli stati \(S\) si dice stazionaria se è un punto fisso della catena di Markov, cioè

\[ \pi P = \pi \]

In altre parole il vettore \(\pi\) è invariante rispetto alla matrice di transizione \(P\) della catena di Markov.
Il concetto di distribuzione stazionaria non va confuso con quello di distribuzione limite. Se una catena di Markov inizia con una distribuzione stazionaria allora rimarrà sempre nella stessa distribuzione, al passare del tempo, cioè

\[ \begin{array}{l} P(X_{0}=j)= P(X_{1}=j) \quad \forall j \in S \end{array} \]

La distribuzione limite invece è una distribuzione alla quale tende la catena di Markov, a partire da una distribuzione iniziale qualsiasi.

Vale il seguente teorema:

Teorema 6.4
Sia data una catena di Markov \(X_{n}\) che soddisfa le seguenti condizioni:

• ergodica, cioè aperiodica e con ricorrenza positiva
• irribucibile

Allora esiste la distribuzione limite

\[ \pi_{j}=\lim_{n \to \infty}P(X_{n}=j|X_{0}=i)=\lim_{n \to \infty}(P^{n})_{i,j}= \frac{1}{\mu_{j}(j)} \]

Questa distribuzione limite è una distribuzione strazionaria, cioè

\[ \pi = \pi P \]

Nel caso di una catena di Markov con spazio degli stati finito, tutti gli stati ricorrenti sono ricorrenti positivi. Quindi per l’esistenza delle distribuzione stazionaria è sufficiente che sia aperiodica e irriducibile.

Esercizio 6.2
Consideriamo la catena di Markov con spazio degli stati \(S=\{0,1,2,\cdots\}\) e matrice di transizione \(P\):

\[ P = \begin{pmatrix} q & p & \cdots & & \\ q & 0 & p & \cdots & \\ 0 & q & 0 & p & \cdots \\ \vdots \\ & 0 & \cdots \\ \end{pmatrix} \]

Verificare che la catena è irriducibile e aperiodica. Osserviamo che c’è un loop sullo stato \(0\).

Per verificare se esiste una distribuzione stazionaria \(\pi = \pi P\), dovremo risolvere un sistema infinito di equazioni:

\[ \begin{cases} \pi_{0}= \pi_{0}q + \pi_{1}q \\ \pi_{1}= \pi_{0}p + \pi_{2}q \\ \pi_{2}= \pi_{1}p + \pi_{3}q \\ \cdots \end{cases} \]

Se un vettore \(\pi\) è soluzione, allora lo è anche un multiplo costante \(c\pi\). Poniamo quindi \(\pi_{0}=1\) e risolviamo. Abbiamo

\[ \pi = \left(1, \frac{p}{q}, \frac{p^{2}}{q^{2}}, \frac{p^{3}}{q^{3}}, \cdots \right) \]

Discutere i casi \(p \ge q\) e \(p \lt q\).

6.3) Catene di Markov su spazi di stati finiti

Se lo spazio degli stati è un insieme finito, la teoria delle catene di Markov è più semplice.

Teorema 6.5
In una catena di Markov finita, gli stati di una classe sono tutti ricorrenti oppure tutti transienti.

Dimostrazione
Supponiamo che lo stato \(i\) sia transiente, e quindi esiste nella stessa classe uno stato \(j\) tale che \(i \rightarrow j\) ma \(j \not \rightarrow i\). Supponiamo ora che \(k\) sia un altro stato della stessa classe di \(i\). Abbiamo \(k \rightarrow i\) e \(i \rightarrow j\), da cui \(k \rightarrow j\). Se fosse possibile \(j \rightarrow k\) allora ci sarebbe un cammino per arrivare da \(j\) allo stato \(i\), contro l’ipotesi. Quindi lo stato \(k\) è transiente. Quindi gli stati di una classe sono tutti transienti oppure tutti ricorrenti.

Esercizio 6.3
Dimostrare che una catena di Markov finita ha almeno una classe ricorrente, cioè formata solo da stati ricorrenti.

Quindi l’insieme degli stati di una catena di Markov finita può essere decomposto in questo modo:

\[ S = T \cup C_{1} \cup C_{2}\cup \cdots \cup C_{r} \ ,\quad 1 \le r \lt \infty \]

dove \(T\) è un insieme (eventualmente vuoto) di stati transienti e le classi \(C_{k}\) sono classi chiuse, irriducibili e formate solo da stati ricorrenti.

Teorema 6.6
In una catena di Markov finita ogni stato ricorrente è ricorrente positivo.

Una catena di Markov finita irriducibile e aperiodica è regolare. Vale il seguente teorema:

Teorema 6.7
Ogni catena di Markov finita irriducibile e aperiodica ha una unica distribuzione stazionaria \(\pi\) tale che \(\pi=\pi P\).

Esempio 6.3
Consideriamo la catena di Markov con spazio degli stati \(S=\{0,1\}\) e matrice di transizione

\[ P= \begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{2}{5} & \frac{3}{5} \\ \end{pmatrix} \]

Dimostrare che la distribuzione stazionaria è \(\pi=\left(\dfrac{4}{9},\dfrac{5}{9}\right)\).

Esercizio 6.4
Supponiamo di lanciare un dado \(n\) volte. Indichiamo con \(X_{n}\) il numero più grande ottenuto nelle prime \(n\) prove. Determinare lo spazio degli stati \(S\) e la matrice di transizione. Verificare se esistono stati assorbenti. Inoltre dimostrare che non esiste una distribuzione stazionaria.

Soluzione:

\[ P= \begin{pmatrix} \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} &\frac{1}{6} & \frac{1}{6}\\ 0 & \frac{2}{6} & \frac{1}{6} & \frac{1}{6} &\frac{1}{6} & \frac{1}{6} \\ 0 & 0 & \frac{3}{6} & \frac{1}{6} &\frac{1}{6} & \frac{1}{6} \\ 0 & 0 & 0 & \frac{4}{6} &\frac{1}{6} & \frac{1}{6} \\ 0 & 0 & 0 & 0 &\frac{5}{6} & \frac{1}{6} \\ 0 & 0 & 0 & 0 &0 & \frac{6}{6} \\ \end{pmatrix} \]

7) Esempi di catene di Markov

7.1) Processo di Bernoulli – Numero di successi

Indichiamo con \(N_{n}\) il numero di successi in \(n\) prove di Bernoulli. Lo spazio di stati è infinito numerabile \(S=\{0,1,2,\cdots \}\).
Il numero dei successi in \(n\) prove dipende solo dal numero dei successi in \(n-1\) prove, quindi il processo stocastico \(\{N_{n}: n \ge 0\}\) è una catena di Markov omogenea.
La distribuzione di probabilità degli stati è

\[ P_{i,j}=P(N_{n+1}=j|N_{n}=i) = \begin{cases} p \quad \text{se } j=i+1 \\ q \quad \text{se } j=i \\ 0 \quad \text{altrimenti} \end{cases} \]

La matrice di transizione è la seguente:

\[ P = \begin{pmatrix} q & p & & & & 0 \\ & q & p & & & \\ & & q & p & & \\ & & & \cdot & \cdot & \\ & & & & \cdot &\cdot \\ 0 & & & & & \cdot \\ \end{pmatrix} \]

È una catena irregolare e non ha una distribuzione stazionaria.

Esercizio 7.1

\[ P_{i,j}(n)=\binom{n}{j-i}p^{j-i}q^{n-j+i} \ ,\quad j=i,i+1, \cdots, n+i \]

7.2) Processo di Bernoulli – Tempo di attesa per l’n-esimo successo

Indichiamo con \(T_{n}\) il tempo di attesa per l’ennesimo successo in un processo di Bernoulli. Il processo stocastico \(\{T_{n}: n \ge 0\}\) è una catena di Markov in quanto si ha 

\[ P(T_{k+1}=n|T_{0}, \cdots,T_{k})= P(T_{k+1}=n|T_{k}) \ ,\quad n \ge k \]

per ogni \(T_{0},\cdots,T_{k-1}\).
Infatti, poiché le prove di Bernoulli sono indipendenti abbiamo

\[ P(T_{k+1}=n|T_{0}, \cdots,T_{k})= \begin{cases} pq^{n-1-T_{k}} \quad \text{se } T_{k} \lt n \\ 0 \quad \text{se } T_{k} \ge n \\ \end{cases} \]

In modo equivalente possiamo scrivere

\[ P(T_{n+1}=j|T_{n}=i)= \begin{cases} pq^{j-i-1} \quad \text{se } j \ge i+1 \\ 0 \quad \text{altrimenti } \\ \end{cases} \]

La matrice di transizione è

\[ P = \begin{pmatrix} 0 & p & pq & pq^{2} & pq^{3} & \cdot & \cdot & \cdot \\ & 0 & p & pq & pq^{2} & \cdot & \cdot & \cdot \\ & & 0 & p & pq & \cdot & \cdot & \cdot \\ & & & 0 & p & \cdot & \cdot & \cdot \\ & & & & & \cdot & \cdot & \cdot \\ 0 & \cdots \\ \end{pmatrix} \]

7.3) Modello di Bernoulli-Laplace

Due urne contengono in totale \(2N\) palline, la metà bianche e l’altra metà nere. Indichiamo con \(X_{n}\) il numero di palline bianche presentI nella prima urna al tempo \(n\).
Al tempo \(t=0\) nella prima urna ci sono \(X_{0}=k\) palline bianche e \(N-k\) palline nere, mentre nella seconda urna ci sono \(k\) palline nere e \(N-k\) palline bianche. Ad ogni prova si estrae a caso una pallina da ognuna delle due urne e le due palline vengono scambiate.
Diciamo che il sistema si trova nello stato \(S_{k}, \ k =0,1,\cdots,N\) se la prima urna contiene \(k\) palline bianche, e quindi \(N-k\) palline nere.
Dimostrare che le probabilità di transizione sono le seguenti:

\[ \begin{array}{l} P_{k,k-1}= \left(\dfrac{k}{N}\right)^{2} \ ,\quad 1 \le k \le N-1 \\ P_{k,k+1}= \left(\dfrac{N-k}{N}\right)^{2} \ ,\quad 1 \le k \le N-1 \\ P_{k,k}= 2 \dfrac{k(N-k)}{N^{2}} \ ,\quad 1 \le k \le N-1 \\ P_{k,j} = 0 \text{ se } |k-j| \gt 1 \ ,\quad k=0,1,\cdots,N \end{array} \]

7.4) Somma di variabili aleatorie indipendenti

Supponiamo che \(X_{1},X_{2},\cdots\) siano variabili aleatorie discrete indipendenti e identicamente distribuite, con distribuzione \(\{p_{k}=P(X_{i}=k), k=0,1,\cdots\}\). Consideriamo la somma

\[ Z_{n} = \begin{cases} 0 \quad \text{se } n = 0 \\ X_{1}+X_{2}+ \cdots + X_{n} \quad \text{se } n \ge 1 \end{cases} \]

Abbiamo \(Z_{n+1}=Z_{n}+ X_{n+1}\), e poiché le \(X_{n}\) sono indipendenti si ha

\[ P(Z_{n+1}=j|Z_{0},Z_{1}, \cdots,Z_{n}) = P(X_{n+1}=j – Z_{n}|Z_{0},Z_{1},\cdots,Z_{n})=p_{j-Z_{n}} \]

Il processo \(Z_{n}\) è quindi una catena di Markov. Le probabilità di transizione sono \(P_{i,j}=p_{j-i}\) e la matrice di transizione è

\[ P = \begin{pmatrix} p_{0} & p_{1} & p_{2} & p_{3} & \cdot & \cdot & \cdot \\ & p_{0} & p_{1} & p_{2} & \cdot & \cdot & \cdot \\ & & p_{0} & p_{1} & \cdot & \cdot & \cdot \\ & & & p_{0} & \cdot & \cdot & \cdot \\ & & & & \cdot & \cdot & \cdot \\ & & & & & \cdot & \cdot \\ \end{pmatrix} \]

7.5) Moto casuale semplice senza vincoli

Un moto casuale sugli interi \(\mathbb{Z}\) è un cammino che parte dal punto \(0\), si muove a destra di un passo di lunghezza \(1\) con probabilità \(p\) e a sinistra di un passo \(1\) con probabilità \(q=1-p\). Se \(p=0,5\) il moto casuale si dice simmetrico.
È un caso particolare della somma di variabili aleatorie indipendenti e identicamente distribuite, discusso nel paragrafo precedente. In questo caso le \(X_{n}\) sono variabili di Bernoulli:

\[ \begin{equation} \begin{cases} P(X_{n}=1)= p \\ P(X_{n}=-1) = 1-p \end{cases} \end{equation} \]

dove \(p+q=1\).

Per ogni intero positivo \(n\) definiamo la somma \(S_{n}\):

\[ S_{n}=X_{1}+ X_{2}+ \cdots + X_{n} \ ,\quad n \ge 1 \]

La successione \(S_{n}\) è una catena di Markov discreta, con spazio degli stati \(S=\{\cdots,-2,-1,0,1,2,\cdots\}\).
La matrice di transizione si trova facilmente utilizzando la formula

\[ P(S_{n+1}=j|S_{n}=i)=P(X_{n+1}=j-i) \]

Esercizio 7.2

\[ \begin{array}{l} E(S_{n}|S_{0}=0)= n(p-q) \\ Var(S_{n}|S_{0}=0)=4npq \end{array} \]

7.6) Moto casuale con barriere riflettenti

Un moto casuale può essere limitato da barriere che impediscono di proseguire in una data direzione. Una barriera può essere assorbente se una volta arrivato il moto si arresta. Può essere riflettente se il moto continua nella direzione opposta.
La matrice di transizione per il moto casuale con barriere riflettenti è la seguente:

\[ P = \begin{pmatrix} 0 & 1 & 0 & \cdots \\ q & 0 & p & \cdots & 0 \\ & q & 0 & p \\ \vdots \\ 0 & 0 & \cdots & 1 &0 \\ \end{pmatrix} \]

7.7) Moto casuale con barriere assorbenti

Nel caso di moto casuale con barriere assorbenti, una volta raggiunta una delle barriere il moto si arresta. La matrice di transizione per il moto casuale con barriere riflettenti è la seguente:

\[ P = \begin{pmatrix} 1 & 0 & 0 & \cdots &\cdots &0 \\ q & 0 & p & \cdots &\cdots & 0 \\ & q & 0 & p &\cdots &0 \\ \vdots \\ 0 &0 & \cdots & \cdots & 0 & 1 \\ \end{pmatrix} \]

7.8) Il problema della rovina del giocatore

Il problema della rovina del giocatore può essere formulato nel seguente modo. Supponiamo di avere un giocatore \(A\) che scommette \(1\) euro contro il banco, con probabilità \(p\) di vincere un euro e probabilità \(q=1-p\) di perdere \(1\) euro.
Il capitale iniziale di \(A\) è di \(a\) euro, mentre il banco ha un capitale uguale a \(b\). La somma totale è quindi costante e uguale a \(c=a+b\). Determinare la probabilità che \(A\) vada in rovina, cioè che la somma a sua disposizione diventi uguale a zero, prima di essere uguale a \(c\).
Indichiamo con \(X_{n}\) la somma di \(A\) al tempo \(n\) e con \(Y_{n}\) la somma del banco al tempo \(n\). Quindi \(X_{0}=a\) e \(Y_{0}= b\).
Il gioco termina se \(X_{n}=0\) oppure \(X_{n}=c\).
La quantità di moneta posseduta da \(A\) al tempo \(t+1\) dipende solo dalla moneta posseduta al tempo \(t\), quindi abbiamo una catena di Markov. Abbiamo

\[ X_{n+1}=X_{n}+ Z_{n+1} \]

dove

\[ \begin{array}{l} Z_{n+1} = \begin{cases} +1 \quad \text{con probabilità } p \\ -1 \quad \text{con probabilità } 1-p \end{cases} \end{array} \]

Si tratta di un esempio di moto casuale con barriere assorbenti in \(X_{n}=0\) oppure \(X_{n}=c\).

Esercizio 7.3
Determinare la matrice di transizione relativa nel caso \(a=2\) e \(b=2\).
Abbiamo \(5\) stati, che possiamo indicare con i numeri interi: \(S=\{0,1,\cdots,4\}\). Inoltre \(p_{0,0}=p_{4,4}=1\).

Soluzione

\[ P = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 1-p & 0 & p & 0 & 0 \\ 0 & 1-p & 0 & p & 0 \\ 0 & 0 & 1-p & 0 & p \\ 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \]

Conclusione

In questo articolo abbiamo presentato alcuni concetti base delle catene di Markov. Il campo di applicazione delle catene di Markov e più in generale dei processi di Markov si estende a numerosi settori della scienza e della tecnologia. Ad esempio:

• finanza – studio dei mercati finanziari
• biologia – evoluzione di popolazioni animali, processi di nascita e morte
• motori di ricerca sul web – ad esempio l’algoritmo PageRank di Google
• ricerca operativa – teoria delle code
• studio del linguaggio naturale, per la generazione dei testi e il riconoscimento vocale

Gli studenti interessati potranno ampliare e approfondire le loro conoscenze con alcuni testi indicati nella bibliografia.

---

Bibliografia

^[1]W. Feller – An Introduction to Probability Theory (Vol. I,II – Wiley)

^[2]P. Brémaud – Discrete Probability Models and Methods (Springer)

^[3]Parzen – Stochastic Processes (Dover Books on Mathematics)

^[4]Kemeny, Snell – Finite Markov Chains (Springer UTM)