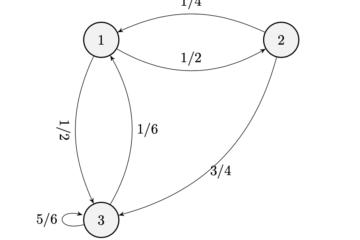
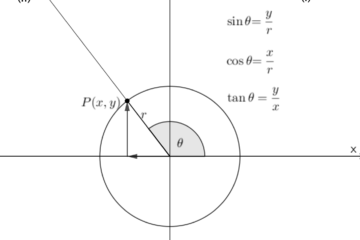
Le Serie Numeriche – Convergenza Assoluta e Condizionale, Sommazione delle Serie Divergenti
In un articolo precedente abbiamo studiato le principali proprietà delle successioni di numeri reali e complessi. Le successioni numeriche sono la base per la teoria delle serie numeriche, che studieremo in questo articolo.La teoria delle serie ha un vasto campo di applicazioni in numerosi settori della matematica pura e applicata: Leggi tutto…