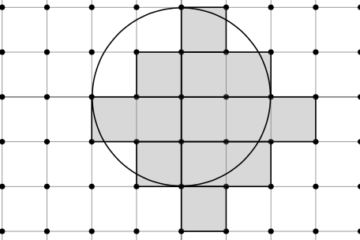
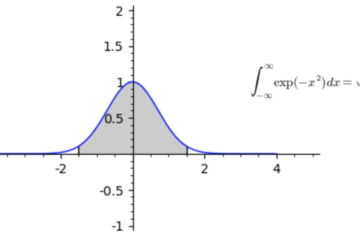
Geometria dei Numeri – Il Problema del Cerchio di Gauss
Consideriamo una regione limitata dello spazio euclideo a \(n\) dimensioni \(\mathbb{R}^{n}=\{(x_{1},x_{2}, \cdots,x_{n}): x_{k} \in \mathbb{R}\}\). La geometria dei numeri studia i punti con coordinate cartesiane intere che sono contenuti nella regione. Ad esempio nello spazio \(\mathbb{R}^{3}\) si contano i punti \((x,y,z)\) a coordinate intere contenuti in una sfera di raggio Leggi tutto…