In questo articolo studieremo le partizioni dei numeri interi positivi e, in particolare, la funzione aritmetica \(p(n)\), che conta il numero di partizioni di \(n\).
1) La teoria additiva dei numeri e le partizioni
La teoria dei numeri ha due branche fondamentali: la teoria moltiplicativa e la teoria additiva. La teoria moltiplicativa studia i numeri primi, la fattorizzazione degli interi e le proprietà delle funzioni aritmetiche, tra le quali è fondamentale la funzione \(\pi (x)\), che conta il numero dei primi minori o uguali a \(x\). Un risultato fondamentale della teoria moltiplicativa è il Teorema dei numeri primi, che descrive il comportamento asintotico della distribuzione dei numeri primi:
\[ \lim_{x \to \infty}\frac {\pi (x)\ln x}{x}=1 \]Un problema fondamentale della teoria additiva è il seguente: esprimere un intero positivo \(n\) come somma di elementi di un insieme di interi
\[ X = \{x_{1},x_{2}, \cdots x_{n},\cdots\} \]dove gli \(x_{i}\) possono essere numeri particolari come i numeri primi, i numeri quadrati, i cubi, ecc. Ogni rappresentazione possibile viene chiamata una partizione.
Un problema classico, ancora non risolto, è la famosa congettura di Goldbach, la quale afferma che ogni numero positivo pari può essere espresso come somma di due numeri primi. Un altro esempio è la congettura di Waring, secondo la quale, per ogni fissato numero naturale \(k\), esiste un intero positivo \(g\) tale che ogni intero positivo può essere rappresentato come somma di al massimo \(g\) potenze con esponente \(k\).
I primi risultati della teoria additiva dei numeri sono dovuti soprattutto a Fermat ed Eulero. In particolare Eulero studiò il problema di scomporre un intero positivo come somma di un certo numero di interi positivi. Egli dimostrò diversi teoremi mediante l’utilizzo delle funzioni generatrici o serie formali. Il vantaggio delle serie deriva dalla seguente semplice proprietà:
La moltiplicazione di due potenze si trasforma nella somma degli esponenti. Al contrario nella teoria moltiplicativa dei numeri vengono utilizzate le serie di Dirichlet \(\sum\limits_{k=1}^{\infty}\dfrac{a_{n}}{n^{s}}\), nelle quali per avere il prodotto si utilizza la relazione
\[ n^{s}\cdot m^{s}=(nm)^{s} \]2) Le partizioni di un intero
Definiamo partizione di un numero intero positivo \(n\) una rappresentazione di \(n\) come somma di interi positivi, chiamati parti della partizione. Sono ammesse ripetizioni e l’ordine non è importante; non ci sono limiti al numero degli elementi della partizione. La funzione di partizione di un numero \(n\) viene indicata con \(p(n)\). Poniamo inoltre \(p(0)=1\).
Esempio 2.1
Abbiamo \(p(6)=11\) poichè:
Per studiare l’andamento della funzione \(p(n)\) al crescere di \(n\) vedere questo link all’OEIS Foundation.
Imponendo delle specifiche condizioni sulle parti, possiamo definire altre funzioni di partizioni:
- \(p_{m}(n)\): numero di partizioni in parti minori o uguali a \(m\)
- \(p_{d}(n)\): numero di partizioni in parti distinte
- \(p_{o}(n)\): numero di partizioni in parti dispari
Esempio 2.2
\[ \begin{array}{l} p_{3}(6)=7 \\ p_{d}(8)= 6 \\ p_{o}(8)=6 \\ p_{o}(5)=3 \\ \end{array} \]Una partizione può essere rappresentata graficamente mediante i diagrammi di Ferrer. Ad esempio due partizioni del numero 25 sono le seguenti:
Le due partizioni di \(25\) illustrate nella figura precedente si dicono coniugate, in quanto una è la trasposta dell’altra, ovvero è ottenuta dall’altra per riflessione lungo la diagonale.
Una partizione che coincide con la sua coniugata si dice auto-coniugata. Due esempi di partizioni auto-coniugate sono le seguenti:
Mediante i diagrammi di Ferrer possono essere dimostrati diversi teoremi interessanti.
Teorema 2.1
Il numero di partizioni di \(n\) in \(m\) parti è uguale al numero di partizioni di \(n\) in parti in cui il massimo valore è \(m\).
Dimostrazione
Basta osservare che se nel diagramma di Ferrer di una partizione scambiamo le righe e le colonne, otteniamo una corrispondenza biunivoca fra i due tipi di partizioni del teorema.
Con ragionamento simile si può dimostrare il seguente teorema:
Teorema 2.2
Il numero di partizioni di \(n\) in al massimo \(m\) parti è uguale al numero di partizioni di \(n\) in parti che non superano \(m\).
Teorema 2.3
Il numero delle partizioni auto-coniugate di \(n\) è uguale al numero delle partizioni di \(n\) in parti dispari distinte.
Suggerimento
Per dimostrare questo teorema, stabilire una corrispondenza biunivoca fra i due tipi di partizioni. Dal diagramma di Ferrer della partizione auto-coniugata, unire i puntini che si trovano sui successivi angoli retti. Oppure fare il procedimento inverso se si parte da una partizione in parti dispari distinte.
Ad esempio alla partizione auto-coniugata \(15=6+3+3+1+1+1\) del numero \(15\) corrisponde la partizione in parti dispari e distinte \(15=11+3+1\).
Esempio 2.3
Per il numero \(6\) le partizioni in parti dispari sono le seguenti:
Di queste solo la \(5+1\) è costituita da parti dispari distinte. A questa corrisponde la partizione auto-coniugata \(3+2+1\).
3) Funzioni generatrici
Chiamiamo funzione generatrice di una successione di numeri \(\{a_{n}\}\), un’espressione del tipo
\[ \sum\limits_{k=0}^{\infty}a_{k}x^{k} \]dove i coefficienti \(a_{n}\) sono numeri interi e il simbolo \(x\) è una indeterminata cui non viene assegnato alcun valore numerico. Le funzioni generatrici sono un modo di rappresentare una successione di numeri mediante la corrispondenza:
\[ \{a_{0},a_{1}, \cdots, a_{n,\cdots} \} \leftrightarrow \sum\limits_{k=0}^{\infty}a_{k}x^{k} \]Nello studio delle funzioni generatrici in genere si trascurano gli aspetti relativi alla convergenza delle serie. In questo caso la funzione generatrice viene anche chiamata serie formale.
3.1) L’algebra delle serie formali
Due funzioni generatrici \( A(x) = \sum\limits_{n=0}^{\infty}a_{n}x^{n}\) e \(B(x) = \sum\limits_{n=0}^{\infty}b_{n}x^{n}\) sono equivalenti se \(a_{n}=b_{n}\) per ogni valore di \(n\).
Nell’insieme delle funzioni generatrici possiamo definire definire le seguenti operazioni di somma e prodotto:
\[ \begin{array}{l} A(x) + B(x)= \sum\limits_{n=0}^{\infty}(a_{n}+b_{n})x^{n} \\ \\ A(x)B(x) = \sum\limits_{n=0}^{\infty}c_{n}x^{n} \quad \text{dove } c_{n}=\sum\limits_{k=0}^{n}a_{k}b_{n-k} \end{array} \]Esercizio 3.1
Date \(3\) serie formali \(A,B,C\) (omettiamo l’indeterminata \(x\) per semplicità) dimostrare le seguenti relazioni:
L’insieme delle serie formali con le due operazioni sopra definite ha una struttura algebrica di anello, che può essere indicata con il simbolo \(\mathbb{Z}^{\mathbb{N}}(+,.)\). L’elemento zero è rappresentato dalla successione \((0,0,0, \cdots)\), mentre l’unità moltiplicativa è la successione \((1,0,0, \cdots)\).
Bisogna tenere presente comunque che le serie formali hanno diverse limitazioni. In alcuni casi è necessario considerare anche la convergenza delle funzioni generatrici.
Esercizio 3.2
Dimostrare che l’anello delle serie formali di potenze è un dominio di integrità, cioè non possiede divisori dello zero:
Esercizio 3.3 – Legge di cancellazione
Se \(A(x) \neq 0\) allora
Due funzioni generatrici \(A(x),B(x)\) si dicono reciproche se risulta \(A(x)B(x)=1\). La funzione \(B(x)\) si chiama l’inversa di \(A(x)\).
Esercizio 3.4
Dimostrare che la funzione generatrice inversa di \(A(x)\) esiste se e solo se \(a_{0} \neq 0\).
Esempio 3.1
La funzione generatrice inversa della \(A(x)=\sum\limits_{n=0}^{\infty}x^{n}\) è la funzione \(B(x)=1-x\) in quanto
3.2) Prodotti infiniti come funzioni generatrici
Nello studio delle partizioni spesso le funzioni generatrici sono rappresentate con prodotti infiniti. Tra queste in particolare la funzione \(p(n)\) che studieremo nel prossimo paragrafo.
Ricordiamo brevemente alcune definizioni.
Definizione 3.1
Data una successione di numeri reali \(\{u_{0}, u_{1}, \cdots \}\) non nulli, definiamo il prodotto parziale di ordine \(n\): \(\prod\limits_{i=0}^{n} u_{i}=u_{0}u_{1} \cdots u_{n}\). Se tale prodotto parziale tende ad un valore finito diverso da zero, questo limite è il valore del prodotto infinito
e il prodotto infinito si dice convergente. Se il limite vale zero allora si dice che il prodotto infinito diverge a zero. Se non converge ad un limite definito, il prodotto infinito si dice oscillante.
In alcuni problemi è conveniente cambiare notazione e scrivere \(u_{n}=1+a_{n}\). Con questa notazione la definizione diventa:
Esercizio 3.5
\[ \begin{array}{l} \prod\limits_{n=2}^{\infty}\left(1-\frac{1}{n^{2}}\right)=\frac{1}{2} \\ \prod\limits_{n=1}^{\infty}\left(1+\frac{1}{n}\right)=\infty \\ \end{array} \]Teorema 3.1
\[ 1+x+x^{2}+x^{3}+ \cdots = (1+x)(1+x^{2})(1+x^{4})(1+x^{8})\cdots \]Dimostrazione
Poniamo \(K=(1+x)(1+x^{2})(1+x^{4})\cdots\). Moltiplicando per \((1-x)\) abbiamo:
Poiché sappiamo che \((1-x)(1+x+x^{2}+ \cdots)=1\), ne deriva che \(K=1+x+x^{2}+ \cdots\).
Il significato del teorema precedente è che ogni intero positivo può essere espresso in modo univoco come somma di potenze di \(2\).
Teorema 3.2
Se \(n \ge 1\), allora
Dimostrazione
La funzione generatrice rappresentata dal seguente prodotto infinito
conta il numero di partizioni di \(n\) in parti distinte. D’altra parte abbiamo anche
\[ \begin{array}{l} (1+x)(1+x^{2})(1+x^{3})\cdots=\dfrac{1-x^{2}}{1-x} \dfrac{1-x^{4}}{1-x^{2}}\dfrac{1-x^{6}}{1-x^{3}}\cdots \\ = \dfrac{1}{(1-x)(1-x^{3})(1-x^{5})\cdots } \\ \end{array} \]L’ultimo prodotto infinito conta il numero di partizioni in parti dispari.
Esempio 3.2
\[ \begin{array}{l} 7 = 1+1+ \cdots 1=1+3+3=1+1+5=1+1+1+1+3 \\ 7= 1+2+4=1+6=2+5=3+4 \\ \end{array} \]4) Funzione generatrice per la funzione \(p(n)\)
Teorema 4.1
\[ \sum\limits_{n=0}^{\infty}p_{m}(n)x^{n}=\prod\limits_{k=1}^{m}\frac{1}{1-x^{k}} \quad |x| \lt 1 \]Cenni dimostrazione
Ricordiamo lo sviluppo delle seguenti \(m\) serie geometriche
con \(k=1,2 \cdots, m\). Poiché le serie convergono assolutamente, possiamo moltiplicare fra loro le \(m\) serie e disporre i termini a piacere, senza che cambi il risultato finale. Il prodotto complessivo dà come risultato una serie in cui il coefficiente davanti alla potenza \(x^{n}\) corrisponde al numero \(p_{m}(n)\) delle partizioni in parti che non superano \(m\). Possiamo quindi scrivere
\[ A_{m}(x)=\frac{1}{(1-x)(1-x^{2})\cdots(1-x^{m})}= \sum\limits_{n=0}^{\infty}p_{m}(n)x^{n} \]Teorema 4.2 – Eulero
\[ \prod\limits_{n=1}^{\infty}\frac{1}{1-x^{n}}=\sum\limits_{n=0}^{\infty}p(n)x^{n} \]Dimostrazione
La dimostrazione può essere completata a partire dal teorema precedente, osservando che \(p_{m}(n) \le p(n)\) e inoltre
Esercizio 4.1
\[ \sum\limits_{n=0}^{\infty}p_{o}(n)x^{n}= \prod\limits_{n=1}^{\infty}\frac{1}{1-x^{2n-1}} \]Esercizio 4.2
\[ \sum\limits_{n=0}^{\infty}p_{d}(n)x^{n}= \prod\limits_{n=1}^{\infty}(1+x^{n}) \]5) I numeri pentagonali e il teorema di Eulero
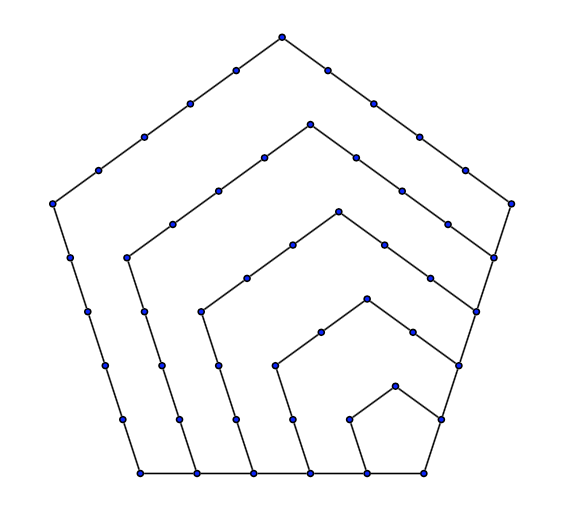
Definizione 5.1 – I numeri pentagonali
I seguenti numeri \(\omega(n)\) e \(\omega(-n)\) sono chiamati numeri pentagonali:
Fanno parte dell’insieme dei numeri figurati o poligonali. Possono infatti essere rappresentati con delle palline disposte a formare i lati di pentagoni.
I primi numeri pentagonali sono: 1, 5, 12, 22, 35, 51.
Tra i teoremi dimostrati da Eulero, ricordiamo in particolare il seguente:
Teorema 5.1 – Teorema pentagonale di Eulero
\[ \prod\limits_{k=1}^{\infty}(1-x^{k})=\sum\limits_{n=-\infty}^{\infty}(-1)^{n}x^{\dfrac{n(3n-1)}{2}} \]La dimostrazione del teorema è abbastanza lunga, anche se non eccessivamente complessa. Vedere ad esempio [1].
6) Formula ricorsiva di Eulero per la funzione \(p(n)\)
Eulero ha dimostrato la seguente formula ricorsiva, utile per il calcolo della funzione \(p(n)\).
Teorema 6.1 – Eulero
\[ \begin{array}{l} p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7) \\ + p(n-12)+p(n-15)- \cdots \\ = \sum\limits_{k=1}^{\infty}(-1)^{k+1}[p(n-\omega(k))+p(n-\omega(-k))] \end{array} \]Dimostrazione
Mediante i teoremi 4.2 e 5.1 possiamo scrivere
Il coefficiente di \(x^{n}\) a destra è uguale a zero, se \(n \ge1\). Quindi svolgendo i calcoli a sinistra e uguagliando i coefficienti otteniamo la formula di Eulero.
La formula di Eulero è utile per calcolare il valore della funzione \(p(n)\). Lo stesso Eulero riuscì a calcolare \(p(n)\) almeno fino a \(n=69\), mentre MacMahon(1850-1929) riuscì a calcolare il seguente valore:
\[ p(200)= 3.972.999.029.388 \]In seguito, mediante l’utilizzo di computer sempre più potenti, si è arrivati fino a \(p(2000)\) e oltre. Tuttavia, per numeri molto grandi il metodo non è più efficiente.
Esempio 6.1
Calcolare il valore di \(p(7)\) mediante la formula ricorsiva di Eulero.
Eulero dimostrò anche una formula simile per la funzione \(\sigma(n)\), somma dei divisori positivi di un numero naturale positivo \(n\).
Teorema 6.2 – Eulero
Se \(n \ge 1\) non è un numero pentagonale, allora
Se \(n =\dfrac{3k^{2} \pm k}{2}\) è un numero pentagonale, allora
\[ \begin{array}{l} \sigma(n)=(-1)^{k-1}n +\sigma(n-1)+\sigma(n-2)-\sigma(n-5)-\sigma(n-7) + \cdots \\ \end{array} \]Per una dimostrazione vedere [3].
7) Formula di Rademacher
Molti problemi relativi alla funzione \(p(n)\) rimangono tuttora aperti. Un problema molto importante è lo studio del comportamento asintotico della funzione \(p(n)\) al crescere di \(n\). Oltre ai contributi iniziali di Eulero, risultati importanti sono stati ottenuti da Hardy, Ramanujan e Rademacher.
Per illustrare la famosa formula di Hardy-Ramanujan-Rademacher ricordiamo prima la definizione della funzione di Dedekind:
La formula di Hardy-Ramanujan-Rademacher è la seguente:
\[ p(n)=\frac{1}{\pi \sqrt{2}}\sum\limits_{k=1}^{\infty}A_{k}(n)\sqrt{k}\frac{d}{dn}\left(\frac{\sinh \left(\frac{\pi}{k}\sqrt{\frac{2}{3}(n-\frac{1}{24})}\right)}{\sqrt{n-\frac{1}{24}}} \right) \]dove
\[ A_{k}(n)= \sum\limits_{0\le h \lt k;(h,k)=1}{}e^{\pi i s(h,k)-\frac{2\pi inh}{k}} \]La dimostrazione di questa formula è lunga e complessa. Per le proprietà della funzione di Dedekind e per una dimostrazione della formula vedere [2].
La formula di Hardy-Ramanujan-Rademacher è una formula esatta che ha permesso di calcolare il valore \(p(n)\) per grandi valori di \(n\). Ad esempio, Fredrik Johannson[4] è riuscito a calcolare \(p(10^{20})\), un numero enorme di 11.140.086.260 cifre.
Se prendiamo solo il primo termine dell’espansione, otteniamo la seguente formula per il comportamento asintotico:
\[ p(n) \sim \frac{1}{4n\sqrt{3}} e^{\pi \sqrt{\frac{2n}{3}}} \quad (n \to \infty) \]La formula precedente mostra che la crescita della funzione \(p(n)\) è sub-esponenziale. Il numero di cifre decimali di \(p(n)\) è approssimativamente uguale a \(\sqrt{n}\).
Conclusione
Lo studio della funzione di partizione iniziato con Eulero ha occupato in seguito i migliori matematici: Legendre, Gauss, Jacobi e molti altri. Nel secolo scorso importanti sviluppi sono stati raggiunti grazie al matematico inglese Hardy e soprattutto al matematico indiano Ramanujan. È tuttora uno dei settori della teoria dei numeri di maggiore interesse, sia per la sua importanza nella matematica pura, sia per alcune sue importanti applicazioni in altri campi, come la probabilità e la fisica quantistica.
Bibliografia
[1] Niven-Zuckerman-Montgomery – An introduction to the Theory of Numbers (Wiley)
[2] T. Apostol – Modular Functions and Dirichlet Series in Number Theory (Springer-Verlag)
[3] R. Remmert – Classical Topics in Complex Function Theory (Springer)
[4] Fredrik Johansson – Efficient implementation of the Hardy-Ramanujan-Rademacher formula (arXiv.org)
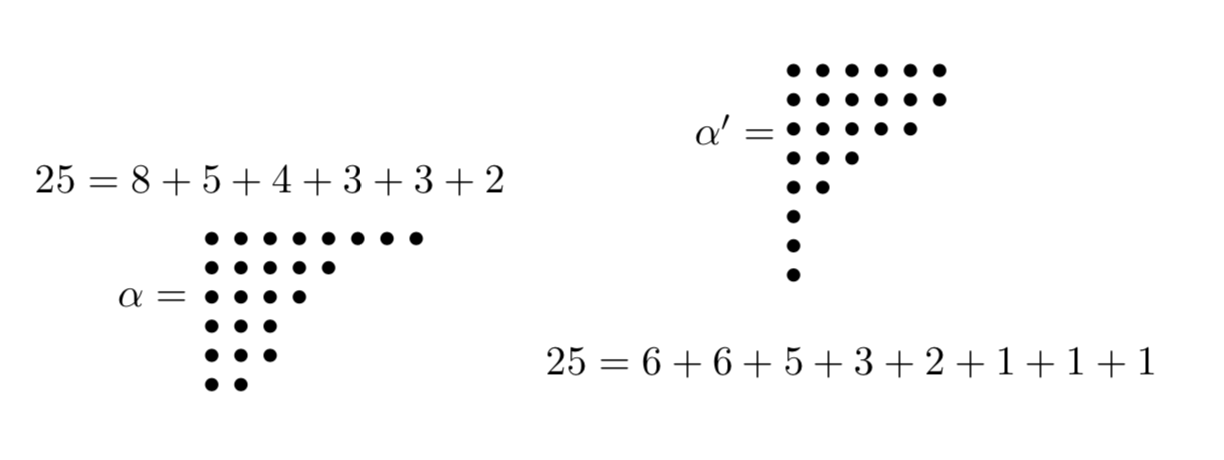
1 commento
Paolo · 9 Marzo 2024 alle 5:43 AM
Articolo ben fatto e chiaro , nonostante la difficoltà dell’ argomento . Complimenti